The Discrepancy
of Three Permutations

[October, 2012] DIMACS researcher
Alantha Newman and graduate student Aleksandar Nikolov
discovered a counterexample to a long-standing a conjecture by
Jozsef Beck (
Beck’s “Three
Permutations Conjecture” (c. 1982) states that when the set
system is derived from three permutations, the discrepancy of
the set system is a constant. The analogous result is true for
the set system based on two permutations, and there is a
simple, well-known proof demonstrating that fact.
Newman and
Nikolov showed that this well studied conjecture is false for
three permutations by providing a counterexample. For any positive
integer n =3k
, they exhibited three permutations whose
corresponding set system has discrepancy 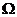 (log(n)).
(log(n)).
Professor Joel
Spencer (NYU) stated Beck’s conjecture in his Ten Lectures on the
Probabilistic Method in 1987 and offered a $100 reward
for settling it. Newman and Nikolov are shown collecting this
bounty.
One
inspiration for Newman and Nikolov’s work was a paper by
Eisenbrand, Palvolgyi and Rothvoss (SODA 2010) that showed that
if Beck’s conjecture were true, then a well-studied linear
programming (LP) relaxation for bin packing would yield a
lower bound on the value of an optimal integer solution that
is within an additive constant of optimal. Newman and Nikolov’s result closes that
particular path to approximability of bin packing.
Subsequently,
in joint work with Ofer Neiman (then a postdoctoral researcher
at 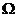 (log(n))
more bins than that of an optimal solution. Eisenbrand et al.
independently made this observation in an extended version of
their original paper, while Newman, Neiman and Nikolov
presented their work at the 2012 FOCS conference in
(log(n))
more bins than that of an optimal solution. Eisenbrand et al.
independently made this observation in an extended version of
their original paper, while Newman, Neiman and Nikolov
presented their work at the 2012 FOCS conference in
