Lecture # 5
| Instructor: Scot Drysdale |
June 28, 1996 |
Back to DIMACS Lectures
Homework Review
The intersection of two convex sets is a convex set. Select two points in the intersection.
Both are in the first set, so the segment joining them is in the first set by the
definitions of intersection and convexity. Similarly the segment joining the two points is in the second set. Therefore the segment joining them is in the intersection
by definition of intersection. All the regions in a Voronoi diagram are convex,
because they are intersections of n-1 half-planes (which are all convex).
You can't triangulate k collinear points, you would get a degenerate triangle as the
Delaunay Triangulation. However, if you then add a site off of the line its region
will be adjacent to the Voronoi region of every site on the line, so will be connected
to every point in the Delaunay Triangulation.
(Polyginal - parabola or Lou's polygon. The shape of the boundary of the Voronoi
region of the point off of the line in the example just given. )
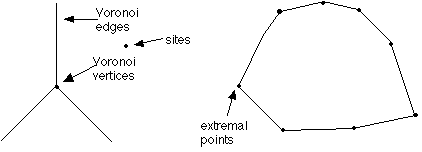
Vertices on the convex hull have infinite regions. This time, the points on the edges
of the convex hull between the extremal points are also included. Every point on
the convex hull, including points between the extremal points, has an infinite region.
Voronoi diagrams
CS Applications
- Knuth's Post-Office Problem
(or Nearest-Search Problem or Helicopter Rescue Problem)
- Closest Pair Problem
- All-Nearest-Neighbor Problems
- Euclidean Minimum Spanning Tree
- Largest Empty Circle Problem
(or Toxic Waste Dump Location Problem)
- Fixed-Radius Near Neighbor Problem
- All-Points-k- Nearest-Neighbor Problem
- Enumerating Interpoint Distances In Increasing Order
Page 173 for proof of size of diagram which refers you back to page 119
At most there are 3n - 6 ( really 3n - 3 - # of hull edges) Voronoi edges q(n)
2n - 4 Voronoi vertices
For an obtuse triangle the circumcenter is outside the region
For an acute triangle the circumcenter is inside the region
For a right triangle the circumcenter is on the edge
Euler's Formula
V + F - E = 2
Voronoi Diagrams in three-dimensions are used in Crystallography.
If Crystals start growing at same
time, grow at same
rate. (constant rate)
See slides A
1, A2, A3.
{x| dc (p,x) = dc(p,x)}
If crystals grow at some constant rate, but start at different
times. Starting time becomes an additive weight
. See slide B
1, B2.
Separators:
{x| dc(p,x) + w(p) = dc(q,x) + w(q)}
This can be arranged:
d(p,x) - d(q,x) = C + w(q) - w(p)
which shows that the shape of the "bisector" curves is a hyperbola.
What if crystals start at the same time
, but grow at different constant weights?
Multiplicutively weighted Voronoi Diagram. See slide C
1, C2, C3.
sep(p,q) = { x | dc(p,x)/ wp = dc(q,x)/ wq}
In this case the separator is a circle, which encloses the lighter-weight point but
is not centered at it.
Crystal (or Grain Growth) Models
- Johnson & Mehl (1939) - All sites with same growth rate, simultaneous or sequential
nucleation. These correspond to standard and additively weighted Voronoi diagrams,
respectively.
- Tamemura & Hasegawa (1980) - Territories of animals of equal strength. Similar models
to JM.
- Bülow-Olsen, Sakevile-Hamilton, & Hutchings (1984) - Colonies of clover. Uses same
growth rate assumption, so same models.
These models (standard and additively weighted) are O(n log n) algorithms to compute
them. (Shamos, Guibas & Stolfi, Fortune,...
- Frost & Thompson (1987, 1988) - Many different growth models, including multiplicatively
weighted. Use standard multiplicatively weighted diagram, but note it is not an
accurate model.
Multiplicatively weighted diagram studied by Aurenhammer & Edelsbrunner. O(n2) size and time, because regions can be disconnected.
The Multiplicative model is not
an accurate model of crystal growth. Distances measured in straight lines
through other
crystals.
Crystals cannot grow through areas that have already crystallized.
Should grow "around" slower growing crystals.
Treat other crystals as obstacles
.
Regions in multiplicatively weighted diagrams can be disconnected but clearly crystals
can not grow this way. Shaudt and Drysdale studied this. The separators are sometimes
part of circles, but can be much more complicated curves (e.g. logarithmic spirals).
What would it mean to be a Voronoi diagrams for line segments? or for polygons? Examples:
territorial waters for islands (each island gets the part of the ocean closer to
it than to other islands, within the 200-mile limit), sprinklers watering plants,
parking in Princeton
Robots - segments are walls and obstacles -- compute shortest distances to see if
robot can fit through and throw out any edges where the robot won't fit. Then analyze
the graph theory problem and see if you can get from start to finish. This can be
done in n log n time.
Homework 4
p. 192-193, 5.5.6. [1]
2. The Delaunay Triangulation has many useful properties. Here is another property
which it may or may not have: is it the minimum weight triangulation? That is,
if you add up the lengths of all edges in the Delaunay triangulation the sum of these
lengths be the smallest of all possible ways to triangulate the points? (Try figuring
this out for 4 points first.)
Informational:
http://www.supercomp.org/sc96/education --- To apply for funding to attend Supercomputing
96 in Pittsburg in Nov.
workshops on web
visualization
modeling
basic internet
by July 8 deadline
Mailto: dimacs-www@dimacs.rutgers.edu
Last modified: October 3, 1996

