
DIMACS/DIMATIA/Renyi Working Group on Extremal Combinatorics
Working Group Meetings:
- First
Meeting
- Dates: April 10 - 16, 2003
Location: Alfred Renyi Institute, Budapest, Hungary
- Second Meeting
- Dates: October 18 - 20, 2004
Location: DIMACS Center, CoRE Building, Rutgers University, Piscataway, NJ
- Third Meeting
- Dates: July 30 - 31, 2005
Location: Prague, Czech Republic
- Organizers:
- Gyula Katona, Alfred Renyi Institute, ohkatona@renyi.hu
The Rényi Institute Home Page
DIMACS/DIMATIA/Renyi Tripartite Partnership
Working Group Agenda:
This working group will concentrate on two general topics, extremal
graph theory and extremal problems arising from combinatorial search
and testing.
Extremal graph theory ([9, 34]) deals with
graphs satisfying specified constraints and optimizing some criterion.
We plan to investigate jointly a number of specific questions of
current research interest in this field, which has played a fundamental
role in the history of graph theory.
The generalized matching problem is to find many vertex-disjoint
copies of a fixed graph in a large graph. A corresponding extremal
graph theory notion was developed for certain fixed graphs and very
recently extended for all possible fixed graphs by Komlós [28].
The working group will collaborate on identifying the precise extremal
graphs in connection with this notion.
In general, we shall be interested in Turán-type extremal
problems. Here, a family L of sample graphs is fixed and we consider
various conditions on a graph on n vertices that does not contain
any graph in L as a subgraph (not necessarily induced). The most
famous such problem asks for the maximum number of edges ext(n,L) of
a graph G on n vertices that does not have any subgraph in
L. Turán solved this problem if L consists of the complete
graph Kp+1 and asked the same question for other cases where L
consists of a single graph. His goal was not so much to determine the
extremal number of edges as to discover some important new phenomena
by solving the problem for different cases. Surprisingly enough, some
very simple cases of this problem remain open, e.g., the case of the
cube Q8. Erdös and Simonovits [18] gave an
upper bound for ext(n,Q8) that they conjectured to be sharp, but
this conjecture remains unsettled and we will investigate it. Even
open is the conjecture that ext(n,Q8)/n3/2 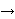
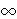 . Simonovits
[35] showed how some old methods can be
used to solve new Turán-type extremal problems, for instance the
determination of ext(n,P) where P is the Peterson graph. We shall
try to make use of similar ideas. Let us say that a graph has property
Bp,t if one cannot delete t-1 vertices from it to get a
p-colorable graph. A generalization of the Turán-type problem is
to find the maximum number of edges of a graph of n vertices that
contains no graph of L and has property Bp,t. This type of
question has been of interest since the work in [33].
More generally of interest is the same question where
property Bp,t is replaced by a condition that is called
in the literature a ``chromatic condition'' (see [35])
and we shall study Turán-type problems under
chromatic conditions.
. Simonovits
[35] showed how some old methods can be
used to solve new Turán-type extremal problems, for instance the
determination of ext(n,P) where P is the Peterson graph. We shall
try to make use of similar ideas. Let us say that a graph has property
Bp,t if one cannot delete t-1 vertices from it to get a
p-colorable graph. A generalization of the Turán-type problem is
to find the maximum number of edges of a graph of n vertices that
contains no graph of L and has property Bp,t. This type of
question has been of interest since the work in [33].
More generally of interest is the same question where
property Bp,t is replaced by a condition that is called
in the literature a ``chromatic condition'' (see [35])
and we shall study Turán-type problems under
chromatic conditions.
The Peterson graph is a special case of the Kneser graph, which is
defined as follows. Given a set A of a elements and an integer b
< a/2, define the Kneser graph, Z(a,b) to be the graph whose
vertices are the b-tuples of A and so that two of these b-tuples
are joined by an edge if and only if they are disjoint. The Peterson
graph is Z(5,2). The Kneser graph Z(a,b) can be colored in p =
a-2b+2 colors. It was a longstanding conjecture of Kneser and a deep
theorem of Lovász [31] (proved in a slightly simpler way
by Bárány [7]) that this number actually gives the
chromatic number. Recently, a unique combinatorial proof of Kneser's
conjecture was presented by Ji\v{r}í Matou\v{s}ek (DIMATIA) at
the DIMACS-DIMATIA workshop ``Homonolo'' in November 2000.
Matou\v{s}ek derived this result from Tucker's combinatorial lemma on
labeling the vertices of special triangulations of the octahedral
ball. By specializing a proof of Tucker's lemma, he obtained a
self-contained, purely combinatorial proof of Kneser's conjecture. It
remains an open problem, which we plan to investigate, to find the
minimum number p(a,b) of vertices that one can delete from the
Kneser graph to get an a-2b+1-chromatic graph, and similarly for
edges. Generalizations of Kneser's conjecture are still open for
n-tuple colorings. In such a coloring, each vertex x is assigned a
set C(x) of n colors in such a way that if x and y are
adjacent, then C(x) and C(y) are disjoint. These colorings can be
viewed as homomorphisms into Kneser graphs. We shall investigate an
old conjecture of Stahl [36] giving the smallest number of
colors in an n-tuple coloring of the Kneser graph (see also
[22]). This problem relates to the work of the Working
Group on Graph Coloring and Generalizations which will investigate
generalizations of n-tuple colorings called set colorings. The
Kneser graph is defined by subsets of a finite set. Many problems of
extremal graph theory are interesting in the more general setting of
extremal set theory or extremal hypergraph theory. (See for example
[16, 17, 15, 24].) As time permits, the
group will extend its work to these more general contexts.
An interesting
problem is to find the
minimum degree in a graph of n vertices that guarantees that the
graph will have the Peterson graph as a subgraph.
More generally, we
ask for the maximum value dex(n,L) of the minimum degree 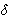 >(G)
of a graph G of n vertices that has no graph in family L as a
subgraph. It is easy to see that dex(n,L) < (2/n)ext(n,L). As
observed in [35], the upper bound is almost
achieved in many interesting cases, and we shall try to identify
conditions under which this is true.
>(G)
of a graph G of n vertices that has no graph in family L as a
subgraph. It is easy to see that dex(n,L) < (2/n)ext(n,L). As
observed in [35], the upper bound is almost
achieved in many interesting cases, and we shall try to identify
conditions under which this is true.
In approaching problems in extremal graph theory, two of the main
tools we shall use are the so-called Regularity Lemma of Szemerédi and
the Blow-up Lemma that was developed by Komlós, Sárközy and Szemerédi
[29]. For surveys about these tools, see
[27, 30].
This working group will also be concerned with several classes of
combinatorial search and testing problems. In one such problem, a
sequential test procedure, optimal with respect to an appropriate
performance criterion, is to be designed to identify a single item
from among a set of items, and the single item of interest is
``distinguished'' in some specific way recognizable by the tests. For
example, we may be performing diagnostic tests to identify a faulty
component within a system of components. If the system is monitored
continuously for failure, it is reasonable to assume that there is a
single faulty component present at the instant of system failure.
Katona [25, 26] has investigated the specific variant of
this problem in which there are constraints on the maximum number of
items which can be included in any test, a situation corresponding to
the case that the diagnostic device has some physical capacity
associated with it. He has also investigated various models in which
test results can be unreliable, obtaining (for both reliable and
unreliable frameworks) bounds on the maximum number of tests required
given that the goal is to minimize this quantity. We shall
investigate a number of variants of the search problem, such as the
case in which there are multiple diagnostic devices operating in
parallel, and when we focus on the performance criterion of minimum
average number of tests under a probability model imposed on the
individual items for being the single distinguished one. Work of
Abrahams [1] is relevant here. We plan to work on
performance bounds for minimum-average-number-of-tests problems in
which there are constraints on the individual test sizes. We will
also work on a number of other problem variants, both for reliable and
unreliable test models, particularly variants involving
linearly and partially ordered constraints on the items.
The working group will also investigate the related theory and
algorithms of combinatorial group testing (see [14]), with
emphasis on connections to coding theory and combinatorial
design. These topics are also of interest to the Working Group on
Algebraic and Geometric Methods in Combinatorics. To identify all
positive cases in a large population of items, group testing proceeds
by grouping the items into subsets, testing if a subset contains at
least one positive item, and then identifying all positive items
through iteration of group tests. The theory of group testing arose
via testing millions of World War II military draftees for syphilis
[13] and it is very relevant to schemes for large-scale
blood testing for viruses such as HIV. Group testing also arises in
connection with the mapping of genomes (see, e.g.,
[5, 6, 10, 19, 32]).
Here, we have a long list of molecular sequences, form a library of
subsequences (clones), and test whether or not a particular sequence
(a probe) appears in the library by testing to see which clones it
appears in. Because clone libraries can be huge, we do this by pooling
the clones into groups. Group testing is also relevant to the
identification of defective products and has found application in
satellite communications (see [12]). We will
investigate these various applications of group testing. Among the
specific questions we will explore are questions dealing with
two-stage group testing. Here, the goal of the first stage is to
identify a small subset of the items being tested that is sure to
contain all the positive items. Some preliminary work in this area is
contained in the papers
[8, 11, 21] and we shall
investigate it further, with emphasis on the problem of finding
designs that achieve some of the bounds obtained in [21].
We shall also investigate problems involving testing properties of
evolving objects. These problems can be formulated as
determining whether a function f has property P or is
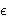 -far from any function with property P. A property testing
algorithm is given a sample of the value of f on instances drawn
according to some distribution, and, in some cases, it is also allowed
to query f on instances of its choice. The concept is defined by
Goldreich, Goldwasser and Ron [23]. The function
f, viewed as an object itself, can be of combinatorial, geometric or
algebraic nature. For instance f may describe a graph by assigning
an edge/non-edge value to every pair of points. Applications of
property testing range from the theory of learning to the theory of
probabilistically checkable proofs. Practical applications include
testing the hyper-link graph of the Internet and testing of
clusterings (related to data mining) [2]. Thus far all
property tests are designed to work with static objects even though
in reality the studied object (e.g., the hyper-link graph of the
Internet) can be constantly changing. In this new line of research we
will investigate efficient methods for testing changing objects and
will seek to determine the frequency with which we have to draw samples if we
want to keep the computed information up to date. For additional
relevant work, see [3, 4, 20].
-far from any function with property P. A property testing
algorithm is given a sample of the value of f on instances drawn
according to some distribution, and, in some cases, it is also allowed
to query f on instances of its choice. The concept is defined by
Goldreich, Goldwasser and Ron [23]. The function
f, viewed as an object itself, can be of combinatorial, geometric or
algebraic nature. For instance f may describe a graph by assigning
an edge/non-edge value to every pair of points. Applications of
property testing range from the theory of learning to the theory of
probabilistically checkable proofs. Practical applications include
testing the hyper-link graph of the Internet and testing of
clusterings (related to data mining) [2]. Thus far all
property tests are designed to work with static objects even though
in reality the studied object (e.g., the hyper-link graph of the
Internet) can be constantly changing. In this new line of research we
will investigate efficient methods for testing changing objects and
will seek to determine the frequency with which we have to draw samples if we
want to keep the computed information up to date. For additional
relevant work, see [3, 4, 20].
[1] Abrahams, J., ``Parallelized Huffman and Hu-Tucker
Searching,'' IEEE Trans. on Information Theory, 40, (1994)
508-510
[2] Alon, N., Dar, S., Parnas, M., and Ron, D. ``Testing of
Clustering,'' FOCS 2000, 2000, 240-250
[3] Alon, N., Fischer, E., Krivelevich, M., and
Szegedy, M., ``Efficient Testing of Large Graphs,'' FOCS
1999, 1999, 656-666
[4] Alon, N., Krivelevich, M., Newman, I., and Szegedy, M.
``Regular Languages are Testable with a Constant Number of
Queries,'' SIAM J. Comput., 30, (2000), 1842-1862.
[5] Balding, D.J., and Torney, D.C., ``Optimal
Pooling Designs with Error Detection,''
J. Comb. Theory, A74, (1996), 131-140.
[6] Balding, D.J., and Torney, D.C., ``The Design
of Pooling Experiments for Screening a Clone Map,'' Fungal
Genetics and Biology, 21, (1997), 302-307.
[7] Bárány, I., ``A Short Proof of Kneser's
Conjecture,'' J. Comb. Th., A25, (1978), 325-326.
[8] Berger, T., and Mandell, J.W., ``Bounds on the
Efficiency of Two-stage Group Testing,'' preprint, Cornell University,
1998.
[9] Bollobás, B., Extremal Graph Theory,
Academic Press, London, 1978.
[10] Bruno, W.J., Balding, D.J., Knill,
E.H., Bruce, D., Whittaker, C., Doggett, N., Stallings, R., and
Torney, D.C., ``Design of Efficient Pooling Experiments,''
Genomics, 26, (1995), 21-30.
[11] Chee, Y.M., Colbourn, C.J., and Ling,
A.C.H., ``Weakly Union-free Twofold Triple Systems,'' Annals
Combinatorics, 1, (1997), 215-225.
[12] Colbourn, C.J., Dinitz, J.H., and
Stinson, D.R., ``Applications of Combinatorial Design to
Communications, Cryptography, and Networking,''
http://www.emba.uvm.edu/~dinitz/preprints.html
[13] Dorfman, R., ``The Detection of Defective Members
of a Large Population,'' Annals of Math. Stat., 14,
(1943), 436-440.
[14] Du, D-Z, and Hwang, F.K., Combinatorial Group
Testing and its Applications, 2nd ed., World Scientific, Singapore,
2000.
[15] Enomoto, H., and Katona, G., ``Pairs of Disjoint
q-element Subsets Far from Each Other,'' Electronic
J. Combin., 8, (2001).
[16] Erdös, P., Frankl, P, and Katona, G.,
``Intersecting Sperner Families and their Convex Hulls,''
Combinatorica, 4, (1984), 21-34.
[17] Erdös, P., Frankl, P, and Katona, G.,
``Extremal Hypergraph Problems and Convex Hulls,''
Combinatorica,, 5, (1985), 11-26.
[18] Erdös, P., and Simonovits, M., ``Some
Extremal Problems in Graph Theory,'' in P. Erdös, et al. (eds.),
Combinatorial Theory and its Applications, North-Holland,
Amsterdam, 1970, 377-390.
[19] Farach, M., Kannan, S., Knill, E., and
Muthukrishnan, S., ``Group Testing Problems with Sequences in
Experimental Molecular Biology,'' Proc. of Sequences '97 (Conference on
Compression and Complexity of Sequences, Positano, Salerno, Italy),
1997.
[20] Fischer, E., and Newman, I., ``Testing of Matrix Properties,'' Proceedings of The 33rd STOC, 2001.
[21] Frankl, P., and Füredi, Z., ``A New
Extremal Property of Steiner Triple Systems,'' Discrete Math.,
48, (1984), 205-212.
[22] Frankl, P., and Füredi, Z., ``Extremal
Problems Concerning Kneser Graphs,'' J. Comb. Th., B40,
(1986), 270-284.
[23] Goldreich, O., Goldwasser, S., and Ron, D. ``Property Testing
and its Connection to Learning and Approximation,''
JACM,, 45, (1998), 653-750.
[24] Idzik, A., Katona, G., and Vohra, R., ``Intersecting Balanced
Families of Sets,'' J. Combin. Theory, A93, (2001),
281-291.
[25] Katona, G., ``Rényi and the Combinatorial Search Problems,'' Studia. Sci. Math. Hungar., 26, (1991), 363-378.
[26] Katona, G., ``Search with Small Sets in Presence of a
Liar,'' J. Statistical Planning Infer., to appear.
[27] Komlós, J., ``The Blow-up Lemma (Survey),''
Combinatorics, Probability and Computing, 8, (1999),
161-176.
[28] Komlós, J., ``Tiling Turán Theorems,''
Combinatorica, 20, (2000), 203-218.
[29] Komlós, J., Sárközy, G.N., and Szemerédi, E.,
``Blow-up Lemma,''
Combinatorica, 17, (1997), 109-123.
[30] Komlós, J., and Simonovits, M.,
``Szemerédi's Regularity Lemma and its Applications in Graph Theory,''
in D. Miklós, V. T. Sós, T. Szonyi (eds.),
Combinatorics, Paul Erdös is Eighty (Volume 2), Bolyai
Society Mathematical Studies, Budapest, 1996, 295-352.
(See also DIMACS Technical Report 96-10, 1996.)
[31] Lovász, L., ``Kneser's Conjecture, Chromatic
Number, and Homotopy,'' J. Comb. Th., A25, (1978),
319-324.
[32] Ngo, H.Q., and Du, D-Z., ``A Survey on Combinatorial
Group Testing Algorithms with Applications to DNA Library Screening,''
in D-Z. Du, P.M. Pardalos, P.M., and J. Wang, J. (eds.), Discrete
Mathematical Problems with Medical Applications, DIMACS Series, 55,
American Mathematical Society, Providence, RI, 2000.
[33] Simonovits, M., ``Extremal Graph Problems with
Symmetric Extremal Graphs, Additional Chromatic Conditions,''
Discrete Math., 7, (1974), 349-376.
[34] Simonovits, M., ``Extremal Graph Theory,'' in
L. Beineke and R. Wilson (eds.), Selected Topics in Graph
Theory, Academic Press, London, 1983, 161-200.
[35] Simonovits, M., ``How to Solve an Extremal
Problem?'' in R. Graham, J. Kratochvíl, J. Nesetril, and F.S. Roberts
(eds.), Contemporary Trends in Discrete Mathematics, DIMACS
Series, Vol. 49, American Mathematical Society, Providence, RI, 1999,
283-305.
[36] Stahl, S., ``n-tuple Colorings and Associated
Graphs,'' J. Comb., Th., 20, (1976), 185-203.
 Working Group Index
Working Group Index
 DIMACS Homepage
DIMACS Homepage
Contacting the Center
Document last modified on May 3, 2005.
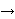
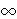 . Simonovits
[35] showed how some old methods can be
used to solve new Turán-type extremal problems, for instance the
determination of ext(n,P) where P is the Peterson graph. We shall
try to make use of similar ideas. Let us say that a graph has property
Bp,t if one cannot delete t-1 vertices from it to get a
p-colorable graph. A generalization of the Turán-type problem is
to find the maximum number of edges of a graph of n vertices that
contains no graph of L and has property Bp,t. This type of
question has been of interest since the work in [33].
More generally of interest is the same question where
property Bp,t is replaced by a condition that is called
in the literature a ``chromatic condition'' (see [35])
and we shall study Turán-type problems under
chromatic conditions.
. Simonovits
[35] showed how some old methods can be
used to solve new Turán-type extremal problems, for instance the
determination of ext(n,P) where P is the Peterson graph. We shall
try to make use of similar ideas. Let us say that a graph has property
Bp,t if one cannot delete t-1 vertices from it to get a
p-colorable graph. A generalization of the Turán-type problem is
to find the maximum number of edges of a graph of n vertices that
contains no graph of L and has property Bp,t. This type of
question has been of interest since the work in [33].
More generally of interest is the same question where
property Bp,t is replaced by a condition that is called
in the literature a ``chromatic condition'' (see [35])
and we shall study Turán-type problems under
chromatic conditions.
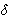 >(G)
of a graph G of n vertices that has no graph in family L as a
subgraph. It is easy to see that dex(n,L) < (2/n)ext(n,L). As
observed in [35], the upper bound is almost
achieved in many interesting cases, and we shall try to identify
conditions under which this is true.
>(G)
of a graph G of n vertices that has no graph in family L as a
subgraph. It is easy to see that dex(n,L) < (2/n)ext(n,L). As
observed in [35], the upper bound is almost
achieved in many interesting cases, and we shall try to identify
conditions under which this is true. 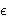 -far from any function with property P. A property testing
algorithm is given a sample of the value of f on instances drawn
according to some distribution, and, in some cases, it is also allowed
to query f on instances of its choice. The concept is defined by
Goldreich, Goldwasser and Ron [23]. The function
f, viewed as an object itself, can be of combinatorial, geometric or
algebraic nature. For instance f may describe a graph by assigning
an edge/non-edge value to every pair of points. Applications of
property testing range from the theory of learning to the theory of
probabilistically checkable proofs. Practical applications include
testing the hyper-link graph of the Internet and testing of
clusterings (related to data mining) [2]. Thus far all
property tests are designed to work with static objects even though
in reality the studied object (e.g., the hyper-link graph of the
Internet) can be constantly changing. In this new line of research we
will investigate efficient methods for testing changing objects and
will seek to determine the frequency with which we have to draw samples if we
want to keep the computed information up to date. For additional
relevant work, see [3, 4, 20].
-far from any function with property P. A property testing
algorithm is given a sample of the value of f on instances drawn
according to some distribution, and, in some cases, it is also allowed
to query f on instances of its choice. The concept is defined by
Goldreich, Goldwasser and Ron [23]. The function
f, viewed as an object itself, can be of combinatorial, geometric or
algebraic nature. For instance f may describe a graph by assigning
an edge/non-edge value to every pair of points. Applications of
property testing range from the theory of learning to the theory of
probabilistically checkable proofs. Practical applications include
testing the hyper-link graph of the Internet and testing of
clusterings (related to data mining) [2]. Thus far all
property tests are designed to work with static objects even though
in reality the studied object (e.g., the hyper-link graph of the
Internet) can be constantly changing. In this new line of research we
will investigate efficient methods for testing changing objects and
will seek to determine the frequency with which we have to draw samples if we
want to keep the computed information up to date. For additional
relevant work, see [3, 4, 20].  Working Group Index
Working Group Index