Proof of Lemma 24
Considering the semantics of specification triples, it is sufficient to
prove for every positive formula ![]() with
with ![]() that for arbitrary s ,
that for arbitrary s ,
![]() follows from
follows from
![]() positive,
positive,
![]() and
and ![]() .We will prove this by induction on the structure of (positive)
.We will prove this by induction on the structure of (positive) ![]() .
We write
.
We write ![]() and
and ![]() .
.

First, assume that for some R : ![]() . Then:
. Then:

Now assume that for no R : ![]() ; in particular,
; in particular, ![]() . We want to prove that also in that case
. We want to prove that also in that case ![]() . So assume
. So assume ![]() , i.e.,
, i.e.,
![]() , and therefore
, and therefore
![]() . The only participant R' that can have
. The only participant R' that can have ![]() is B .
From
is B .
From ![]() and
and ![]() we see that
we see that ![]() , and so
, and so
![]() . Note further that
. Note further that ![]() . We now prove by induction on the structure of messages that
for all M :
. We now prove by induction on the structure of messages that
for all M :
If
,
,
and
,
then




Since ![]() ,
, ![]() and
and ![]() are also increase,
the proofs for
are also increase,
the proofs for ![]() ,
, ![]() ,
, ![]() and
and ![]() are analogous.
are analogous.
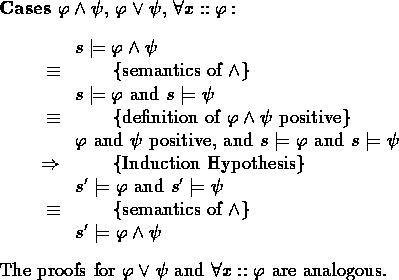
![]()
Proof of Lemma 28
The proof is analogous to the proof of Lemma 24.
According to the semantics of specification triples, it is sufficient to
prove for every formula ![]() in
in ![]() that for arbitrary s ,
that for arbitrary s ,
![]() follows from
follows from ![]() safe,
safe,
![]() and
and ![]() .For positive
.For positive ![]() Lemma 24 ensures that
Lemma 24 ensures that
![]() . For
. For ![]() (where
(where ![]() is positive)
we must prove that either
is positive)
we must prove that either
![]() is positive, or
is positive, or ![]() under the
assumptions mentioned.
We prove this by induction on the structure of (positive)
under the
assumptions mentioned.
We prove this by induction on the structure of (positive) ![]() .Before embarging on the induction, note that formulas of
each of the forms
.Before embarging on the induction, note that formulas of
each of the forms ![]() ,
, ![]() ,
, ![]() and
and ![]() are invariant under the mapping
are invariant under the mapping
![]() , so that we can skip them in the case
analysis.
, so that we can skip them in the case
analysis.



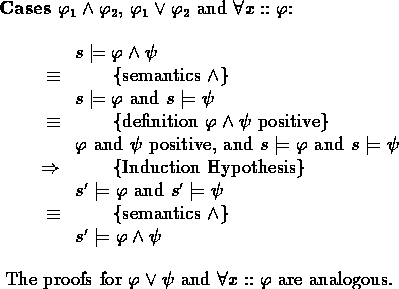
Finally, the postponed
Case
Observe that
![]() .
The first conjunct of this expression is positive, which is enough to prove our
claim. The second conjunct is not positive, hence we need to prove
.
The first conjunct of this expression is positive, which is enough to prove our
claim. The second conjunct is not positive, hence we need to prove
![]() separately.
separately.
According to the definition of ![]() , we can assume:
, we can assume:
We have to prove:For all
:
Let P andFor all
:

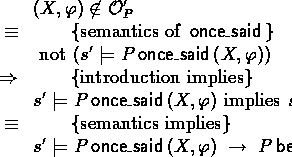
For ![]() , we first observe
that P=A (only the sender's
, we first observe
that P=A (only the sender's ![]() set has changed). We now prove
the following statement by induction on M :
set has changed). We now prove
the following statement by induction on M :
If,
,
,
and, then
.
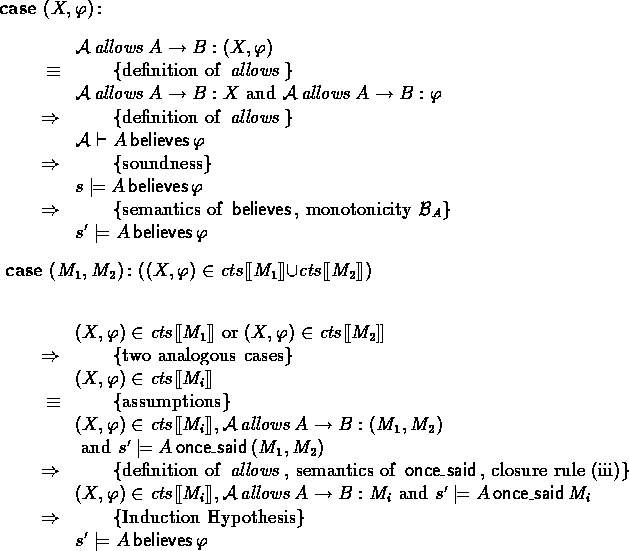

This proves by induction the claim
Ifwhich concludes Case,
,
,
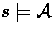
and, then
.
![]()