

Next: Semantics of formulas
Up: A semantics for BAN
Previous: Rectification of formulas
We view the environment as a system consisting of a finite collection of
principals.
We define for a principal P
a local state
as a tuple 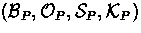 , with the intuitive
interpretation:
, with the intuitive
interpretation:
-
 , the set of formulas that P currently believes;
, the set of formulas that P currently believes;
-
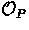 , the set of (sub-)messages P once said;
, the set of (sub-)messages P once said;
-
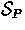 , the set of messages that P has seen so far;
, the set of messages that P has seen so far;
-
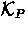 , the set of keys P possesses.
, the set of keys P possesses.
It is closed if it
satisfies the following (mutually defined) closure
properties, each of which corresponds directly to an axiom:
- 1.
- (Rationality)
Principals believe every theorem of the logic:
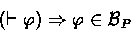
- 2.
- (Believing Modus Ponens)
Principals apply Modus Ponens in their beliefs:
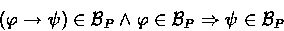
- 3.
- (Saying parts of a joint message)
If a principal said a combination of messages at a certain time, then that
principal said each of the messages as well:

The reverse does not hold, since the presence of a joint message in
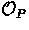 implies that both components were uttered (as a joint message)
at the same time;
implies that both components were uttered (as a joint message)
at the same time;
- 4.
- (Saying contents of an encrypted message)
If a principal said an encrypted message and believes the key is
good, then that principal said the contents of the encrypted message as
well:
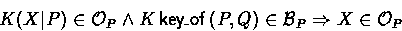
- 5.
- (Seeing parts of a joint message)
If a principal sees a joint message, that principal
sees each of the messages as well:
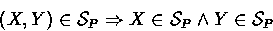
(Note that the reverse does not hold, since a joint message implies
utterance of its components at the same time, i.e., within the same
message.)
- 6.
- (Awareness)
If a principal sees a message, then that principal also believes
he sees it:
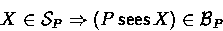
- 7.
- (Possessing keys of a seen key statement)
If a principal sees a key statement, then that principal possesses
the key mentioned:
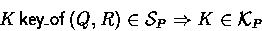
- 8.
- (Possessing believed keys)
If a principal believes that a certain key is a good key statement,
then that principal must possess that key as well:
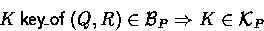
- 9.
- (Decryption)
If a principal P possesses a key K , and if P sees a message X
labeled with Q and encrypted with K , then P also sees X itself:
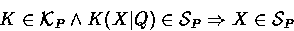
(Note that there is no closure property corresponding to
the axiom Good key ensures the utterer.)
The closure of a local state s is the least closed local
state s' such that  , where the
ordering is obtained by component-wise lifting of the set ordering.
Note that taking the closure only adds elements to
the sets involved, and leaves an already closed local
state unchanged.
, where the
ordering is obtained by component-wise lifting of the set ordering.
Note that taking the closure only adds elements to
the sets involved, and leaves an already closed local
state unchanged.
A global state is a mapping from principals to
local states (for each principal in the environment).
Global states are ordered by lifting the ordering on
local states.
The closure of a global state s , denoted by
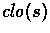 , is defined in the obvious way.
The unqualified term ``state'' will, from now on, mean a
closed global state.
, is defined in the obvious way.
The unqualified term ``state'' will, from now on, mean a
closed global state.
We consistently use the convention that for a state denoted by the
variable s its local state for principal P is
denoted by the tuple 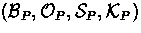 ,and likewise that for a state s'
its local state for principal P is
denoted by the tuple
,and likewise that for a state s'
its local state for principal P is
denoted by the tuple 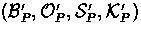



Next: Semantics of formulas
Up: A semantics for BAN
Previous: Rectification of formulas
![]()
![]()
![]() implies that both components were uttered (as a joint message)
at the same time;
implies that both components were uttered (as a joint message)
at the same time;
![]()
![]()
![]()
![]()
![]()
![]()
![]() , where the
ordering is obtained by component-wise lifting of the set ordering.
Note that taking the closure only adds elements to
the sets involved, and leaves an already closed local
state unchanged.
, where the
ordering is obtained by component-wise lifting of the set ordering.
Note that taking the closure only adds elements to
the sets involved, and leaves an already closed local
state unchanged.
![]() , is defined in the obvious way.
The unqualified term ``state'' will, from now on, mean a
closed global state.
, is defined in the obvious way.
The unqualified term ``state'' will, from now on, mean a
closed global state.
![]() ,and likewise that for a state s'
its local state for principal P is
denoted by the tuple
,and likewise that for a state s'
its local state for principal P is
denoted by the tuple ![]()