About Discrete Math
K-8 Leadership Program
Exploring Discrete Mathematics in the Classroom
2000 Institutes
What Is Discrete Mathematics?
- Because it is grounded in real-world problems, discrete mathematics
lends itself easily to implementing the recommendations of the
National Council of Teachers of Mathematics (NCTM) Standards.
- Because many discrete math problems are simply stated and have few
mathematical prerequisites, they can be introduced at all grade
levels, even with children who are not yet fluent readers.
EXAMPLE: How Many Colors?
At early elementary levels, children can color the regions on the first diagram below using different colors for adjacent regions. Eventually they can determine the minimum number of colors needed to do this and explain why this number is the minimum.By grade 8, they can apply such coloring techniques to solve problems which involve avoiding conflicts, such as scheduling committees or final exams, devising zoo habitats, and assigning channels to radio stations.
EXAMPLE: What's The Shortest Route?
At early elementary levels, children can explore diagrams laid out on the classroom floor using masking tape (see example below). Have the children place a number of buttons on each segment to represent its length, and ask them to look for the shortest route from SCHOOL to HOME by counting the buttons along various routes.
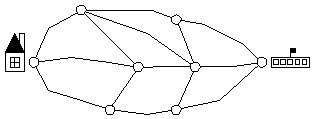
Problems involving "What's the shortest route?" can be incorporated throughout the curriculum: children can work with diagrams like this on paper (to reinforce arithmetic skills); can create their own diagrams (to reinforce measuring skills); and can solve problems based on road maps (to reinforce map-reading skills).
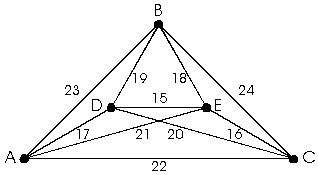
By grade 8, they can explore and solve more complex problems, like determining the shortest route for completing a set of errands, and can justify their solutions. For example, using the distances assigned to the lines on the diagram below, find the shortest route starting and ending at Point A, making stops at points B, C, D, and E.
| Home Page |