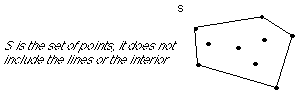Lecture # 1
| Instructor: Scot Drysdale |
June 24, 1996 |
Back to DIMACS Lectures
Text:
Computational Geometry in C
Joseph O'Rourke; Cambridge University Press, 1993
Chapter 3: Convex Hulls in Two Dimensions
What is Geometry?
Euclid's time it was a construction science.
Later some things proved not possible to construct. Emphasis changed to "what can
we prove" or "what is true" rather than "how can we construct these objects".
Descartes Cartesian coordinate geometry.
In 70's computer science discovered geometric problems
GIS (Geometric Information System) Maps on the web, data base that is geographic.
Preserving natural landscapes, natural resource areas. Computing from points, lines,segments.
Slide 1: cad layout - geometry intersection problem
Algorithms needed to find faster ways to test for intersections of rectangles (to
find where transistors are located on chips). Can't afford to test every rectangle
against every other rectangle (which would take proportional to n2 operations). Testing 1,000,000 rectangles at 1 microsecond per test would take 5
days. Better to take time proportional to n or n log n. If n = 1,000,000, then
n log n tests would only take 20 seconds at 1 microsecond per test (log here is base
2).
Slide 2: Space Shuttle
Designing 2 or 3 dimensional layouts. In CAD systems and graphics systems represent
surfaces by triangles.
Goals for the course will be to:
Learn how to compute geometric objects.
Take efficiency into account.
Topics to be covered:
- Convex hulls (chapter 3)
- Voronoi diagrams and Delaunay Triangulations (chapter 5) There are many alternate
names and applications for these Voronoi diagrams. Reference:
Okabe, A., Boots, B., Sugihara, K.. Spatial Tessellations: Concepts and Applications of Voronoi Diagrams,
John Wiley, Chichester, England, 1992.
- Art Gallery problems and visibility problems (Chapter 1)
Convex hulls (page 71-72) definitions:
Scot's definition of convex hull:
Take a plane and hammer in nails, stretch a big rubber band around the outside of
the nails and let it go. The convex hull is the rubber band and everything inside
it. Extremal points are the corner points touching the rubber band. We won't call
points on edges but not at corners extremal.
You want a computer program to print out a list of extremal points in counter-clock
wise order. It takes about the same amount of time to list them in order as to
list them as found.
| If there are 3 collinear points and the two end points are extremal points then the point lying between them may be considered an extremal point or it may be considered to not be an extremal point depending on the application. |
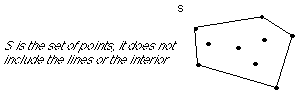 |
Mathematician's definitions of convex hulls:
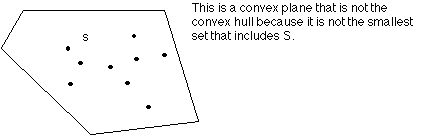
Convex hull CH(S) of a set S of n points in the plane is:
The smallest
convex set containing S. There exists no convex set C such that S is a subset of
C is a subset of CH(S)
The smallest area
set
The smallest perimeter
set
# 1,2,3 are the same with different ways of finding smallest
Intersection
of all
convex sets containing S.
Intersection of all half planes
containing S.
Why do we care about finding the smallest
set? Applications
Reasons why we might want to find the convex hull:
- finding the best fit line in a physics experiment - minimize the distance from any
point to the line by finding the convex hull of the set of data points as a first
step.
- Given a set of points if you want to find the diameter of a set of points. This takes
time proportional to n2. Being clever, you can use the rotating calipers' method to find the diameter. (the
calipers are always parallel lines and they stretch and shrink as needed). Keep track of each pair of points that calipers on opposite sides touch at the same
time, remember the longest distance. How many points will you touch? Given each of the n edges, there is one thing on
the opposite side so you are looking at 2n pairs. Can use the same approach to find
the width
of the set - minimum distance that the calipers can achieve.
- Sheep and goats problem -can you draw a straight line fence that will separate the
sheep from the goats? Take the convex hull of each set, if they do not intersect
then you can put in a fence. If they intersect, no
- Robotics problem - if the convex hulls don't run into each other than the robots won't
either.
Discussion Questions:
- How can you compute CH(S)
- What properties
of CH might be useful?
- What sort of geometric tests or operations does your algorithm use?
- How many
operations does it use? (Function of # points)
Regrouped - thoughts.
Properties: points with the max and min x,y points are extreme
(on the convex hull) How do you prove something is NOT on the convex hull? Use a
triangle to determine if something is inside.
How can you tell if 2 points form an edge of the convex hull? No points to the left
of the line (left is on the outside of the convex hull if you are an ant crawling
clockwise around the perimeter).
Left of
test, given 2 points you can test if a 3rd point is to the left, on, or to the right
of the line.
Mailto: dimacs-www@dimacs.rutgers.edu
Last modified: October 3, 1996