Lecture # 3
| Instructor: Scot Drysdale |
June 26, 1996 |
Back to DIMACS Lectures
Discussion
of the running time of the Rope Fence or Gift Wrap algorithm.
Suggested answers are:
- q(n2) this is a correct answer for the worse case when you have to do it n times because
all the points are on the hull
- q(hn) this is a correct answer and the better answer because you are giving a more
detailed answer.
- q(n) - this one was withdrawn
How many points are there on the hull? It depends on the shape of the hull.
- You expect q(log n) points on the hull of n points uniformly distributed in a polygon (no matter
how many sides).
- You expect q(3 n) points on the hull of n points uniformly distributed in a circle.
Santalos wrote a book on Integral Geometry, includes these facts.
Incremental algorithm
- Sort on X --- this takes q(n log n)
- Do incremental part after sorting completed --- q(n)
Add these together you get
q(n log n) + q(n) = q(n log n)
Homework Review
Problem 1:
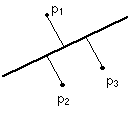
Take a set of points and find the best fit line using the convex hull.
Three points if arranged as in the figure will determine the best fit line. These points when arranged with the projection in the line of p1 located between the projections in the line of p2 and p3 will determine where the line has to be located. |
 |
So possible candidates for the best line are those determined by two consecutive points
on the CH of the points (that is, the endpoints of an edge) and the furthest point
away from them on the opposite side of the CH.
Finding a single candidate takes q(h) time. This because there are h points, take an edge there are (h-2) points left
to check. If we did this for all h edges on the hull we would take q(h) + q(h) + q(h) + ... + q(h) = O(h2) time (adding up h terms, one for each edge.) . Using the rotating calipers method
you can manage to do this in q(h).
Unimodality property of convex polygons - the distances from an edge of a polygon
to the vertices of the polygon increase to a maximum and then they decrease as you
move around the polygon.
Compute the hull it takes q(n log n) then in q(h) time you can find the line.
Problem 2:
 |
Start with 2 points, call it 0 , pick another point measure the angle,grow the wedge, as long as the sum of the angle measure is less than 180 the first point is on the hull. |
Graham's Scan
- the first (one of the first) published papers in computational geometry.
| Start by sorting the points in polar order around the leftmost point (lowest of the
leftmost in case of ties) and then connect them in order to find a polygon. Walk
around the perimeter, right turns are good and you keep the point as being on the
hull, left turns are bad and the point is not on the hull so you eliminate the point and back
up to repeat the previous test. In the figure, the extremal points are marked with
dots and the convex hull is the darker line. |
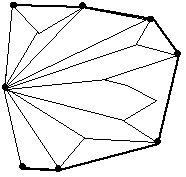 |
Given q(n log n) to sort the n points this will take no more than O(n2). (Each step you can back up at most n places.) But we can do better in our analysis.
You insert each point once and delete each point no more than once, this gives you
n points forward and n - h backwards. So it ends up being q(n).
Divide and Conquer
Sort a set of points by x-coordinate.
Split into left and right halves.
Find the convex hull of each side.
Find the lower mutual tangent line (line of support that touches the bottom most point
in each hull). This can be done by starting with a segment between the rightmost
point on the left side and the rightmost point on the right half and working down
(see Algorithm 3.9 in the text).
Do the same thing on the top so that you now have the upper mutual tangent line.
Eliminate all the points between these two lines.
q(h1 + h2) or just q(n)
T(n) = Time to compute CH of n points (once points are sorted
)
T(n) = 2T(n/2) + q(n)
= q(n log n)
How long to "conquer"? Construct a tree with one problem of size n at the top level,
2 problems of size n/2 at the second level, 4 problems of size n/4 at the third,
etc. Then adding up the total work done level by level:
c(n) = cn
1st 2 c (n/2) = cn
2nd 4 c (n/2) = cn
3rd 8 c (n/2) = cn
jth 2j c (n/2) = cn
|
 |
|
= c lgn n = q(n lg n) |
because there are lg n levels in the tree to get down to sets of size 1, which cannot
be further subdivided.
Back to the Quick Hull
algorithm.
Find the max and min x and y values.
Connect the quadrilateral
Throw out all the points in the interior
find the farthest point away from the segment and connect a triangle
throw out all the points in the interior of the each triangle
repeat if there are points c outside the triangle
Best
- original points are
the hull (all else inside) q(n) --- this is linear
Worst
- Each time all the points are outside of the triangle, and all on the same side
of the new vertex. The problem size reduces by only 1. This leads to the recurrence
relationship:
T(n) = T(n-1) + n = q(n2)
Average case
- points are uniformly distributed
. Then at each step of the recursion the points lie within a trapezoid:
At least half of the area of the trapezoid lies within the triangle, so we expect
at least half of the points to lie within the triangle, so they are eliminated. This
leads to:
T(n) = T(n1) + T(n2) + q(n)
n1 + n2 (1/2)n |
 |
The amount of work done at the top level is cn, at the next level cn/2, at the next
level cn/4, ... . Adding up this geometric series gives 2cn, so the total expected
work is Q(n).
Homework 3
Draw 3 points on a sheet of paper or in Sketchpad. Draw two points in the interior
of the triangle formed by the three points. Create the Voronoi diagram and Delaunay
triangulation of the five points. (You might want to try diagrams for 2 and 3 points
first.)
Some of the sites have bounded regions in the Voronoi diagram. Others have unbounded
regions. Give a characterization of sites that have unbounded regions and prove
it.
Describe how to create a Voronoi diagram on n points where one of the sites has degree
n-1.
Mailto: dimacs-www@dimacs.rutgers.edu
Last modified: October 3, 1996