
A Selection of Working Group Accomplishments: Working Group on Streaming Data Analysis and Mining I
A Windowed Data Stream Model for Detecting Patterns in
Streaming Data.
In many areas of application, the sheer volume of
data requires us to make a quick decision about it as it ``streams''
by. This is particularly true in applications of fraud detection in
telecommunications, in surveillance in homeland security, and in
financial transactions, as well as in astrophysics, environmental
modeling, etc. We have been working on methods to detect patterns in
streaming data. S. Muthukrishnan (Rutgers) and Mayur Datar (Stanford)
developed a unique ``windowed data stream model'' that is based on
observing a ``window'' of the last N observations. With storage
space less than the window size N, they studied the problem of
estimating the ``rarity'' of items in the window, a crucial problem in
telephone credit card fraud detection and anomaly detection in
counter-terrorism surveillance. They also studied the problem of
estimating the ``similarity'' between two data stream windows, an
important problem in sharing data between datasets obtained by
different agencies/companies, a vital problem in the homeland security
area. Dr. Muthukrishnan visited the NJ Office of Insurance Fraud in
the Division of Criminal Justice to discuss analogous problems they
are having. Muthukrishnan and Datar found novel, simple algorithms for
estimating rarity and similarity in this windowed situation.
Constructing the First Known Data Stream Algorithm for Estimating
Dominance of Multiple Signals.
Graham Cormode (University of
Warwick) and S. Muthukrishnan (Rutgers) considered streams of multiple
signals (i,ai,j) where the i's correspond to the domain, the
j's index the different signals and i,ai,j gives the value of the
j'th signal at point i. They addressed the problem of determining
the dominance norms over the multiple signals, in particular the
max-dominance norm defined as
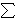 i maxj ai, j.
Besides finding
many applications, such as in estimating the ``worst case influence''
of multiple processes, for example in IP traffic analysis or
electrical grid monitoring, this norm is a natural measure: it
generalizes the notion of union of data streams and may be alternately
thought of as estimating the L1 norm of the upper envelope of multiple
signals. Cormode and Muthukrishnan constructed the first known data
stream algorithm for estimating max-dominance of multiple signals. The
algorithm is simple and implementable; its analysis relies on using
properties of stable random distributions with small parameter alpha,
which may be a technique of independent interest.
They also showed that other dominance norms -- min-dominance
sumiminjai,j,
count-dominance (|i|ai>bi|)
or relative-dominance (sumiai/max1,bi) --
are all impossible to estimate accurately with sublinear space.
i maxj ai, j.
Besides finding
many applications, such as in estimating the ``worst case influence''
of multiple processes, for example in IP traffic analysis or
electrical grid monitoring, this norm is a natural measure: it
generalizes the notion of union of data streams and may be alternately
thought of as estimating the L1 norm of the upper envelope of multiple
signals. Cormode and Muthukrishnan constructed the first known data
stream algorithm for estimating max-dominance of multiple signals. The
algorithm is simple and implementable; its analysis relies on using
properties of stable random distributions with small parameter alpha,
which may be a technique of independent interest.
They also showed that other dominance norms -- min-dominance
sumiminjai,j,
count-dominance (|i|ai>bi|)
or relative-dominance (sumiai/max1,bi) --
are all impossible to estimate accurately with sublinear space.
Space Lower Bounds for Distance Approximation in
the
Data Stream Model. Michael Saks (Rutgers) and Xiaodong Sun (Rutgers)
investigated the problem of approximating the distance between two
d-dimensional vectors x and y in the classical data
stream model. In this model, the 2d coordinates are presented as a
``stream''
of data in some arbitrary order, where each data item includes the
index
and value of some coordinate and a bit that identifies the vector
( x or y) to which it belongs. The goal is to minimize
the
amount of memory needed to approximate the distance.
For the case of Lp-distance with p 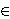 [1,2],
there were known good approximation algorithms that run in
polylogarithmic
space in d (here one assumes that each coordinate is an integer
with O(log d) bits).
Saks and Sun proved that they do not exist
for p>2. In particular,
they proved a nearly optimal approximation-space tradeoff of
approximating
$L^\infty$ distance of two vectors.
They showed that any randomized algorithm
that approximates $L^\infty$ distance of two length d vectors
within factor of $d^\delta$ requires $\Omega(d^{1-4\delta})$ space.
As a consequence they showed that for $p>2/(1-4\delta)$,
any randomized algorithm that approximate
Lp distance of two length d vectors within a factor
$d^{\delta}$
requires $\Omega(d^{1-\frac 2p-4\delta})$ space.
The data stream model has been recognized recently as an important
model, because it abstracts the problem of analyzing vast amounts
of data ``streaming'' into a collection point.
As for any model of computation, it is of interest
to draw a dividing line between things that are
efficiently computable in the model and things that are not.
Previously other researchers had shown that
approximating the distance of two vectors in this
model could be done efficiently for standard
Euclidean distance and L1 (Manhattan) distance.
These algorithmic techniques did not help for
the case of $L^\infty$ (max) distance. The work of Saks and Sun
demonstrated that this latter problem
is inherently unsolvable efficiently, provided a
striking contrast with the other two cases.
The lower bound follows from a lower bound on the two-party one-round
communication complexity of this problem. This lower bound
is proved using a combination of information theory and Fourier
analysis.
[1,2],
there were known good approximation algorithms that run in
polylogarithmic
space in d (here one assumes that each coordinate is an integer
with O(log d) bits).
Saks and Sun proved that they do not exist
for p>2. In particular,
they proved a nearly optimal approximation-space tradeoff of
approximating
$L^\infty$ distance of two vectors.
They showed that any randomized algorithm
that approximates $L^\infty$ distance of two length d vectors
within factor of $d^\delta$ requires $\Omega(d^{1-4\delta})$ space.
As a consequence they showed that for $p>2/(1-4\delta)$,
any randomized algorithm that approximate
Lp distance of two length d vectors within a factor
$d^{\delta}$
requires $\Omega(d^{1-\frac 2p-4\delta})$ space.
The data stream model has been recognized recently as an important
model, because it abstracts the problem of analyzing vast amounts
of data ``streaming'' into a collection point.
As for any model of computation, it is of interest
to draw a dividing line between things that are
efficiently computable in the model and things that are not.
Previously other researchers had shown that
approximating the distance of two vectors in this
model could be done efficiently for standard
Euclidean distance and L1 (Manhattan) distance.
These algorithmic techniques did not help for
the case of $L^\infty$ (max) distance. The work of Saks and Sun
demonstrated that this latter problem
is inherently unsolvable efficiently, provided a
striking contrast with the other two cases.
The lower bound follows from a lower bound on the two-party one-round
communication complexity of this problem. This lower bound
is proved using a combination of information theory and Fourier
analysis.
M. Saks and X. Sun, Space Lower Bounds for Distance Approximation in
the
Data Stream Model, Proceedings 34th Annual ACM Symposium on Theory
of Computing (STOC), 2002, 360-369.
A revised and expanded version has been submitted for journal
publication.
A Selection of Additional Achievements/Accomplishments
Brian Babcock, Mayur Datar, and Laidan O'Callaghan are
developing techniques for k-median clustering over "sliding
windows." Thus, a stream of data points is arriving, and the most
recent N points are considered "relevant", but memory is not
large enough to store N points. Their algorithm maintains a running
constant-approximate k-median clustering of the relevant points in
polylog space.
Adam Meyerson, Laidan O'Callaghan, and Serge Plotkin have a
Monte Carlo algorithm that produces a clustering that with
high-probability is approximately optimal under the k-median
measure of clustering. Lower bounds are produced on the running
time required and on the sizes of the samples that must be
clustered.
This material is based upon work supported by the National Science Foundation under Grant No. 0100921
 Index of Special Focus on Data Analysis and Mining
Index of Special Focus on Data Analysis and Mining
 DIMACS Homepage
DIMACS Homepage
Contacting the Center
Document last modified on April 29, 2003.
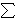 i maxj ai, j.
Besides finding
many applications, such as in estimating the ``worst case influence''
of multiple processes, for example in IP traffic analysis or
electrical grid monitoring, this norm is a natural measure: it
generalizes the notion of union of data streams and may be alternately
thought of as estimating the L1 norm of the upper envelope of multiple
signals. Cormode and Muthukrishnan constructed the first known data
stream algorithm for estimating max-dominance of multiple signals. The
algorithm is simple and implementable; its analysis relies on using
properties of stable random distributions with small parameter alpha,
which may be a technique of independent interest.
They also showed that other dominance norms -- min-dominance
sumiminjai,j,
count-dominance (|i|ai>bi|)
or relative-dominance (sumiai/max1,bi) --
are all impossible to estimate accurately with sublinear space.
i maxj ai, j.
Besides finding
many applications, such as in estimating the ``worst case influence''
of multiple processes, for example in IP traffic analysis or
electrical grid monitoring, this norm is a natural measure: it
generalizes the notion of union of data streams and may be alternately
thought of as estimating the L1 norm of the upper envelope of multiple
signals. Cormode and Muthukrishnan constructed the first known data
stream algorithm for estimating max-dominance of multiple signals. The
algorithm is simple and implementable; its analysis relies on using
properties of stable random distributions with small parameter alpha,
which may be a technique of independent interest.
They also showed that other dominance norms -- min-dominance
sumiminjai,j,
count-dominance (|i|ai>bi|)
or relative-dominance (sumiai/max1,bi) --
are all impossible to estimate accurately with sublinear space.

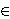 [1,2],
there were known good approximation algorithms that run in
polylogarithmic
space in d (here one assumes that each coordinate is an integer
with O(log d) bits).
Saks and Sun proved that they do not exist
for p>2. In particular,
they proved a nearly optimal approximation-space tradeoff of
approximating
$L^\infty$ distance of two vectors.
They showed that any randomized algorithm
that approximates $L^\infty$ distance of two length d vectors
within factor of $d^\delta$ requires $\Omega(d^{1-4\delta})$ space.
As a consequence they showed that for $p>2/(1-4\delta)$,
any randomized algorithm that approximate
Lp distance of two length d vectors within a factor
$d^{\delta}$
requires $\Omega(d^{1-\frac 2p-4\delta})$ space.
The data stream model has been recognized recently as an important
model, because it abstracts the problem of analyzing vast amounts
of data ``streaming'' into a collection point.
As for any model of computation, it is of interest
to draw a dividing line between things that are
efficiently computable in the model and things that are not.
Previously other researchers had shown that
approximating the distance of two vectors in this
model could be done efficiently for standard
Euclidean distance and L1 (Manhattan) distance.
These algorithmic techniques did not help for
the case of $L^\infty$ (max) distance. The work of Saks and Sun
demonstrated that this latter problem
is inherently unsolvable efficiently, provided a
striking contrast with the other two cases.
The lower bound follows from a lower bound on the two-party one-round
communication complexity of this problem. This lower bound
is proved using a combination of information theory and Fourier
analysis.
[1,2],
there were known good approximation algorithms that run in
polylogarithmic
space in d (here one assumes that each coordinate is an integer
with O(log d) bits).
Saks and Sun proved that they do not exist
for p>2. In particular,
they proved a nearly optimal approximation-space tradeoff of
approximating
$L^\infty$ distance of two vectors.
They showed that any randomized algorithm
that approximates $L^\infty$ distance of two length d vectors
within factor of $d^\delta$ requires $\Omega(d^{1-4\delta})$ space.
As a consequence they showed that for $p>2/(1-4\delta)$,
any randomized algorithm that approximate
Lp distance of two length d vectors within a factor
$d^{\delta}$
requires $\Omega(d^{1-\frac 2p-4\delta})$ space.
The data stream model has been recognized recently as an important
model, because it abstracts the problem of analyzing vast amounts
of data ``streaming'' into a collection point.
As for any model of computation, it is of interest
to draw a dividing line between things that are
efficiently computable in the model and things that are not.
Previously other researchers had shown that
approximating the distance of two vectors in this
model could be done efficiently for standard
Euclidean distance and L1 (Manhattan) distance.
These algorithmic techniques did not help for
the case of $L^\infty$ (max) distance. The work of Saks and Sun
demonstrated that this latter problem
is inherently unsolvable efficiently, provided a
striking contrast with the other two cases.
The lower bound follows from a lower bound on the two-party one-round
communication complexity of this problem. This lower bound
is proved using a combination of information theory and Fourier
analysis.
 Index of Special Focus on Data Analysis and Mining
Index of Special Focus on Data Analysis and Mining