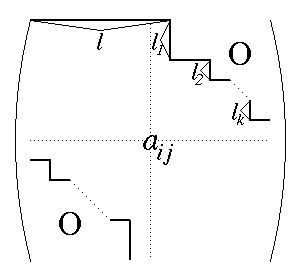
Let $G$ be a simple connected graph with $n$ vertices, let $\lambda_i(G)$ be the $i$th largest eigenvalue of $G$. This paper provides the following results:
1. If $\lambda_3(G)<0$, then the adjacency matrix of $G$, $A(G)$ is cogredient to the matrix:
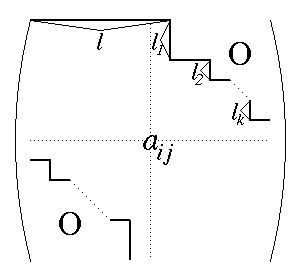
where $a_{ij}=1$ iff $i\ne j$ and $a_{ij}=0$ otherwise, and $$l_1+l_2+\ldots+l_k\le l.$$ Furthermore, if there exists an index $i$ such that $l_i > 1$, then $ G $ has the eigenvalue $-1$ with multiplicity at least $n-2r-1$, where $2r$ is the rank of $A(G^c)$.
2. $\lambda_3(G)<0 $ implies that $ \lambda_j(G)\ge -1$, $j=3,4,\ldots,n-r $, where $2r$ is the rank of the adjacency matrix of the complement of $G$, $2r \le n-1$.
DIMACS Home Page