Tim Ting Chen, University of Southern California
Title: Inferring Domain-Domain Interactions from Protein-Protein Interactions
Understanding protein-protein interactions is one of the most
important challenges in the post-genomic era. Behind protein-protein
interactions there are protein domains physically interacting with one
another to perform functions of proteins. Yeast 2-hybrid screens have
generated more than 6000 interactions between proteins of the yeast
Saccharomyces cerevisiae. This allows us to study the large-scale
conserved patterns of interactions between protein domains. We use
evolutionarily conserved domains defined in a protein-domain database
called Pfam, and apply the Maximum Likelihood Estimation method to
infer interacting domains that are consistent with the observed
protein-protein interactions. Using these interacting domains, we
predict about 100 novel yeast protein-protein interactions, among
which many proteins have either unknown function or no observed
interactions with other proteins. Our results can also be applied to
predict protein-protein interactions of other species.
(This is a joint research with Minghua Deng, Shipra Metah, and Fengzhu Sun.)
Dietmar Cieslik, University of Greifswald
Title: Steiner's Problem in Phylogenetic Spaces
A fundamental problem in many areas of classification is the
reconstruction of the evolutionary past. Trees are widely used to
represent evolutionary relationships. In biology, for example, the
dominant view of the evolution of life is that all existing organisms
are derived from some common ancestor and that a new species arises by
a splitting of one population into two or more populations that not do
not cross-breed, rather than by a mixing of two populations into one.
Here, the high level history of life is ideally organized and display
as tree. Trees may also be used to classify individuals of the same
species. In historical linguistics, trees have been used to represent
the evolution of language, while in the branch of philosophy known as
stemmatology, trees may represent the way in which difference versions
of a manuscript arose through successive copying. The principal of
maximum Parsimony involves the identification of a combinatorial
structure that requires the smallest number of evolutionary changes.
It is often said that this principle abides by Ockham's
razor1.
Steiner's Problem is the "Problem of shortest connectivity",
that means given a finite set of points in a metric space (X, ρ),
search for a network interconnecting these points with minimal length.
This shortest network must be a tree and is called a Steiner Minimal
Tree (SMT). It may contain vertices different from the points, which
are to be connected. Such points are called Steiner points. We will
consider the problem of reconstruction of phylogenetic trees in the
our sense of shortest connectivity. To do this we introduce so-called
Phylogenetic spaces. These are metric spaces whose points are
arbitrary words generated by characters (or letters; symbols) from
some (finite) alphabet, and the metric measuring "sameness" of the
words which is generated by a cost measure on the
characters2.
The "central dogma" is:
A most parsimonious tree is a SMT in a desired chosen phylogenetic space.
The following problems will be discussed:
Miklós Csürös, Université de Montréal &
Aleksandar Milosavljevic, Baylor College of Medicine
Title: Comparative physical mapping using Pooled Genomic Indexing
1. Introduction. Pooled Genomic Indexing (PGI) is a novel method for
comparative physical mapping of clones onto known macromolecular
sequences. PGI indexes genomes of new organisms using the already
assembled genomic sequences of humans and other organisms. An
application of the basic PGI method to BAC clone mapping is
illustrated in Figure 1. PGI first pools arrayed BAC clones, then
shotgun sequences the pools at an appropriate coverage, and uses this
information to map individual BACs onto homologous sequences of a
related organism. Specifically, shotgun reads from the pools provide a
set of short (cca. 500 base pair long) random subsequences of the
unknown clone sequences (100-200 thousand base pair long). The reads
are then individually compared to reference sequences, using standard
sequence alignment techniques [1] to find homologies. A set of
homologies with close alignments in a reference sequence forms an
index to the clone(s) identified by the set of pools the reads
originate from. The indexes constitute a comparative physical map that
enables targeted sequencing of regions of highest biomedical
importance. Protocols for BAC pooling and shotgun sequencing of BAC
pools have been originally developed at the Baylor Human Genome
Sequencing Center in support of Clone-Array Pooled Shotgun Sequencing
(CAPSS) [2]. In contrast to PGI, CAPSS deconvolutes using fragment
overlaps to produce an assembled sequence, and thus requires higher
read coverage.
2. Pooling designs In addition to the simple arrayed pooling design
shown in Figure 1, more sophisticated non-adaptive group testing
methods [3] and clone-pool designs [4] can also be used with PGI. In
general, a clone may be included in more than two pools, and the
design does not necessarily correspond to an array layout. A homology
between a reference sequence and a clone is detected by close local
alignments between the reference sequence and shotgun reads
originating from the pools the clone is included in. The success of
indexing in the PGI method depends on the possibility of deconvoluting
the local alignments. In the case of a simple array design, homology
between a clone and a reference sequence is recognized by finding
alignments with fragments from one row and one column pool. It may
happen, however, that more than one clone are homologous to the same
region in a reference sequence (and therefore to each other). This is
the case if the clones overlap, contain similar genes, or contain
similar repeat sequences. Appropriate pooling designs [5, 6] can
ensure that not only individual clones, but clone sets of a certain
size are also uniquely identifiable by the pools they are included in.
Concentrating on a given index, classical probabilistic and
combinatorial group testing results apply to PGI, the index being the
analogue of a defective item in group testing terminology. Using
standard techniques of modeling random shotgun reads [7], we analyze
the probability of successful indexing for clones or clone sets, as
well as probabilities for false positives and other aspects of index
deconvolution. In contrast to a classical probabilistic testing
problem, PGI generates many indexes at a time, and the probabilities
of detecting homologies are determined by a controllable parameter in
the experiment, namely, the number of random shotgun reads.
Ding-Zhu Du, University of Minnesota
Title: Some New Constructions for Pooling Designs
The non-adaptive and error-tolerance pooling design
has gained an important application in DNA library
screening. We propose two new classes of this type of
pooling designs. These designs induce a construction of
a binary code with minimum Hamming distance of at least
2d+2.
This work is joint with Hung Q. Ngo.
Dannie Durand, Carnegie Mellon
Title: Validating gene clusters
Large scale gene duplication, the duplication of whole genomes and
subchromosomal regions, is a major force driving the evolution of
genetic functional innovation. Whole genome duplications are widely
believed to have played an important role in the evolution of the
maize, yeast and vertebrate genomes. Two or more linked clusters of
similar genes found in distinct regions on the same genome are often
presented as evidence of large scale duplication. However, as the
gene order and the gene complement of duplicated regions diverge
progressively due to insertions, deletions and rearrangements, it
becomes increasingly difficult to determine whether observed
similarities in local genomic structure are indeed remnants of common
ancestral gene order, or are merely coincidences. In this talk, I
present combinatorial and graph theoretic approaches to validating
gene clusters in comparative genomics.
Wen-Lian Hsu, Academia Sinica, Taipei, Taiwan, ROC &
Wei-Fu Lu, National Chiao Tung University, Hsin-chu, Taiwan, ROC
Title: A Clustering Algorithm for Testing Interval Graphs on Noisy Data
An important problem in DNA sequence analysis is to reassemble the
clone fragments to determine the structure of the entire molecule. The
idea is to describe each clone by some fingerprinting method. One such
method is probe hybridization, in which a short molecule called a
probe is used to bind (or hybridize) to the clone, the hybridization
data is then used to determine the overlap relationships of the clones
[1,5,10]. An error-free version of this problem can be modeled as an
interval graph recognition problem, where an interval graph is the
intersection graph of a collection of intervals (we shall use the term
interval and clone interchangeably in this abstract). Several linear
time algorithms have been designed to recognize interval graphs
[2,7,8]. However, since the data collected from laboratories almost
surely contain some errors, traditional recognition algorithms can
hardly be applied directly. It should be noted that there is no
obvious way to modify existing linear time interval graph test
algorithms to incorporate small errors in the data. That is, a single
error could cause the construction of the interval model to
halt. Several related approximation problems have also been shown to
be NP-hard [3,4,9,12].
To cope with this dilemma we propose a clustering algorithm that is
robust enough to discover certain types of input errors and to correct
them automatically. The errors considered here include false positives
(two originally non-overlapping intervals appear to overlap in the
data) and false negatives (two originally overlapping intervals appear
not to overlap in the data). The kind of error tolerant behavior
considered here are similar in nature to algorithms for voice
recognition or character recognition problems. Thus, it would be
difficult to guarantee that a given error tolerant algorithm always
produces a desirable solution; the result should be justified through
benchmark data and real life experiences. Our clustering algorithm has
the following features:
1. the algorithm will assemble the clones correctly when the data is
error-free.
2. in case the error rate is small (say, less than 10%) the test can
likely detect and automatically correct the false positives and false
negatives.
3. the test can accommodate some probabilistic assumptions about the
overlapping relationships.
4. by providing confidence score on the endpoints, the test will also
identify those parts of the data that are problematic, thus allowing
biologists to perform further experiments to clean up the data.
The idea of our error-tolerant algorithm is based on an algorithm
modified from a linear time test of interval graphs [7]. In the
algorithm, we get rid of the rigid structure such as PQ-trees [2] or
sophisticated ordering [7,8] that are powerless in dealing with
errors. Instead, we make use of a certain robust local structural
property to weed out false positives that are remotely related to the
current interval first. We then use this structural property to treat
local false positives, false negatives and to order the neighboring
clones. Such a structural property has to do with the overlapping
relationships among neighbors of an interval, which are described
below.
Assume we have an interval model for a given graph. For each interval
u, consider those intervals that strictly overlap u (do not contain u
nor are contained in u). Divide these intervals into two parts: A(u),
those passing through the left endpoint of u and B(u), those passing
through the right endpoint of u. The adjacency relationships between
intervals in these two sets satisfy a monotone triangular (MT)
property. In case the data contains a reasonable small percentage of
error (say 10%), it would still be possible to recover such a MT
property approximately. This phenomenon has been illustrated in our
result for testing the consecutive ones property of a (0,1)-matrix
under noise [11].
In order to accommodate false positives and false negatives in the
data, some clustering and thresholding techniques are
adopted. Although it is hard to guarantee that the algorithm produces
an approximate solution model within a certain percentage of error,
the experimental result on synthetic data is extremely convincing that
the algorithm should give satisfactory interval models in most cases.
Our techniques are quite flexible in that we can even accommodate the
case where the overlapping relationships are expressed in terms of
probabilistic values instead of the deterministic zeros and ones. At
the end, the algorithm could provide the confidence score for each
endpoint position. This could prompt biologists to redo some
experiment to clean up the noisy part.
Another important feature of our algorithm is that, although it
utilizes the local monotone triangular property, the error-correcting
effect can be quite global. When it appears that a clone creates a
disrupting behavior for its neighbors, this clone could be deleted
from further consideration. Such a measure is installed to prevent
possible disastrous result.
In summary, we have modified previous rigid algorithms for testing
interval graphs into one that can accommodate clustering techniques as
well as probabilistic assumptions, and produces satisfactory
approximate interval models for most synthetic data.
References:
1. F. Alizadeh, R.M. Karp, L.E. Newberg, and D.K. Weisser, (1995) Physical mapping
of chromosomes: a combinatorial problem in molecular biology.
Algorithmica, 13, 52-76.
2. K.S. Booth and G.S. Lueker, Testing for the Consecutive Ones Property, Interval
Graphs, and Graph Planarity Using PQ-tree Algorithms, J. Comput Syst.
Sci. 13, 1976, 335-379.
3. M.C. Golumbic, Algorithmic Graph Theory and Perfect Graphs, Academic Press,
New York, 1980.
4. M.C. Golumbic, H. Kaplan and R. Shamir, On the Complexity of DNA Physical
Mapping, Advances in Applied Mathematics 15, 1994, 251-261
5. M.T. Hallett, (1996) An Integrated Complexity Analysis of Problems from
Computational Biology. Ph.D. thesis. Department of Computer Science,
University of Victoria, Victoria, BC, Canada.
6. W.L. Hsu, A simple test for the consecutive ones property, Journal of
Algorithms 42, 1-16, 2002.
7. W.L. Hsu, A simple test for interval graphs, LNCS 657, 1992, 11-16.
8. W.L. Hsu and T. H. Ma, Substitution Decomposition on Chordal Graphs and
Applications, LNCS 557, 1991, 52-60.
9. H Kaplan, R Shamir, and R.E Tarjan, (1994) Tractability of parameterized
completion problems on chordal and interval graphs: minimum fill-in and physical
mapping. In FOCS'94.
10. J.D Kececioglu, (1991) Exact and Approximation Algorithms for DNA Sequence
Reconstruction. Ph.D. thesis. Technical report TR 91-26, Department of Computer
Science, University of Arizona.
11. W.F. Lu and W.L. Hsu, A Test for the Consecutive Ones Property on Noisy Data,
submitted to Journal of Computational Biology.
12. M. Yannakakis, Computing the Minimum Fill-In is NP-Complete, SIAM J. Alg.
Disc. Meth 2, 1981.
Frank Hwang, National Chiao Tong University
Title: Random pooling designs with various structures
Typically, there are two ways to construct pooling designs, one through
using some mathematical structure, and the other through randomness.
Recently, several constructions which combine both the structure and
randomness elements have been proposed. These include the random k-set
design, the distinct random k-set design, the random k-size design and
several designs by Macula. We will first update the best formulas to compute
the success probabilities of identifying a positive clone with the first
three models.
For the basic 1-stage Macula's design with parameters (n,k,d), Macula gave
an approximate algorithm to identify positive clones from this design, and
an analysis of the success probability. For d=2, which is the focus of
Macula's analysis, we will propose a new method which provably identifies
more positive clones, but the analysis is much more difficult. So far, we
have exact result only when the number of positive clones is at most 3.
Macula also gave a 2-stage design and an approximate formula with 2
summation signs, and a further approximation in explicit form. We will gave
an exact formula also with 2 summation signs, and an approximation in
explicit form, which is more accurate than Macula's explicit approximation.
The purpose of the approximation is to facilitate the finding of optimal
design parameters.
Finally, we will provide some numerical comparisons between the various
random models, and between Macula's analysis and our new analysis.
F.K. Hwang and Y.C. Liu
Title: Error-tolerant Pool Designs with Inhibitors
Pooling designs are used in clone library screening to efficiently
identify positive clones from negative clones. Mathematically, a
pooling design is just a nonadaptive group testing scheme which has
been extensively studied in the literature. In some applications,
there is a third category of clones called ''inhibitors'' whose effect
is to neutralize positive clones. Namely, the presence of an
inhibitor in a pool dictates a negative outcome even though positive
clones are present. Sequential group testing schemes, which can be
modified to 3-stage schemes, have been proposed for the inhibitor
model, but it is unknown whether a pooling design (a one-stage scheme)
exists. Another open question raised in the literature is whether the
inhibitor model can treat unreliable pool outcomes. In this paper we
give a pool-design (one-stage), as well as a 2-stage scheme for the
inhibitor model with unreliable outcomes. The number of pools required
by our schemes are very comparable to the 3-stage scheme.
Esther Lamken, Caltech
Title: Two applications of designs in biology
In this talk, I will describe two applications of combinatorial designs in
biology. The first application uses ideas from finite geometry and design
theory to help design pooling experiments. The second application extends
work of Sengupta and Tompa. I will describe how ideas from design theory
and cryptography can be used to deal with the problem of multiple step
failure in the manufacture of DNA microarrays at Affymetrix.
Wen-Hsiung Li, Department of Ecology & Evolution, University of Chicago
Title: Methods for Aligning Long Genomic Sequences
Many eukaryotic genomes will soon be completely or near completely
sequenced. An extremely challenging problem is how to align genomic
sequences, which is usually the first step in comparative
analysis. Alignment of genomic sequences is much more difficult than
alignment of protein sequences or DNA sequences of protein coding
regions because (1) the large demand of computer time and memory
space, (2) the sequences often have been scrambled by insertion of
transosable elements, translocation, and inversion, and (3) the
existence of highly divergent regions. Some methods for aligning
genomic sequences will be presented.
Alan C.H. Ling, Charles J. Colbourn, and Martin Tompa; University of Vermont
Title: Construction of Optimal Quality Control for Oligo Arrays
Oligo arrays are important experimental tools for the high throughput
measurement of gene expression levels. During production of oligo arrays,
it is important to identify any faulty manufacturing step. We describe a
practical algorithm for the construction of optimal quality control
designs that identify any faulty manufacturing step. The algorithm uses
hillclimbing, a search technique from combinatorial optimization. We also
present the results of using this algorithm on all practical quality
control design sizes.
Peng-An Chen and F. K. Hwang, Department of Applied mathematics,
National Chiao-Tung University, Hsinchu, Taiwan 30050 R.O.C.
Title: On a Conjecture of Erdos-Frankl-Furedi on Nonadaptive Group Testing
d-disjunct matrices become the dominating tool in studying nonadaptive
group testing, which has attracted a lot of attention due to its
recent application to pooling designs in DNA mapping. By testing the
items one by one, clearly we can identify n items in n tests. Huang
and Hwang(1999) raised the fundamental question what is the maximum n
such that a d-disjunct matrix has at least n rows? Namely, let N(d)
denote this maximum n for given d. Then for all n £ N(d) the
individual testing algorithm is the best. Erdos, Frankl and
Furedi(1985) studied the same problem in their study of extremal
set theory. They conjuctured that N(d) ³ (d+1)2 and claimed they can
prove for d = 1,2,3. Huang and Hwang(1999) provided the proof for
d = 1,2,3 and also claimed that their method also works for d = 4, but
it would be too messy to produce the details.
We propose a new approach to attack the Erdos, Frankl and Furedi
conjecture. Instead of working diligently on many subclass, and then
piece them together to produce the proof for one d-value, we study the
properties of the d-disjunct matrix at some critical point, namely,
when t = d(d+2) and the d-disjunct matrix is minimal under some
reduction operations. These properties provide a powerful d = 4 case
follows immediately, and d = 5 case can be proved elegantly.
Anthony J. Macula, SUNY Geneseo
Let [t] represent a finite population with t elements. Suppose we
have an unknown d-family of k-subsets C of [t]. We refer to C as the
set of positive k-complexes. In the group testing for complexes
problem, C must be identified by performing 0, 1 tests on subsets or
pools of [t]. A pool is said to be positive if it completely contains
a complex; otherwise the pool is said to be negative. In classical
group testing, each member of C is a singleton. In this talk we
discuss adaptive and nonadaptive algorithms that identify the positive
complexes. We also discuss the problem in the presence of testing
errors. Group testing for complexes has been applied to DNA physical
mapping and has potential application to data mining.
Fred Roberts, Rutgers University - Piscataway, NJ, USA
Title: Consensus List Colorings of Graphs and Physical Mapping of DNA
Abstract: In graph coloring, one assigns a color to each vertex of a graph
so that neighboring vertices get different colors. We shall talk about a
consensus problem relating to graph coloring and discuss the
applicability of the ideas to the DNA physical mapping problem. In
many applications of graph coloring, one gathers data about the
acceptable colors at each vertex. A list coloring is a graph
coloring so that the color assigned to each vertex belongs to the list
of acceptable colors associated with that vertex. We consider the
situation where a list coloring cannot be found. If the data
contained in the lists associated with each vertex are made available
to individuals associated with the vertices, it is possible that the
individuals can modify their lists through trades or exchanges until
the group of individuals reaches a set of lists for which a list
coloring exists. We describe several models under which such a
consensus set of lists might be attained. In the physical mapping
application, the lists consist of the sets of possible copies of a
target DNA molecule from which a given clone was obtained.
Chuan Yi Tang, National Tsing Hua University
Title: Computational Gene Identification by Comparative Genomics Approach
The problem of gene identification is one of the most fascinating problems
in recent bioinformatics research area. Due to the large amount DNA
sequencing data every day in laboratory; scientists are looking for faster
and more accurate computational methods to recognize gene structure. Most
of the existing gene prediction methods only consider a single genome. The
strategies are combined with statistics, special signal sequences (such as
splice sites or promoter), and with homology information in databases.
Here we propose different methods, which apply comparative analysis
between related species. We can identify the important functional regions,
which will tend to be conserved during evolution process between some
human and mouse genomic sequences.
Lusheng Wang, City University of Hong Kong
Title: Approximation Algorithms for Distinguishing Substring Selection Problem
Consider two sets of strings, B (bad genes) and G (good genes), as well
as two integers db and dg (db £ dg). A frequently occurring problem in
computational biology (and other fields) is to find a (distinguishing)
substring s of length L that distinguishes the bad strings from good
strings, i.e., for each string si Î B there exists a length-L substring
ti of si with d(s, ui) £ db (close to bad strings) and for every substring
ui of length L of every string gi Î G, d(s, ui) ³ dg (far from good strings).
We present a polynomial time approximation scheme to settle the problem,
i.e., for any constant e > 0, the algorithm finds a string s of length L
such that for every siÎ B, there is a length-L substring ti of si with
d(t, is) £ (1 + e)db and for every substring ui of length L of every
gi Î G, d(u, is) ³ (1 - e)dg, if a solution to the original pair (db £ dg)
exists. Since there are a polynomial number of such pairs (db, dg), we can
exhaust all the possibililities in polynomial time to find an good
approximation required by the correpsonding application problems.
In any case all these topics are problems in further research.
----------------------------------------------------------------
1according to which the best hypothesis is the one requiring the
smallest number of assumptions.
2or a similarity of the words generated by a scoring system.
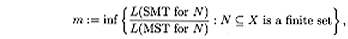 which is called the Steiner ratio. We look for estimates and exact
values for the Steiner ratio in phylogenetic and sequence spaces. In
any metric space the Steiner ratio is at least ½. Phylogenetic
spaces achieves this ratio.
which is called the Steiner ratio. We look for estimates and exact
values for the Steiner ratio in phylogenetic and sequence spaces. In
any metric space the Steiner ratio is at least ½. Phylogenetic
spaces achieves this ratio.
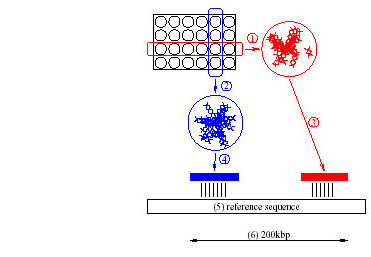 Figure 1: The Pooled Genomic Indexing method maps arrayed clones of
one species onto genomic sequence of another (5). Rows (1) and columns
(2) are pooled and shotgun sequenced. If one row and one column
fragment match the reference sequence (3 and 4 respectively) within a
short distance (6), the two fragments are assigned (deconvoluted) to
the clone at the intersection of the row and the column. The clone is
simultaneously mapped onto the region between the matches, and the
reference sequence is said to index the clone.
3. Experiments We tested the efficiency of the PGI method for
indexing mouse and rat clones by human reference sequences in
simulated experiments. The reference databases included the public
human genome draft sequence, the Human Transcript Database, and the
Unigene database of human transcripts. In one set of experiments we
studied the efficiency of indexing mouse clones with human
sequences. We selected 207 finished clone sequences. Pooling and
shotgun sequencing were then simulated. We compared the performance of
three pooling designs: a simple arrayed design, a random transversal
design with two arrays, and a sparse array design (in which 2-sets of
clones are uniquely identifiable). In contrast to the mouse
experiments, PGI simulation on rat was performed using real shotgun
reads from individual BACs being sequenced as part of the rat genome
sequencing project at HGSC of Baylor College of Medicine. The only
simulated aspect was BAC pooling, for which we pooled reads from
individual BACs computationally. We selected a total of 625 rat BACs
in the rat production database at HGSC. In both sets of experiments,
using relatively few shotgun reads corresponding to 0.5-2.0 coverage
of the clones, 60-90% of the clones can be indexed with human genomic
or transcribed sequences.
References:
[1] Altschul, S. F., T. L. Madden, A. A. Sch¨aer, J. Zhang, Z. Zhang, W. Miller,
and D. J. Lipman 1997. Gapped BLAST and PSI-BLAST: a new generation of protein
database search programs. Nucleic Acids Res., 25:3389?3402.
[2] Cai, W.-W., R. Chen, R. A. Gibbs, and A. Bradley 2001. A clone-array pooled
strategy for sequencing large genomes. Genome Res., 11:1619?1623.
[3] Du, D.-Z. and F. K. Hwang 2000. Combinatorial Group Testing and Its Applications
(2nd ed.). Singapore: World Scientific.
[4] Bruno, W. J., E. Knill, D. J. Balding, D. C. Bruce, N. A. Doggett,
W. W. Sawhill, R. L. Stallings, C. C. Whittaker, and D. C. Torney (1995).
Efficient pooling designs for library screening. Genomics 26, 21?30.
[5] Kautz, W. H. and R. C. Singleton (1964). Nonrandom binary superimposed codes.
IEEE Trans. Inform. Theory, 10:363?377.
[6] D?yachkov, A. G., A. J. Macula, Jr., and V. V. Rykov 2000. New constructions of
superimposed codes. IEEE Trans. Inform. Theory, 46:284?290.
[7] Lander, E. S. and M. S. Waterman 1988. Genomic mapping by fingerprinting random
clones: a mathematical analysis. Genomics, 2:231?239.
Figure 1: The Pooled Genomic Indexing method maps arrayed clones of
one species onto genomic sequence of another (5). Rows (1) and columns
(2) are pooled and shotgun sequenced. If one row and one column
fragment match the reference sequence (3 and 4 respectively) within a
short distance (6), the two fragments are assigned (deconvoluted) to
the clone at the intersection of the row and the column. The clone is
simultaneously mapped onto the region between the matches, and the
reference sequence is said to index the clone.
3. Experiments We tested the efficiency of the PGI method for
indexing mouse and rat clones by human reference sequences in
simulated experiments. The reference databases included the public
human genome draft sequence, the Human Transcript Database, and the
Unigene database of human transcripts. In one set of experiments we
studied the efficiency of indexing mouse clones with human
sequences. We selected 207 finished clone sequences. Pooling and
shotgun sequencing were then simulated. We compared the performance of
three pooling designs: a simple arrayed design, a random transversal
design with two arrays, and a sparse array design (in which 2-sets of
clones are uniquely identifiable). In contrast to the mouse
experiments, PGI simulation on rat was performed using real shotgun
reads from individual BACs being sequenced as part of the rat genome
sequencing project at HGSC of Baylor College of Medicine. The only
simulated aspect was BAC pooling, for which we pooled reads from
individual BACs computationally. We selected a total of 625 rat BACs
in the rat production database at HGSC. In both sets of experiments,
using relatively few shotgun reads corresponding to 0.5-2.0 coverage
of the clones, 60-90% of the clones can be indexed with human genomic
or transcribed sequences.
References:
[1] Altschul, S. F., T. L. Madden, A. A. Sch¨aer, J. Zhang, Z. Zhang, W. Miller,
and D. J. Lipman 1997. Gapped BLAST and PSI-BLAST: a new generation of protein
database search programs. Nucleic Acids Res., 25:3389?3402.
[2] Cai, W.-W., R. Chen, R. A. Gibbs, and A. Bradley 2001. A clone-array pooled
strategy for sequencing large genomes. Genome Res., 11:1619?1623.
[3] Du, D.-Z. and F. K. Hwang 2000. Combinatorial Group Testing and Its Applications
(2nd ed.). Singapore: World Scientific.
[4] Bruno, W. J., E. Knill, D. J. Balding, D. C. Bruce, N. A. Doggett,
W. W. Sawhill, R. L. Stallings, C. C. Whittaker, and D. C. Torney (1995).
Efficient pooling designs for library screening. Genomics 26, 21?30.
[5] Kautz, W. H. and R. C. Singleton (1964). Nonrandom binary superimposed codes.
IEEE Trans. Inform. Theory, 10:363?377.
[6] D?yachkov, A. G., A. J. Macula, Jr., and V. V. Rykov 2000. New constructions of
superimposed codes. IEEE Trans. Inform. Theory, 46:284?290.
[7] Lander, E. S. and M. S. Waterman 1988. Genomic mapping by fingerprinting random
clones: a mathematical analysis. Genomics, 2:231?239.
