Edgar Garduno, University of California, San Diego
Boundary Tracking for Both the Simple Cubic and the Face-Centered
Cubic Grids
Biomedical imaging is an example of an area greatly benefited
from mathematics, computer science and engineering. In a
typical three-dimensional (3D) medical imaging application a
series of steps have to be taken: acquisition, post-processing,
and display. Modern medical imaging devices generate sets of
numbers, or images, representing a given region of the body.
In general, these sets of numbers are discrete representations
of real objects obtained by either direct sampling the objects
or by using a reconstruction algorithm. The final set of numbers
is arranged in a 3D grid, we refer to the set of points to which
the samples of an object are located as a grid. Every point in
the grid is associated to a volume element or voxel; moreover,
a voxel can be referred to by the grid point with which it is
associated. A common practice is to assign a real value to each
voxel, i.e., gray value, such that the given value is proportional
to some physical property of the body imaged. A common grid used
in biomedical imaging is the simple cubic grid, whose associated
voxels are cubic voxels, because is the easiest to implement in
current computers.
The discrete approximation of the object has to be further processed
after acquisition (e.g., filtered and segmented). One reason for
post-processing the discrete object is that the image is corrupted
by noise and artifacts introduced by either the physics of the
imaging device, the acquisition techniques, the limitations of the device or
the inaccuracies of reconstruction algorithms. Another reason
for post-processing is the wish, or need, to observe only a section
of the object imaged, e.g., the desire to observe an organ. In order
to carry out the post-processing operations is also important to
consider the arrangement of the voxels in space, the way voxels
are adjacent to each other and the different way gray values are
assigned to voxels. For example, in the simple cubic grid, voxels
can be considered to be adjacent in several ways: face, face-or-edge
or face-or-edge-or-vertex. The final result of the post-processing
operations is a subset of voxels, or segmented image, that
conjecturally approximate more precisely the object to be analyzed.
Finally, the resulting subset of voxels is typically further
processed to make it appropriate for displaying on a computer
screen. One of the typical techniques to create final displays
is surface rendering. In this technique we assume that the subset
of voxels is an accurate approximation of the volume of the object
to be analyzed and that the interior of the object is of no
interest. Consequently, the surface enclosing the volume is
enough to represent the object on a computer screen. In the case
of cubic grids, the surface is a collection of square faces that
define the boundary between the interior of the object and its
exterior (the final representation on the computer screen is
created using standard computer graphics techniques). Several
techniques have developed to obtain the collection of square
faces that represent the surface of a subset of cubic voxels,
also known as boundary tracking algorithms. Notably, to obtain
such collection is also essential to consider the properties
of the arrangement of the grid points, the relation between
its associated voxels and the gray values assigned to the
voxels.
The increasing use of digital computers to carry out the
processing of information has led to the development of a
mathematical theory to deal with the information represented
in a discrete fashion, i.e., geometry of digital spaces. The
geometry of digital spaces is a theory capable of dealing with
various grids (or tesellations of space), adjacencies between
grid points, different assignments of values to voxels and
operations performed with them. An important result of the
use of the theory of digital spaces is that there are other
grids that are more convenient to discretize an object and
to carry out image processing. One of such grids is the
face-centered cubic grid, i.e., fcc grid. The voxels
associated with the points in the fcc grid are rhombic
dodecahedra (polyhedra with 12 identical rhombic faces).
Significantly, the fcc grid is a subset of the simple cubic
grid, a fact that allows to take advantage of some existing
algorithms for the simple cubic grid. We present a boundary
tracking algorithm capable of producing boundaries for 3D
binary images modeled either with cubic voxels or rhombic
dodecahedral voxels.
Furthermore, boundaries utilizing cubic voxels have some
undesirable properties. One of them is that the 90-degree
angle between the faces of a cubic voxel results in a
"blocky" appearance when displayed on a computer screen.
We diminish this problem by using rhombic dodecahedral voxels.
Leo Joskowicz, School of Computer Science and Engineering, The
Hebrew University of Jerusalem, Israel
Computer-Aided Navigation and Positioning in Orthopaedic Surgery
The past ten years have witnessed the development and deployment of a
variety of computer-aided system for orthopaedic surgery. The goals of
these systems are to enhance the surgeon's dexterity, visual feedback, and
information integration before and during surgery. Computer-aided
orthopaedic surgery (CAOS) systems aim at improving the accuracy and
steadiness of the surgical gestures, reduce complications due to tool and
implant misplacement, reduce cumulative exposure to X-ray radiation, and
reduce surgery time and patient morbidity. CAOS surgeries, such joint,
trauma and ligament surgeries, are beginning to have an impact on routine
clinical practice.
In this talk, we survey the clinical results and technical state of the art
in computer-aided orthopaedic surgery (CAOS). After a brief overview of the
most common orthopaedic surgeries, we identify their common characteristics
and the desirable system goals in terms of accuracy, resolution,
robustness, repeatability, and computation and reaction time. We then
describe the technical characteristics of existing imaging (X-ray,
ultrasound, CT, and MRI), tracking (optical, electromagnetic, and
gyroscopic), and robotic systems. We classify navigation systems into four
categories: 1. CT-based; 2. Fluoroscopic X-ray based; 3. CT+Fluoroscopic
X-ray based; and 4. CT-less spatial navigation, and robotic systems into
two categories: 1. positioning and guiding aids, and; 2. active execution
systems. For each, we describe the state of the art, its current clinical
applications, and its pros and cons. We identify key technical challenges
and propose possible solutions. We conclude with perspectives for the
emerging field of medical CAD/CAM and its expected impact on orthopaedic
surgery.
D. B. Karron, Computer Aided Surgery, Inc.
Early experience using Digital Morse Theory for Medical Image Segmentation at
Computer Aided Surgery, Inc.
Extracting precise and accurate objective measurements from image data has been an
enduring problem in biomedical engineering. We are in the midst of an explosion of
mega pixels from imaging technology. Imaging, from reflected, structured, and
transmitted visible light, infrared, ionizing radiation, ultrasound, planar images,
tomography, and the admixture of these, has vast application for in image guidance in
many applications from image guided surgery to surgical simulation and education. The
explosion of pixels from these technologies has motivated our efforts to understand these
images in terms of well-defined objects. Further we wish to understand the
interrelationship amongst these objects. We are meeting this challenge by the
development by the extension of basic mathematical theory from Morse Theory into the
pixilated digital domain wit Digital Morse Theory.
Digital Morse Theory is an extension of traditional Morse Theory developed by Marsdon
Morse in the 1930's and 1940's at the Princeton Institute for Advanced Studies. The
essential idea of Morse Theory is to describe the topology of a function as opposed to the
geometry of a function in terms of Morse Criticalities. Traditionally, Morse theory
required an analytic description of a function that was twice differentiable and
continuous. Digital Morse Theory, as being developed by Cox and Karron with recent
work by Jack Snoyink et al, attempts to adapt Morse’s concept of criticalities to discrete
image data measurements. This has many practical applications in multidimensional
image segmentation in that we can describe all of the objectively segmentable objects in
terms of their parent, progeny, and peer criticalities in what we are terming a Morsian
organization. A Reeb graph describes the relationship of objects to one another; we are
programming a demonstration of the application of Digital Morse Theory for medical
image segmentation that shows a catalog of all of the segmentable objects and permits
the user to organize component objects into desired ensembles of anatomic objects
quickly, precisely, and accurately.
Sample medical images from the CT and MRI images of the Visible Human Project and
their associated DMT graph will be presented. We will demonstrate the relationship
between the DMT graph and image components and how we can build a 3d scene of
segmented objects with important projects for anatomic surgical modeling. Specifically,
we desire anatomic dimensional fidelity and accuracy, as we will use these models to
make critical care decision. Since models derived from DMT based segmentation have
the Jordan and Manifold surfaces, this means that disparate segmented objects do not
have interpenetrating surfaces or other geometric pathologies.
Our goal is to have semi-automatic to fully automatic segmentation and fusion of
disparate medical images.
A. Kuba, Dept. of Applied Informatics, University of Szeged, Hungary
Discrete Tomography from Absorbed Projections
Consider a set of points in the space where all of the points emit the
same intensity of radioactivity. Suppose that the space is filled with
some homogeneous material having known absorption coefficient. There are
detectors measuring the so-called absorbed projections, that is, the sums
of the partially absorbed activities along lines between the point sources
and the detectors. The problem is to reconstruct the point set from its
absorbed projections. This model is similar to the acquisition technique
used, for example, in the nuclear medicine, where the radioactivity
emitted from the administered radiopharmacon is partially absorbed in the
human body before detection.
This new direction of discrete tomography has a few interesting uniqueness
results and reconstruction algorithms in special cases. For example, the
reconstruction of discrete sets from two absorbed projections is studied
if the absorption coefficient is log((1+sqrt(5))/2). A necessary and
sufficient condition is given for the uniqueness and a reconstruction
algorithm is suggested in this special case. It is proved that the
reconstruction of so-called hv-convex discrete sets from such projections
can be done in polynomial time. In this presentation we are going to
generalize these results for different absorption values and for more than
two projections.
Eva K. Lee1,2,3, Tim Fox2 and Ian Crocker2
Beam Geometry and Intensity Map Optimization in
Intensity- Modulated Radiation Therapy via Combinatorial
Optimization
In this talk, we describe the use of mixed integer programming for
simultaneously determining optimal beamlet fluence weights and beam
angles in intensity-modulated-radiation-therapy treat-ment
planning. In particular, binary variables are used to capture
use/non-use of each beam, and continuous variables capture intensity
values for each beamlet. For the tumor, explicit constraints include
coverage with tumor underdose specified, conformity, and homogeneity;
while DVH re-strictions for critical structures and normal tissues are
imposed. Our algorithmic design thus fax has been motivated by
clinical cases. To set up the model, 16-24 coplanar candidate fields
of size 20x2O cm2 are generated, each consisting of 1600
5mm-beamlets. The maximum number of fields in the final plan will be
constrained. Numerical tests are performed and analyzed on three tumor
sites: 1)head-and-neck tonsil, 2)posterior-fossa-boost, and
3)prostate. In all cases, homogeneity is kept below 1.25, while
requiring 95% tumor-volume coverage by the 100% isodose-curve and 100%
tumor-coverage by the 95% isodose-curve. Optimal plans are obtained
when maximum number of fields are restricted from 6-24
fields. Sensitivity of quality of plans versus various objective
functions are compared and analyzed. For a practical 8-field practical
plan, optimal results in the quality of plans for the head-and-neck
tonsil case and the posterior fossa boost occur when the conformity is
minimized in the objective function. In the prostate cancer case,
there are overlapping boundary points in the rectal wall and the
prostate, and the best quality plan (for 8-fields) results from an
objective which minimizes the total weighted dose to the rectum and
bladder, together with a tight ring of 5mm-thick normal tissue drawn
around the prostate-PTV. The deviation in best objective choice use
may result from the closeness of the rectal wall (and the bladder) to
the prostate with overlapping boundary points.
1 School of Industrial and Systems Engineering, Georgia Institute of Technology, Atlanta, Georgia.
2Department of Radiation Oncology, Emory University School of Medicine, Atlanta, Georgia.
3Corresponding author, evakylee@isye.gatech.edu
Ming C. Lin, Department of Computer Science, University of North Carolina at Chapel Hill
Geometric Algorithms for Modeling Deformable Bodies
Modeling deformation is a key component for many technology
assisted medical procedures, such as image-guided surgery,
multi-modal image registration, surgical planning and training,
instructional medical illustration. In this talk, we discuss
geometric issues involved in simulating interaction between
flexible bodies and present efficient algorithms for a subset
of these problems.
Some of the challenging research issues include rapid detection
of contacts, efficient enforcement of non-penetration constraints,
and fast contact resolution. We describe two classes of geometric
algorithms for computing "deformed distance fields" dynamically
using fast-marching level-set methods and modern graphics hardware.
We introduce the concept of "multi-level simulation acceleration"
techniques for enhancing the performance of simulators used in
modeling deformation. We demonstrate the effectiveness of our
approaches on moderately complex animated scenes and medical
simulations.
Danny Z. Chen, Xiaobo S. Hu, Shuang Luan and Chao Wang,
Department of Computer Science and Engineering,
University of Notre Dame
Charles E. Lee, Shahid A. Naqvi and Cedric X. Yu, Department of Radiation Oncology
University of Maryland Medical School
Xiaodong Wu, Department of Computer Science,
The University of Texas - Pan American
Geometric Algorithms and Experiments for Static Leaf Sequencing
Problems in Radiation Therapy
Radiation therapy uses radiation beams to eradicate tumors while
sparing surrounding vital organs and healthy tissues. A good shape
matching between the tumor volume and radiation beams is critical to
the quality of treatments. In general, tumors have vaxious sizes and
shapes, while the radiation beams generated by the linear accelerators
(LINAC) (machines that are used to generate and deliver radiation) are
cylindrical. One way to overcome the poor shape matching problem with
LINAC is to use a device called multileaf collimator (MLC), which uses
a set of opposing tungsten leaves to vary the cylindrical beam shape
in order to obtain the needed discrete dose distributions. However,
one of the challenging issues of using a collimator is its potentially
prolonged treatment time. The static leaf sequencing (SLS) problem
axises in radiation therapy for cancer treatments, aiming to
accomplish the delivery of a radiation prescription to a taxget tumor
using an MLC in the minimum amount of delivery time.
Geometrically, the SLS problem can be formulated as a 3-dimensional
partition problem for which the 2-dimensional problem of partitioning
a polygonal domain (possibly with holes) into a minimum set of
monotone polygons is a special case. In this talk, we present new
geometric algorithms for a basic case of the 3-D SLS problem (which is
also of clinical value) and for the general 3-D SLS problem. Our basic
3-D SLS algorithm, based on new geometric observations, produces
guaxanteed optimal quality solutions using Steiner points in
polynomial time; the previously best known basic 3-D SLS algorithm
gives optimal outputs only for the case without using Steiner points,
and its time bound involves a multiplicative factor of a factorial
function of the input. Our general 3-D SLS algorithm is based on our
basic 3-D SLS algorithm and a polynomial time algorithm for
partitioning a polygonal domain (possibly with holes) into a minimum
set of x-monotone polygons, and has a fast running time.
Experiments and compaxisons using real medical data and on a real
radiotherapy machine have shown that our 3-D SLS algorithms and
software produce treatment plans that use significantly shorter
delivery time and give better treatment quality than the current most
popular commercial treatment planning system and the most well-known
SLS algorithm. Some of our techniques and geometric procedures (e.g.,
for the problem of partitioning a polygonal domain into a minimum set
of x-monotone polygons) axe interesting in their own right.
Dimitris Metaxas, Rutgers University
Segmentation, Modeling and Estimation Techniques for Internal Organs
3D segmentation and modeling for improved medical diagnosis of disease
promises to revolutionize the way medical practice is done currently
which is inherently 2D. In this talk we will first present our 3D
hybrid segmentation framework which consists of integrating low level
image processing and higher level deformable models. We will show
semgentations of a variety of organs including brains, the heart and
the colon. In the second part we will present our 3D stress-strain
estimation framework of the heart's shape, motion and material
properties from MRI-SPAMM.
Neil Molino, Stanford University
Deformable Bodies: Mesh Generation and Simulation
The generation of meshes for deformable bodies and the subsequent
simulation of their motion are used in a number of areas including
fracture, haptics, solid modeling, surgical simulations, and the
modeling of biological tissue including the brain, the knee and even
fatty tissue. Robust methods for generating these meshes are in high
demand. Of particular interest to us are simulations of highly
deformable bodies such as cloth (skin) and the muscle and fatty
tissues commonly encountered in graphics, biomechanics, or virtual
surgery. We propose a new mesh generation paradigm that gives
particular consideration to conditioning the mesh for high
deformation. We further discuss innovations for the simulation of
deformable objects including a finite volume method for volumetric
simulation, collision resolution, and internal dynamics modeling for
cloth.
Our new mesh generation algorithm produces both high quality elements
and a mesh that is well conditioned for subsequent large
deformations. We primarily focus on tetrahedral meshes, but use this
algorithm for surface meshing as well. We use a signed distance
function defined on a grid in order to represent the object
geometry. In the volumetric case, after tiling space with a uniform
lattice based on crystallography, we identify a subset of these
tetrahedra that adequately fill the space occupied by the object. Then
we use the signed distance function or other user defined criteria to
guide a red green mesh subdivision algorithm that results in a
candidate mesh with the appropriate levels of detail. After this, both
the signed distance function and topological considerations are used
to prune the mesh as close to the desired shape as possible while
keeping the mesh flexible for large deformations. Finally, we compress
the mesh to tightly fit the object boundary using either masses and
springs, the finite element method, or an optimization approach to
relax the positions of both the interior and boundary nodes. The
resulting mesh is well-suited for simulation since it is highly
structured, has robust connectivity in the face of deformation, and is
readily refined if deemed necessary during a subsequent simulation.
Mesh generation is not only a broad field, but is in some sense many
fields each concerned with the creation of meshes that conform to
quality measures specific to the application at hand. The requirements
for fluid flow and heat transfer, where the mesh is not deformed, and
for small deformation solids where the mesh is barely deformed, can be
quite different from those for simulating soft biological tissue that
may undergo large deformations. For example, while an optimal mesh for
a fluid flow simulation should include anisotropically compressed
elements in boundary layers, these highly stretched cells tend to be
ill-conditioned when a mesh deforms significantly as is typical for
soft bodies. Either the mesh is softer in the thin direction and the
cell has a tendency to invert, or the mesh is stiffer in the thin
direction and the simulation becomes very costly as the time step
shrinks with higher stiffness and smaller element cross-section. Thus,
although our method has been designed to provide a high degree of
adaptivity both to resolve the geometry and to guarantee quality
simulation results, we neither consider nor desire anisotropically
stretched elements. Also, since highly deformable bodies tend to be
devoid of sharp features such as edges and corners, we do not consider
boundary feature preservation here. However, we believe that our
algorithm can be extended to treat this case and plan to pursue it as
future work.
Our main concern is to generate a mesh that will be robust when
subsequently subject to large deformations. For example, although we
obviously want an adaptive mesh with smaller elements in areas where
more detail is desired, it is even more important to have a mesh that
can be adapted during the simulation since these regions will
change. Motivated by crystallography, we use a body-centered cubic
(BCC) mesh that is highly structured and produces similar (in the
precise geometric sense) tetrahedra under regular refinement. This
allows us to adaptively refine both while generating the mesh and
during the subsequent simulation.
Beginning with a uniform tiling of space, we then use a signed
distance function representation of the geometry to guide the creation
of the adaptive mesh, the deletion of elements that are not needed to
represent the object of interest, and the compression of the mesh
necessary to match the object boundaries. This compression stage can
be carried out using either a mass spring system, a finite element
method, or an optimization based approach. One advantage of using a
physically based compression algorithm is that it gives some
indication of how a mesh is likely to respond to the deformations it
will experience during simulation. This is in contrast to many
traditional methods that may produce an initial mesh with good quality
measures, but also with hidden deficiencies that can be revealed
during simulation leading to poor accuracy or element collapse.
In addition to testing the mesh with the physics based compression
algorithm, we identify and guarantee several topological properties
that ensure the mesh is sufficient for high deformation, for example a
tetrahedron with all four of its edges on the boundary or an internal
edge with both nodes on the boundary can limit the accuracy of the
simulation, or worse, allow collapse.
We have generated tetrahedral meshes with this algorithm and used them
in the simulation of highly deformable objects with a variety of
constitutive models using several simulation techniques. The meshes
retained their quality throughout all of these simulations. One new
simulation technique that we tried is the finite volume method (FVM),
which is more intuitive than the finite element method (FEM), since it
relies on a geometrical rather than variational framework. We show
that FVM allows one to interpret the stress inside a tetrahedron as a
simple ``multidimensional force'' pushing on each face. Moreover, this
interpretation leads to a heuristic method for calculating the force
on each node, which is as simple to implement and comprehend as masses
and springs. In the finite volume spirit, we also present a geometric
rather than interpolating function definition of strain. We illustrate
that FVM places no restrictions on the simulation of volumetric
objects subject to large deformations, in particular using a
quasi-incompressible, transversely isotropic, hyperelastic
constitutive model for simulating contracting muscle tissue. B-spline
solids are used to model fiber directions, and the muscle activation
levels are derived from key frame animations.
Significant effort has been placed into accelerating FEM calculations
including recent approaches that precompute and cache various
quantities, modal analysis, and approximations to local rotations. In
spite of significant effort into alternative (and related) methods for
the robust simulation of deformable bodies, FVM has been largely
ignored. Two aspects of FVM make it extremely attractive. First, it
has a firm basis in geometry as opposed to the FEM variational
setting. This not only increases the level of intuition and the
simplicity of implementation, but also increases the likelihood that
aggressive but robust optimizations might be found. Second, there is a
large community of researchers using these methods to model solid
materials subject to very high deformations. For example, it has been
used with subcell pressures to eliminate the artificial hour-glass
type motions that can arise in materials with strongly diagonally
dominant stress tensors, such as incompressible biological materials.
We are particularly interested in the simulation of both active and
passive muscle tissue. Biological tissues typically undergo rather
large nonlinear deformations, and thus they create a stringent test
for any simulation method. Moreover, they tend to have complex
material models with quasi-incompressibility, transverse anisotropy,
hyperelasticity, and both active and passive components. In this
paper, we use a state of the art constitutive model, B-spline solids
to represent fiber directions, and derive muscle activations from key
frame animation.
The general theme of our mesh generation algorithm---tile ambient
space as regularly as possible, select a subset of elements that are
nicely connected and roughly conform to the object, then deform them
to match the boundary---is applicable in any dimension and on general
manifolds. We have used this idea to triangulate two-dimensional
manifolds with boundary. We begin with a complete quality mesh of the
object (actually created as the boundary of a tetrahedral mesh from
our method, with additional edge-swapping and smoothing), and a level
set indicating areas of the surface to trim. We keep a subset of the
surface triangles inside the trimming level set and compress to the
trimming boundary, making sure to stay on the surface. This can also
be done for parametric surfaces with a triangulation in parameter
space and a trimming level set defined either in three-dimensional
space or in the parameter space. Quality two-dimensional surface
meshes with boundary are especially important for cloth
simulation. We, therefore, used cloth modeling as a testbed for our
surface meshes. Two of the significant concerns in cloth simulation
are collision resolution and internal dynamics modeling. A quality
mesh free of slivers is important for well-conditioned numerical
algorithms for both of these issues, particularly internal
dynamics.
Collisions are a major bottleneck in cloth simulation. Since all
points are on the surface, all points (and there will be many
thousands for reasonably resolved simulations) may potentially collide
with each other and the environment in any given time step. We argue
that it is essential to maintain the constraint that the cloth mesh
can never intersect itself. This can be efficiently achieved by a
novel combination of fast and numerically well-conditioned penalty
forces with a fail-safe geometric method. For dealing with collisions
with large volumetric objects in the environment we demonstrate a
technique for pushing the cloth to the surface of the objects while
still preserving wrinkles and other features. Motivated by Newmark
central schemes we demonstrate a time integration algorithm that
decouples the collision dynamics from the interior cloth dynamics.
Cloth internal dynamics can be broken up into in-plane deformations
(stretching and shearing) and bending. Bending is visually the most
fundamental characteristic of cloth, yet it is not well
understood. Working from basic principles we derive the only
reasonable family of bending spring models that operate on triangle
meshes, and show results with the simplest and most efficient member
of this family. Our model easily permits non-flat rest poses, which
allow the simulation of non-flat manifolds (e.g. skin) as well as
pre-sculpted wrinkles and folds in cloth to maintain the desired
artistic look of a garment during motion.
When simulating highly deformable objects, using a mesh designed for
that purpose is obviously very important. Our new meshing algorithm
produces such a mesh and has been tested in various simulations. As
future work, we plan to explore the interplay between the mesh
generation phase and the simulation phase for deformable bodes, for
example allowing the mesh to slip during the simulation.
Dinesh K. Pai, Rutgers University
Geometric Problems in Ultrasound Imaging
Ultrasound imaging is widely used in medicine because it is safe and
interactive. However, raw ultrasound images have significant noise
and artifacts relative to other imaging techniques such as CT and MRI,
and present interesting algorithmic challenges for extracting useful
geometric information. In this talk I will describe the fundamentals
of ultrasound imaging, and some of our recent work in extracting 3D
geometry from free-hand ultrasound images and for improving ultrasound
image quality. (Joint work with Rohling, Salcudean, Wei, and Zhang).
P. M. Pardalos1, J. C. Sackellares2, D. S. Shiau2, and V. A.
Yatsenko2
- (1) Center for Applied Optimization and ISE Department University of
Florida, Gainesville, FL
- (2) Departments of Neurology and Neuroscience, University of Florida,
Gainesville, FL
Computational Geometry and Spatiotemporal Dynamics of the Epileptic Human Brain: Optimization, Control and Prediction
The existence of complex chaotic, unstable, noisy and nonlinear
dynamics in brain electrical activity requires new approaches to the
study of brain dynamics. One approach is the combination of combining
certain geometric concepts, control approach, and optimization. In
this paper we discuss the use of a differential geometric approach to
the control of Lyapunov exponents and the characterization of
statistical information to predict and ``correct'' brain
dynamics. This approach assumes that information about the
physiological state (in this case the electrocencephalogram) comes in
the form of a nonlinear time series with noise. The approach involves
a geometric description of Lyapunov exponents for the purpose of
correcting of the nonlinear process that provides adaptive dynamic
control. We separate the Lyapunov exponents into tangent space (fiber
bundle) and its functional space. Control involves signal processing,
calculation of an information characteristic, measurement of Lyapunov
exponents, and feed-back to the system. With more information, we can
reduce uncertainty by a certain degree. We demonstrate the
computational aspects of the proposed geometric approach on the base
of different mathematical models in the presence of noise of various
origins. We review the EEG signal, and outline a typical application
of the geometrical representation: three dimensional reconstruction of
Lyapunov exponents and correlation dimension obtained from EEG
data. The novelty in this paper is in the representation of dynamical
and information characteristics in three dimensional vector space in a
way that permits practical applications. We discuss an application of
this approach to the development novel devices for seizure control
though electromagnetic feed-back.
Achim Schweikard, Informatik, Universtat Luebeck, Germany
Planning and Navigation for Robotic Radiosurgery
Stereotactic radiosurgery uses focused beams of radiation from
multiple spatial directions to ablate brain tumors. To plan the
treatment, spatial directions of the beams must be determined in a
first step. The set of such beam directions should be chosen such that
the dose to surrounding healthy tissue remains minimal, and the tumor
absorbs a homogeneous dose throughout its volume. In addition to
choosing the beam directions, one must find the weight for each such
beam direction, i.e. the activation duration for the beam.
Earlier systems for stereotactic radiosurgery are inherently limited
to treat lesions in the brain. The first goal of robotic radiosurgery
is to improve conventional stereotactic radiosurgery with respect to
accuracy. A second, more important goal is to allow for treating
lesions anywhere in the body.
In the first part of this talk, we present planning methods for
robotic radiosurgery. Our methods are based on linear
programming. Linear programming gives a fast and globally convergent
optimisation strategy. It has been proposed as a planning technique in
radiation therapy applications by several authors. In robotic
radiosurgery, up to 1500 beam directions are used for a single
treatment, and the beam can be moved in space with full kinematic
flexibility. We show that the general approach of linear programming
is practical for robotic radiosurgery, where a very large number of
beam directions is used. An implementation of our methods has been
incorporated into the Cyberknife robotic radiosurgery system. Several
thousand patients with tumors of the brain, the spine and the lung
have been treated with the described linear programming based planning
system.
The second part of this talk addresses the problem of navigation for
robotic radiosurgery. Conventional stereotactic radiosurgery is
limited to the brain. Tumors in the chest and the abdomen move during
respiration. The ability of conventional radiation therapy systems to
compensate for respiratory motion by moving the radiation source is
inherently limited. Since safety margins currently used in radiation
therapy increase the radiation dose by a very large amount, an
accurate tracking method for following the motion of the tumor is of
utmost clinical relevance. We investigate methods to compensate for
respiratory motion using robotic radiosurgery. Thus, the therapeutic
beam is moved by a robotic arm, and follows the moving target
tumor. To determine the precise position of the moving target we
combine infrared tracking with synchronized X-ray imaging. Infrared
emitters are used to record the motion of the patient's skin
surface. A stereo X-ray imaging system provides information about the
location of internal markers. During an initialisation phase (prior to
treatment), the correlation between the motions observed by the two
sensors (X-ray imaging and infrared tracking) is computed. This model
is also continuously updated during treatment to compensate for other,
non-respiratory motion. Experiments and clinical trials suggest that
robot-based methods can substantially reduce the safety margins
currently needed in radiation therapy. Our correlation based
navigation method has since been incorporated into the Cyberknife
robotic radiosurgery system. Our new module is in routine clinical use
at a growing number of sites worldwide.
References:
- Schweikard, A., Glosser, G., Bodduluri, M., Adler, J. R., Robotic Motion Compensation for
Respiratory Motion during Radiosurgery Journal of Computer-Aided Surgery, vol. 5, no
4., 263-277, Sept. 2000.
- Schweikard, A., Bodduluri, M., Adler, J. R.: Planning for Camera-Guided Radiosurgery, IEEE
Transactions on Robotics and Automation, 13, 6, 951-962, 1998.
Marcelo Siqueira1, Tessa Sundaram2, Suneeta Ramaswami3,
Jean Gallier1, James Gee4
Quadrilateral Meshes for the Registration of Human Brain Images
- (1) Department of Computer and Information Science, University of Pennsylvania
- (2) School of Medicine and Department of Bioengineering, University of Pennsylvania
- (3) Department of Computer Science, Rutgers University
- (4) Department of Radiology, University of Pennsylvania
Frederic F. Leymarie and Benjamin B. Kimia, Brown University
Shock Scaffolds for 3D Shapes in Medical Applications
Demetri Terzopoulos, Courant Institute, New York University
Deformable Models for Medical Image Analysis
The modeling of biological structures and the model-based
interpretation of medical images present many challenging problems. I
will describe a powerful modeling paradigm, known as deformable
models, which combines computational geometry, computational physics,
and estimation theory. Deformable models evolve in response to
simulated forces as dictated by the continuum mechanical principles of
flexible materials expressed via variational principles and PDEs. The
talk will review several biomedical applications currently under
development, including image segmentation using dynamic finite element
and topologically adaptive deformable models, as well as our recent
work on ``deformable organisms''. The latter aims to automate the
segmentation process by augmenting deformable models with behavioral
and cognitive control mechanisms from our work on artificial life.
Jayaram K. Udupa, University of Pennsylvania
Fuzzy Connectedness and Image Segmentation
Image segmentation - the process of defining objects in images - remains
the most challenging problem in image processing despite decades of
research. Many general methodologies have been proposed to date to
tackle this problem. An emerging framework that has shown considerable
promise recently is that of fuzzy connectedness. Images are by nature
fuzzy. Object regions manifest themselves in images with a heterogeneity
of image intensities owing to the inherent object material
heterogeneity, and artifacts such as blurring, noise and background
variation introduced by the imaging device. In spite of this gradation
of intensities, knowledgeable observers can perceive object regions as a
gestalt. The fuzzy connectedness framework aims at capturing this notion
via a fuzzy topological notion called fuzzy connectedness which defines
how the image elements hang together spatially in spite of their
gradation of intensities. In defining objects in a given image, the
strength of connectedness between every pair of image elements is
considered, which in turn is determined by considering all possible
connecting paths between the pair. In spite of a high combinatorial
complexity, theoretical advances in fuzzy connectedness have made it
possible to delineate objects via dynamic programming at close to
interactive speeds on modern PCs. This paper gives a tutorial review of
the fuzzy connectedness framework delineating the various advances that
have been made. These are illustrated with several medical applications
in the areas of Multiple Sclerosis of the brain, MR and CT angiography,
brain tumor, mammography, upper airway disorders in children, and
colonography.
A. Frank van der Stappen, Universiteit Utrecht
(joint work with Han-Wen Nienhuys)
Simulating cuts in triangulated objects
The motivation of our work on simulating cuts is formed by
interactive surgery simulations. Such simulations combine
interactive deformation of virtual tissue with simulations of
surgical procedures. The Finite Element Method (FEM) seems suited for
computing deformation since it is physically accurate. Meshes form
the basis of this technique: the domain of the problem is subdivided
in geometric primitives (`elements') such as tetrahedra or triangles.
With this subdivision the governing partial differential equation (PDE)
can be transformed in a system of numerical equations.
For the rest of the discussion, we will assume that the PDE is linear
and derives from an elasticity problem. The equations can then be
discretized into a
linear system, where the matrix is called stiffness matrix.
Finding a solution is a two step process: first, the stiffness matrix
is constructed, then the unknowns (a set of deformations) are computed
from the stiffness matrix and given loads. The characteristics of a
mesh influence both steps. The accuracy of the discretization process
is determined by element shapes. For triangular/tetrahedral meshes, large
elements
and large angles decrease the accuracy of the FEM discretisation.
The accuracy of the solution process in finite precision arithmetic is
determined by the condition number of the stiffness matrix, where a
lower condition number is better. The convergence speed of iterative
solution methods also depends on the condition number. This holds for
both the conjugate gradient algorithm (a static approach), and for
damped dynamic relaxations using explicit time integration. The
condition number of a complete stiffness matrix can be bounded by the
condition numbers for separate elements. In contrast to the FEM
discretisation error, high condition numbers are caused by elements
with small sizes and small angles. So, the requirements for optimal accuracy
in the discretisation and for optimal speed and accuracy in the
numerical process are contradictory. However, it is safe to say that
a mesh with `round' (non-flat) elements and bounded element sizes is a
good general purpose mesh.
Iterative algorithms seem well suited as numerical solution strategies
for surgery simulations, since they allow on-line meshchanges.
If such an iterative approach is used, then mesh quality becomes an
issue of vital importance: the maximum size of simulations is largely
determined by mesh characterics: better meshes yield faster
convergence, enabling larger and more accurate simulations. It follows
that simulated surgical manipulations (such as needle insertions,
cuts, and cauterizations) should be designed to keep mesh quality
high. Secondly, the manipulations should also keep the complexity of
the mesh low, since the cost of a single iteration step is
proportional to the size of the mesh.
We state the general mesh cutting problem as follows: given a starting
mesh, and positions of a user-controlled scalpel, modify the mesh at
every moment to show an incision that represents the past trajectory
of the scalpel, and ends exactly at the scalpel. The challenge is to
do so while maintaining the quality and size of the mesh.
Simulation of cuts in surgery simulation is related to simulation of
other destructive surgical procedures. The first operation to have
been simulated on volumetric meshes is cauterization. This was done
by removing elements in contact with a virtual cauterization
tool. A disadvantage when applied to cutting is that it produces
a jagged surface on the virtual tissue.
For cutting, subdivision methods have been the norm: elements that are
in contact with the scalpel are subdivided to produce a cut conforming
to the scalpel position. Subdivision methods always increase the size
of the mesh. Moreover, these methods tend to produce degeneracies:
mesh modification is done only within a fixed region of the mesh, and
if the scalpel moves close to the boundary of that region, poorly-shaped
elements are inevitable. Research has been done to counter the
the degeneracies---caused by subdivision cutting---by collapsing short
edges of the mesh. This approach does improve the quality of the mesh,
but this solution does not repair all inconsistencies: not all edges may
be contracted, and flat triangles and tetrahedrons, which do not contain
short edges but are still degenerate, are not dealt with.
Our first approach to cutting in tetrahedralized objects keeps the
mesh size at the initial level by performing cuts only along faces
of the mesh, which are selected according to a heuristic. Nodes of the
mesh are relocated to align these faces with the trajectory of the
virtual scalpel. We have implemented this approach and the results
confirm that the mesh size remains small. In addition, the method
also creates only few short edges. There are, however, also some
disadvantages. Since no new nodes are created, the resolution of
the cut is bounded by the mesh resolution, which results in a less
accurate representation of the cut in the unlikely case of sharp turns
in the scalpel path. A more serious problem is that snapping can result
in degenerate elements in the mesh. Such degeneracies are dealt with
by subdividing flat elements, and collapsing the resulting short edges,
effectively removing the flat element. Unfortunately, not all edges
can be collapsed. Using only existing mesh features as a basis for mesh
modification is problematic: when the scalpel is not especially close
to a mesh feature, it may not be possible to match the mesh topology to the
scalpel path without introducing degeneracies.
Our second approach applies to triangulated surfaces. The technique
could be applied to surgery simulation for membrane-like structures,
such as skin or intestine. The method keeps the mesh size and quality
at the initial level through a careful scheme of edge flips, node deletions,
and node insertions. When cutting, a node of the mesh is attached to
the virtual scalpel. Roughly speaking, our method deletes nodes that
are to close to this (moving) active node to prevent degeneracies,
it flips edges around the active node to increase the mesh quality,
and inserts nodes behind the active node to adequately approximate
the past trajectory of the scalpel. We have implemented our approach
and it turns out that it maintains the mesh quality and keeps the mesh
size low, without introducing degeneracies.
Finally, we report some initial results on our approach to needle
insertion.
Simon K. Warfield, Kelly H. Zou and William M. Wells, Harvard University
STAPLE (Simultaneous Truth and Performance Level Estimation) : A New
Validation Algorithm for Judging Image Segmentations
The extraction of geometry from medical images depends upon accurate
image segmentation to appropriately identify the structures of interest.
Characterizing the performance of image segmentation approaches has
been a persistent challenge. Performance analysis is important since
segmentation algorithms often have limited accuracy and precision.
Interactive drawing of the desired segmentation
by domain experts has often been the only acceptable approach, and yet
suffers from intra-expert and inter-expert variability.
Automated algorithms have been sought in order to remove the variability
introduced by experts, but automated algorithms must be assessed to ensure
they are suitable for the task.
The accuracy of segmentations of medical images has been difficult to
quantify in the absence of a known true segmentation for clinical data.
Although physical and digital phantoms can be constructed for which
``ground truth'' is known or readily estimated, such phantoms don't fully
reflect clinical images in that it is difficult to construct phantoms which
reproduce the full range of imaging characteristics and normal and
pathological anatomical variability observed in clinical data.
Comparison to a collection of segmentations by experts is an attractive
alternative since it can be carried out directly on the clinical imaging
data for which the validation of the segmentation is desired, but the most
appropriate measure or measures with which to compare such segmentations has
not been clarified and several measures are used in practice.
We present here an Expectation-Maximization algorithm we call STAPLE
(Simultaneous Truth and Performance Level Estimation). The algorithm takes
a collection of segmentations and computes a probabilistic estimate of the
true segmentation and a measure of the performance level represented by each
segmentation. The source of each segmentation in the collection may be
an appropriately trained human expert or experts, or it may be an automated
segmentation algorithm. STAPLE is straightforward to apply
to clinical imaging data, it readily enables the validation of an automated
image segmentation algorithm, and allows direct comparison of expert and
algorithm performance.
Illustrative results are presented on digital phantoms for which the true
segmentation is known, and for several clinical applications that require
validation of image segmentations.
Cedric Yu, University of Maryland School of Medicine
Mathematical and Algorithmic Challenges in Radiotherapy
In the talk, I will review the current topics and discuss what we are doing
at the University of Maryland School of Medicine. These include IMRT
optimization, brachytherapy optimization, deformable image registration
using an optimization setting and a clinical trial related to it,
and IGS/CAS/CAD (computer aided diagnosis). I will introduce the problems
and the current status. I will also talk about dose calculation, which has
been always a compromise between accuracy and computational speed. There
could also be an algorithmic solution for the dose calculation problem.
In the second part of my talk, I would like to touch some new areas that
are not on our current screen. These include genomics and proteomics,
biological modeling, and simulation of radiation induced DNA damage and
repair. I will illustrate that the new possibilities are much broader than
in the traditional areas.
Eva Lee, Georgia Institute of Technology and Emory University School of Medicine
(joint work with Tim Fox and Ian Crocker, Emory University School of Medicine)
Beam Geometry and Intensity Map Optimization in Intensity-Modulated
Radiation Therapy via Combinatorial Optimization
In this talk, we describe the use of mixed integer programming for simultaneously determining
optimal beamlet .uence weights and beam angles in intensity-modulated-radiation-therapy treatment
planning. In particular, binary variables are used to capture use/non-use of each beam, and
continuous variables capture intensity values for each beamlet. For the tumor, explicit constraints
include coverage with tumor underdose speci.ed, conformity, and homogeneity;while DVH restrictions
for critical structures and normal tissues are imposed. Our algorithmic design thus far
has been motivated by clinical cases. To set up the model, 16-24 coplanar candidate .elds of size
20x20 cm2 are generated, each consisting of 1600 5mm-beamlets. The maximum number of .elds
in the .nal plan will be constrained. Numerical tests are performed and analyzed on three tumor
sites: 1)head-and-neck tonsil, 2)posterior-fossa-boost, and 3)prostate. In all cases, homogeneity is
kept below 1.25, while requiring 95% tumor-volume coverage by the 100% isodose-curve and 100%
tumor-coverage by the 95% isodose-curve. Optimal plans are obtained when maximum number of
.elds are restricted from 6-24 .elds. Sensitivity of quality of plans versus various objective functions
are compared and analyzed. For a practical 8-.eld practical plan, optimal results in the quality of
plans for the head-and-neck tonsil case and the posterior fossa boost occur when the conformity is
minimized in the objective function. In the prostate cancer case, there are overlapping boundary
points in the rectal wall and the prostate, and the best quality plan (for 8-.elds) results from an
objective which minimizes the total weighted dose to the rectum and bladder, together with a tight
ring of 5mm-thick normal tissue drawn around the prostate-PTV. The deviation in best objective
choice use may result from the closeness of the rectal wall (and the bladder) to the prostate with
overlapping boundary points.
Jinhui Xu, Guang Xu, Zhenming Chen and Kenneth R. Hoffmann, SUNY Buffalo
Determining Bi-Plane Imaging Geometry for Reconstructing 3-D
Vascular Structures
 Other Workshops
Other Workshops
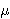 ,
, 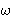 ) is the set of
integer points satisfying a double linear Diophantine
inequality of the form 0 < ax + by +
) is the set of
integer points satisfying a double linear Diophantine
inequality of the form 0 < ax + by + 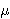 <
< 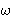 .
Here
.
Here 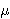
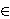 Z is an internal translation constant
measuring the shift of the line with respect to the origin, while
Z is an internal translation constant
measuring the shift of the line with respect to the origin, while 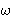
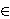 N is the arithmetic thickness
of the line. Respectively, a discrete plane P(a, b, c,
N is the arithmetic thickness
of the line. Respectively, a discrete plane P(a, b, c, 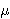 ,
, 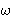 )
is a set of integer points with 0 <
ax+by+cz+
)
is a set of integer points with 0 <
ax+by+cz+ 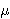 <
< 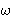 , where the parameters
, where the parameters 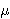
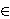 Z and
Z and 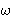
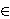 N have similar meaning. L(a, b,
N have similar meaning. L(a, b, 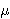 ,
,
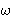 )
and P(a, b, c,
)
and P(a, b, c, 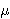 ,
, 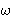 ) can be regarded as a discretization of a line (resp. plane) with coefficients a,
b (resp. a, b, c).
It can be shown that if
) can be regarded as a discretization of a line (resp. plane) with coefficients a,
b (resp. a, b, c).
It can be shown that if 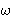 = max(|a|, |b|) (resp.
= max(|a|, |b|) (resp. 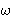 =
max(|a|, |b|, |c|), the above
definitions are equivalent to other well-known classical de.nitions of lines and planes (see [2] for
getting acquainted with di.erent approaches to defining digital straightness, and [3] for a study
on digital flatness).
=
max(|a|, |b|, |c|), the above
definitions are equivalent to other well-known classical de.nitions of lines and planes (see [2] for
getting acquainted with di.erent approaches to defining digital straightness, and [3] for a study
on digital flatness).

 (a, b, c) = max{
(a, b, c) = max{
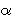 parameter) and
an auxiliary variable z.
parameter) and
an auxiliary variable z.
 f
=
f
= 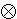 f, where
f, where  Other Workshops
Other Workshops