Radu Balan, Siemens Research
Title: On Frame Redundancy and Measure Functions
Richard Baraniuk, Rice University
Title: Multiscale Edge Grammars for Image Modeling and Processing
Edge singularities play a dominant role in our perception of image
structures. In this talk, we examine the "multiscale edge grammar"
that describes the inter-relationships among wavelet coefficients
required to make up a "valid" edge. The keys to this grammar are the
concepts of "persistence of magnitude" and "coherency of phase" across
scale, which we describe in the complex wavelet domain. A hidden
Markov tree model approximating the edge grammar can easily
discriminate between the large magnitude wavelet coefficients caused
by edges and those caused by texture regions.
For more details, see dsp.rice.edu/publications
Carlos Cabrelli and Ursula Molter, University of Buenos Aires
Title: Shift Invariant Spaces and Homogeneous Functions
In this talk we analyze the structure of shift-invariant spaces.
We consider the case of a single compactly supported refinable generator.
The spectral properties of a finite matrix provide useful information
about the structure of the transition operator, and the assumption of
global linear independence of the integer translates of the generator
allows us to get results on the structure of the shift-invariant space
itself. This information could be potentially useful in the construction
of wavelets, sampling theory in shift invariant spaces, approximation
theory, and many other topics.
Emmanual J. Candes, California Institute of Technology Title: Geometric Multiscale Transforms, Space-Frequency Tilings,
Minimum Total Variation Synthesis The talk will introduce a wealth of new space-frequency tilings which
lead to a new and large family of orthonormal bases for representing
functions of two variables --images. This family of multiscale
transforms is known under the name of the ridgelet packets library and
includes systems such as ridgelets, curvelets and wavelets. Many of
these bases have elements whose envelope is strongly aligned along
specified `ridges' while displaying oscillatory components either
along or across the main `ridge'.
In the second part of the talk, we propose to combine these new
expansions with the Total Variation minimization principle for the
reconstruction of an object whose curvelet coefficients are known
only approximately: quantized, thresholded, noisy coefficients, etc.
We set up a convex optimization problem and seek a reconstruction
that has minimum Total Variation under the constraint that its
coefficients do not exhibit a large discrepancy from the the data
available on the coefficients of the unknown object.
We will present a series of numerical experiments which clearly
demonstrate the remarkable potential of this new methodology for
image compression, image reconstruction and image `de-noising.'
Peter G. Casazza, University of Missouri-Columbia
Title: Custom Building Tight Frames
For applications of frames we generally want two things: (1)
A tight frame (so we do not have to invert the frame operator), and (2)
The frame should satisfy a list of properties needed for our application.
Conventional wisdom had it that tight frames were sparse and therefore
could not be constructed for many applications. We will show that tight
frames are everywhere and we can custom build them for any application
as long as our requirements of the frame satisfy two general principles: (1)
There is a fundamental identity that all tight frames must satisfy and our
properties must not contradict this; and (2) Our properties cannot be too
"rigid" in the sense that frames having our properties cannot be isolated
from all other frames with our property. In this general setting, there are
all the necessary tight frames for applications. Moreover, in the cases where
tight frames having our required properties do not exist, we will identify
the frames which satisfy the properties and are the closest to being tight
(in the sense of minimizing potential energy).
Title: Harmonic Analysis and A/D Conversion
Oversampled A/D conversion, which is one of the most
important practical source coding schemes, effectively
performs irregular sampling of an input bandlimited
signal with a precision equal to the resolution of the
time-discretization of the conversion. In this talk we
present an in-depth study of simple oversampled A/D
conversion using techniques of nonharmonic Fourier
analysis, and derive some new results on irregular
sampling of bandlimited signals which are relevant for
A/D conversion. We use these findings to construct a
single-bit dithered A/D conversion scheme which attains
exponential accuracy in the bit-rate. This is joint work
with I.Daubechies and B.F.Logan
Ingrid Daubechies, Princeton University Title: Redundant representations for A/D conversion Sigma-delta quantizers, used in A/D conversion of bandlimited signals,
give one approach to quantize efficiently highly redundant samples.
Part of the talk will discuss some mathematical properties of and
questions raised by these schemes. In a second part of the talk, a
different type of redundant representation will be discussed, based
on so-called beta-expansions.
The talk presents work by Ron DeVore, Sinan Gunturk, Nguyen Thao,
Vinay Vaishampayan and Ozgur Yilmaz as well as the author.
Matt Fickus, Cornell University
Title: Finite Normalized Tight Frames
In terms of decompositions and reconstructions, tight frames are as
efficient as orthonormal bases, but have the advantage of allowing
redundancy. Normalizing a frame's elements is a natural way in which
to control the size of the frame coefficients. As most applications
of this theory are finite-dimensional, we deal directly with finite
frames to avoid the complications arising from truncation of infinite
frames. We will discuss the theory of finite normalized tight frames
(FNTFs). In particular, we shall demonstrate a connection between FNTFs
and classical concepts of equally distributing points on spheres. The
main result presented will be the characterization of all FNTFs in
terms of the minima of a potential energy function. In addition to
reaffirming the perception of FNTFs as a natural generalization of
orthonormal bases, this result motivates why certain examples of
well-distributed sets, such as the vertices of the Platonic solids or
of the soccer ball, are FNTFs.
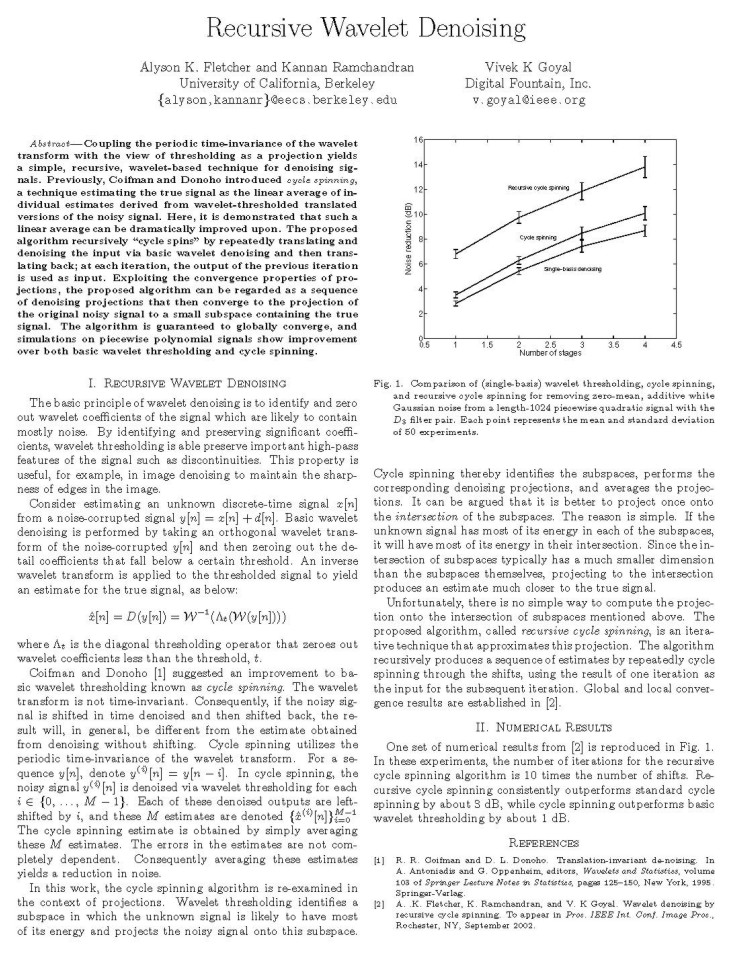
Title: Wavelet Denoising by Recursive Cycle Spinning
Anna Gilbert, AT&T Labs - Research, Shannon Laboratory
Title: Near-Optimal Sparse Fourier Representations via Sampling
A Fourier series decomposes a signal into its trigonometric
components, which vibrate at various frequencies. A B-term Fourier
approximation of a discrete signal s of length N consists of the B
largest Fourier coefficients. We give an algorithm for finding a
Fourier representation r of B terms for a given signal s, such that
the sum-square-error of the representation is within the factor (1 +
epsilon) of best possible error. Our algorithm can access s by reading
its values on a sample set T in [0,N), chosen randomly from a
(non-product) distribution of our choice, independent of s. That is,
we sample non-adaptively. The total time cost of the algorithm is
polynomial in B log(N) log(M) / epsilon (where M is a standard input
precision parameter), which implies a similar bound for the number of
samples. This algorithm has implications for an algorithmic discrete
uncertainty principle and applications to numerical analysis.
Joint work with Sudipto Guha, Piotr Indyk, S. Muthukrishnan, and
Martin Strauss.
Ramesh A. Gopinath, IBM T. J. Watson Research
Title: The Phaselet Transform - An Integral Redundancy Nearly Shift
Invariant Wavelet Transform
This talk introduces an approximately shift invariant redundant dyadic
wavelet transform - the phaselet transform - that includes the popular
dual-tree complex wavelet transform of Kingsbury as a special case.
The main idea is to use a finite set of wavelets that related to each
other in a special way - and hence called phaselets - to achieve
approximate shift-redundancy; bigger the set better the approximation.
A sufficient condition on the associated scaling filters to achieve this
is that they are fractional shifts of each other. Algorithms for the
design of of phaselets with a fixed number vanishing moments are
presented - building upon the work of Selesnick for the design of
wavelet pairs - for Kingsbury's dual-tree complex wavelet transform.
Construction of 2-dimensional directional bases from tensor products of
1-d phaselets is also described.
Vivek K Goyal, Digital Fountain, Inc.
Title: Theorems and Counterexamples in Transform Coding
C. Sinan Gunturk, Courant Institute of Mathematical Sciences, New York University
Title: One-Bit Sigma-Delta Quantization with Exponential Accuracy
C. Heil, School of Mathematics, Georgia Institute of Technology
Radu Balan, Siemens Corporate Research, Princeton, New Jersey
Peter G. Casazza, Department of Mathematics, University of Missouri
Zeph Landau, Mathematical Sciences Research Institute
Title: Excess Frames
An overcomplete frame for a Hilbert space has the property that at
least one element can be removed yet leave a complete set, and in fact
the remaining set must itself be a frame. The excess of the frame is
the greatest integer n such that n elements can be deleted from the
frame and still leave a complete set, or ¥ if there is no upper bound
to the number of elements that can be removed. A frame with finite
excess is a Riesz basis with finitely many extra elements.
We present several related results on frames with infinite excess,
including an explicit characterization of those frames for which
infinitely many elements can be deleted yet leave a frame. We apply
these results to the case of Gabor and wavelet frames with multiple
generators. For these systems, the case of irrationally related
translation parameters requires special care and leaves some
interesting open questions.
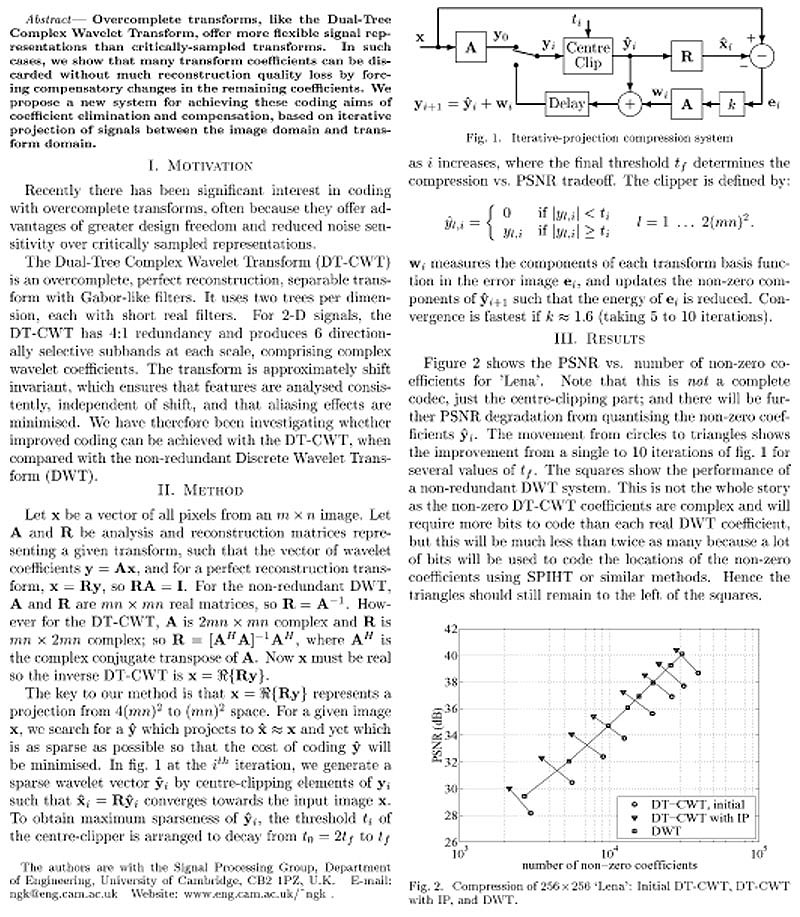
Nick Kingsbury and Tanya Reeves, Signal Processing Group, Department of Engineering, University of Cambridge
Title: Image Compression with Overcomplete Complex Wavelets using Iterative Projection
Ognyan Kounchev, Bulgarian Academy of Scineces / University of Duisburg
Hermann Render, University of Duisburg, Germany
Title: Distributed Filters - Application of Polysplines to Image Processing
We present a new approach to Image Processing based on a new concept
of multivariate splines - polysplines. The last are piecewise
solutions of higher order elliptic equations, in particular
polyharmonic functions, where the pieces join smoothly across some
interfaces (see the monograph of the first author, "Multivariate
Polysplines: Applications to Numerical and Wavelet Analysis", Academic
Press, 2001, some chapters are available in www.math.bas.bg/~kounchev).
The theory of polysplines enjoys direct and nice analogies with the
theory of one-dimensional splines.
The polysplines are very flexible objects: it is possible to choose
the interfaces of the polyspline in an adaptive way, "detecting" the
singularities of the image to be analyzed. One may refine the set of
interfaces by adding new interfaces, and to obtain "polyharmonic"
wavelet analysis. This is completely analogous to the one{dimensional
wavelet analysis through splines where the refinements consist of
adding new knots for the splines. Respectively, one obtains the
"polyharmonic wavelet spaces", and their only generator called
"polywavelet". The amazing thing is that in a large class of interface
configurations it is possible to effectively compute the polywavelets,
and their computation may be reduced to the computation of an infinite
number of (different but very similar) one-dimensional wavelets for an
infinite family of generalized splines, the so-called L-splines(see
L.L. Schumaker, Theory of Splines, Wiley, 1981 ). Let us remark that
the study of the wavelet analysis using L-splines was initiated in the
paper of de Boor, C., DeVore, R., and Ron, A., On the construction
of multivariate (pre)wavelets, Constructive Approximation, 9
(1993), pp. 123-166. If we index all L-splines above through an index
set K; one obtains explicitely an infinite number decomposition and
reconstruction relations, and filters Fk, k Î K,
for all one-dimensional "L-wavelets". Respectively, the polyspline
wavelet analysis is relying upon decomposition and reconstruction
relations and a theory of "distributed filters" F which are
operators decomposed in the infinite number of one{dimensional
filters, i.e. F = ÅkÎK Fk
The polysplines enjoy nice experimental results in data smoothing, so
it might be expected that the polywavelets will perform well in data
compression.
Jelena Kovacevic, Bell Labs, Lucent Technologies
Aurelie C. Lozano, MIT Media Lab
Mike Andrews, Bell Labs, Lucent Technologies
Title: Quantized Frame Expansions in a Wireless Environment
We study frames for robust transmission over a multiple-antenna
wireless system - BLAST. By considering as erased a component received
with an SNR inferior to a given threshold, we place frames in a
setting where some of the ele- ments are deleted. In [1], the authors
focused on the performance of quantized frame expansions up to M-N
erased components, the structure of a frame being thus preserved. In
this paper we consider every possible scenario of erasures for
low-dimensional frames and we present optimal designs for
corresponding systems using a small number of antennas.
I. INTRODUCTION
Transmission of data in a wireless environment must contend with
multipath propagation, a characteristic historically viewed as an
impairment which causes signal fading. BLAST is a communication
technique which exploits the multipath characteristics of the
wireless channel in an efficient manner to enhance capacity. Jerry
Foschini and Mike Gans, worked out a theoretical framework for BLAST
[2]. BLAST assumes a rich scattering environment. It is a single
user system that uses multiple transmitters and receivers, each with
its own antenna, to create a number of parallel subchannels, each
carrying independent data. The transmitted signals all occupy the same
bandwidth simultaneously, so spectral efficiency is roughly
proportional to the number of subchannels. At the receiver, BLAST uses
a combination of linear and nonlinear detection techniques to
disentangle the mutually interfering signals.
This work uses frames to provide robustness against erasures
encountered in the transmission over such a wireless system.
The analysis of a system with a small number of antennas and
therefore with frames of low dimensions leads to optimal designs
minimizing the mean-square error.
II. QUANTIZED FRAME EXPANSIONS WITH ERASURES
Frames, providing redundant representations in contrast to
bases, have been used in diverse areas for different reasons.
They provide resilience to additive noise [3], resilience to
quantization [1], numerical stability of reconstruction [3], and greater
freedom to capture significant signal characteristics [4], [5]. The
redundancy of a frame can also mitigate the effect of losses in
packet-based communication systems [1]. A good introduction
to frames can be found in [3, Ch. 3].
The signal vector x Î RN is expanded with a frame operator
F to give the frame coefficient vector y Î RM. The scalar quantization
of y gives ý, which is transmitted over a BLAST system
with M transmit and M receive antennas. We then assume that
some of the components are erased. A reconstruction x Î RN
is computed from the received vector z.
The transmission is organized around a system using BLAST
with M transmit and M receive antennas. According to the
SNRs coming from the M transmitters, we decide to abstract
the effect of the transmission as erasures of some components of
ý. We systematically discard a component if the SNR is below
a given threshold.
The decoder receives only M-e of the quantized output sequences,
where e is the number of erasures during the transmission. In [1]
it was assumed that there were no more than M-N erasures. To
analyze the case with more than M-N erasures, we need a statistical
model for the input sequence. We thus consider the source x to be
a zero-mean, white, Gaussian vector with covariance matrix
Rx s2IN. We use entropy-coded unifor quatization (ECUQ). We denote the
distortion-rate performance of ECUQ on a gaussian varable with
variance s2 by Ds2(R). For coding at a total rate of R bits per
component of x, NR bits are split among M descriptions. Thus the
quantization noise power sh is equal to Ds2(NR/M). The reconstruction
process is linear and uses the pseudoinverse of the frame operator.
For more details about quantization and reconstruction, the
reader is encouraged to consult [1].
We ultimately want to design frames that give good MSE
performance, so as the first step, we compute the effect of erasures
on the MSE, considering both the cases when the structure of
the frame is preserved and when the number of erasures being
too large, we do not have a frame anymore. We then concentrate
on optimizing the frame design in systems with a small
number of antennas; in particular, we study the optimization of
3x2 frames in a system with 3 transmit and 3 receive antennas.
More details on this work can be found in [6].
REFERENCES:
[1] V.K Goyal, J. Kovacevic, and J.A. Kelner. Quantized frame expansions
with erasures. Journal of Appl. and Comput. Harmonic Analysis,
10(3):203-233, May 2001.
[2] G.J. Foschini and M.J. Gans. On the limits of wireless communications
in a fading environment when using multiple antennas. Wireless Personal
Comm., 6(3):311-335, March 1998.
[3] I. Daubechies. Ten Lectures on Wavelets. SIAM, Philadelphia, PA, 1992.
[4] J.J. Benedetto and G.E. Pfander. Wavelet periodicity detection algorithms.
In Proc. SPIE Conf. on Wavelet Appl. in Signal and Image Proc.,
pages 48-55, San Diego, CA, July 1998.
[5] M. Unser. Texture classification and segmentation using wavelet frames.
IEEE Trans. Image Proc., 4:1549-1560, November 1995.
[6] A. Lozano, J. Kovacevic, and M. Andrews. Quantized frame
expansions in a wireless environment. In Proc. Data Compr. Conf.,
Snowbird, Utah, March 2002.
Z. Landau, University of California, Berkeley
Title: Density of Frames
The decomposition of signals as a linear combination of some fixed
set of vectors V is at the heart of most techniques in signal
processing. The most common choice of V is a basis for the space of
signals; such a situation produces a unique decomposition for any
signal. However, picking an overcomplete set of vectors for V can be
advantageous: from the many ways to decompose a given signal, a choice
can be made that is "efficient" (according to some definition).
Frames are choices for V that are overcomplete but that otherwise
resemble bases; specifically, a collection of vectors V = {fi}
is said to be a frame for a Hilbert space H, if there exist
positive constants A and B such that
Stephane Mallat, Courant Institute, New York University
Erwan Le Pennec, Ecole Polytechnique, France
Title: Sparse Geometrical Image Representations with Bandelets
Finding sparse representations is at the core of image processing for
applications such as compression, restoration or pattern recognition.
Despite their success, wavelets are far from optimal since they can not
take advantage of existing geometrical regularities in images.
Incorporating geometry in harmonic analysis representations such as
wavelets is also an important step to bridge the gap between classical
image processing which often represent images in bases, and computer
vision which analyzes image information with geometric representations.
Bandelets are orthonormal bases whose vectors are adapted to follow the
geometrical regularity of images. This geometry is defined by a vector
field that indicates the local directions along which the image has
regular variations. For images including singularities that are along
regular curves, it is proved that the error of a non-linear approximation
in a bandelet basis has an optimal decay rate, which is not achieved by
wavelet bases. Numerical examples compare the performance of bandelet
and wavelet representations. We shall describe an application to noise
removal with thresholding estimators and discuss applications to image
compression.
Antonio Ortega, University of Southern California
Title: Application-specific lossy signal compression for distributed signal processing
Most of the work to date on signal compression, both practical and
theoretical, has focused on coding a signals based on fidelity
criteria. The underlying assumption is that signals are compressed so
as to be stored or transmitted, and ultimately rendered.
Ubiquitous wired or wireless access to networks and the decreasing
cost of signal acquisition equipment (e.g. video cameras), make it
likely that distributed signal processing system will become popular
(consider for example, sensor networks, distributed multimedia
databases, etc).
Many of these distributed systems will be such that signal processing
and acquisition are not co-located, so signal data needs to be
transfered, preferably in compressed format. A common characteristic
in these scenarios is that signals to be compressed will not be
stored or displayed in their entirety; instead, decoded signals will
be processed, and then discarded. Thus, the main objective of encoding
algorithms used in this context should be to use as few bits as possible,
without altering the outcome of the processing, as compared to
processing performed on the original (non-compressed) data.
In this talk we present several examples of our recent work into
application-specific compression, where non-standard criteria are used
to optimize the compression performance. In particular we provide
examples in distributed speech recognition, distributed image
acquisition for a centralized database storage, distributed acoustic
source localization, and distributed control of a simple robot.
P. Oswald, Bell Labs, Lucent Technologies
Title: Smoothness of nonlinear subdivision based on median interpolation
We give a refined analysis of the Holder regularity for the limit
functions arising from a nonlinear pyramid algorithm proposed by
Donoho and Yu [1] for triadic refinement. Although the work in [1]
is motivated by applications to robust removal of non-Gaussian noise,
the Donoho-Yu scheme can be interpreted as a nonlinear subdivision
process where new points are inserted based on local quadratic
polynomial median interpolation.
We introduce an analogon of the Donoho-Yu method for dyadic
refinement, and show that its limit functions are in Ca for some
a > 1. In the triadic case, we improve the previously known lower
bound of a > log3(135/121) = 0.0997... to a > log3(135/53) =
0.8510... The improved bounds are the result of deriving recursive
inequalities for second rather than first order differences, and
they are close to the conjectured exact values. We also discuss some
closely related nonlinear subdivision schemes. Our case study [2]
hopefully fuels further interest in some open conjectures concerning
nonlinear subdivision processes and their relationship with linear
schemes.
[1] Donoho D. and T. P.-Y. Yu, Nonlinear pyramid transforms based on
median interpolation, SIAM J. Math. Anal. 31 (2000), 1030-1061.
[2] Oswald, P., Smoothness of nonlinear median-interpolation subdivision,
tech. report, Bell Labs, Lucent Technologies, Murray Hill, NJ (2002).
Justin K. Romberg, Michael B. Wakin, Hyeokho Choi, Richard G. Baraniuk,
Dept. of Electrical and Computer Engineering Rice University
Title: Geometric Modeling of Edges in Images
Many of today's most successful image coders rely on
wavelets to represent the signal. This is in spite of
the fact that wavelets offer an inefficient representation of
edges, which are commonly occurring and dominant
features in most images. Consider, for example, a single
straight edge separating two grayscale regions in an
image. This object is low-dimensional - it can be
parameterized (or coded) using only 4 parameters (orientation,
offset, and the two grayscale values) - but the number of
wavelet coefficients necessary to describe the edge grows
as the number of pixels crossed by the edge. Similar
arguments can be made for curved edges, where the contour
admits a low-dimensional representation. Most wavelet-based
coding techniques exploit some dependency among these
wavelet coefficients, typically a persistence of their
magnitude through scale and space. However, the most salient
information about images of this type is not what values
the significant wavelet coefficients are taking, but which
wavelet coefficients are taking these values - the trace of
the contour in the plane tells us more about the image than
the height of the jump between the two regions. Since the
contours in real world images are smooth, the locations of
the significant coefficients are heavily dependent from scale
to scale.
We propose a spatial-domain multiscale geometry model
that succinctly describes an edge contour by exploiting its
smoothness in space, allowing for efficient compression of
edge information. As an application of the model, we
consider describing the class of images consisting of two
constant regions separated by a contour (the so called
"Horizon" class of images) using a discrete set of linear wedgelet
functions [1]. A wedgelet is essentially a picture of a
straight edge, which can be at a number of different
orientations, passing through a dyadic block of pixels. Wedgelets
of various sizes and orientations can be aligned along an
edge contour to provide a piecewise linear approximation
of the curve. Fast algorithms exist for finding wedgelets
at various scales (various size dyadic blocks) to efficiently
represent horizon class images in the sense of asymptotic
approximation rate [1], and asymptotic rate-distortion
decay [2]. In addition, fast algorithms exist for the
calculation of wedgelet projection coefficients when the wedgelet
dictionary is properly restricted [3].
Since the curves in the horizon class of images are
smooth, the orientations of the wedgelets used in different
dyadic blocks in an efficient representation will exhibit
dependencies. For example, we expect that wedgelets located
near each other will be at about the same orientation. The
purpose of the multiscale geometry model, in this case, is
to describe these dependencies. Our modeling framework
uses a quadtree Markov structure: the orientations of the
four wedgelets used to describe the image in each
quadrant of a subdivided dyadic block, are related to each other
through the orientation of the wedgelet that describes the
image over the whole dyadic block. In an extreme case,
this modeling framework can even be used to produce best
connected wedgelet chains at a given scale. The Markov
structure allows fast optimization algorithms, and can be
directly incorporated into the wedgelet selection algorithms
in [1] and [2].
A complete geometry model for a class of curves should
ultimately lead to more efficient compression of natural
images. Wavelets, for example, could still be used for
smooth and textured regions, while a methodology such as
wedgelets could be used to efficiently represent the
dominant edges. A current research topic for the authors is
combining edge orientation information into practical wavelet
coding schemes, see [4], for example. The successful
combination of these strategies will require geometry models
that are accurate, practical, and can be incorporated into
wavelet coders in such a way that optimal trade-offs
between coding edges and texture can be made; all of these
are properties of the model presented here.
REFERENCES
[1] D. Donoho, "Wedgelets: Nearly-minimax estimation of edges,"
Annals of Stat., vol. 27, pp. 859-897, 1999.
[2] M. N. Do, P. L. Dragotti, R. Shukla, and M. Vetterli, "On
the compression of two-dimensional piecewise smooth functions,"
in IEEE Int. Conf. on Image Proc. - ICIP '01, Thessaloniki,
Greece, Oct. 2001.
[3] J. K. Romberg, M. B. Wakin, and R. G. Baraniuk, "Multiscale
wedgelet image analysis: fast decompositions and modeling," in
IEEE Int. Conf. on Image Proc. - ICIP '02, 2002, Submitted.
[4] M. B. Wakin, J. K. Romberg, H. Choi, and R. G. Baraniuk,
"Rate-distortion optimized image compression using wedgelets,"
in IEEE Int. Conf. on Image Proc. - ICIP '02, 2002, Submitted.
Ivan Selesnick and Levent Sendur, Electrical and Computer Engineering, Polytechnic University
Title: Bivariate Probability Models and Shrinkage Functions
We propose a new simple non-Gaussian bivariate probability
distribution function to model the statistics of wavelet coefficients
of natural images. The model captures the dependence between a wavelet
coefficient and its parent. Using Bayesian estimation theory we
derive from this model a simple non-linear shrinkage function for
wavelet denoising, which generalizes the soft thresholding approach of
Donoho and Johnstone. The new shrinkage function, which depends on
both the coefficient and its parent, yields improved results for
wavelet-based image denoising.
Let w2 represent the parent of w1 (w2 is the wavelet coefficient at
the same spatial position as w1, but at the next coarser scale). Then
y = w + n (1)
where w = (w1;w2), y = (y1; y2) and n = (n1; n2). The noise values n1;
n2 are iid zero-mean Gaussian with variance s2n. We propose the
following non-Gaussian bivariate pdf
(2)
Emina Soljanin, Bell Labs, Lucent
Gilbert Strang and Per-Olof Persson, MIT
Title: Filtering and Signal Processing
We discuss two filters that are frequently used to smooth data.
One is the (nonlinear) median filter, that chooses the median of
the sample values in the sliding window. This deals effectively
with "outliers" that are beyond the correct sample range, and will
never be chosen as the median. A straightforward implementation of
the filter is expensive for large windows, particularly in two
dimensions (for images).
The second filter is linear, and known as "Savitzky-Golay". It is
frequently used in spectroscopy, to locate positions and peaks and
widths of spectral lines. This filter is based on a least-squares fit
of the samples in the sliding window to a polynomial of relatively
low degree. The filter coefficients are unlike the equiripple filter
that is optimal in the maximum norm, and the "maxflat" filters that
are central in wavelet constructions. Should they be better known....?
We will discuss the analysis and the implementation of both filters.


Alyson Fletcher, University of California Berkeley


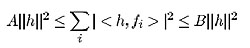 for all vectors h Î H.
Often one tries to use the general structure of the signals to guide the
choice of vectors fi for the frame. This is the case in Weyl-Heisenberg and
wavelet systems where one sets the fi to be shifts in time and frequency of
a single vector (Weyl-Heisenberg) or dilates and shifts in time of a single
vector (wavelet).
In the case of Weyl-Heisenberg systems, a beautiful density result gives
a necessary condition for the system {e2paitf(t-bi)}to be a frame in terms
of the density of the points (ai, bi) in the plane. In this talk we'll give a
general notion of density for frames (not necessarily Weyl-Heisenberg) and
relate frame density to frame span. This work extends and unifies most of
the known density results about frames.
(joint work with R. Balan, P. Casazza, C. Heil)
for all vectors h Î H.
Often one tries to use the general structure of the signals to guide the
choice of vectors fi for the frame. This is the case in Weyl-Heisenberg and
wavelet systems where one sets the fi to be shifts in time and frequency of
a single vector (Weyl-Heisenberg) or dilates and shifts in time of a single
vector (wavelet).
In the case of Weyl-Heisenberg systems, a beautiful density result gives
a necessary condition for the system {e2paitf(t-bi)}to be a frame in terms
of the density of the points (ai, bi) in the plane. In this talk we'll give a
general notion of density for frames (not necessarily Weyl-Heisenberg) and
relate frame density to frame span. This work extends and unifies most of
the known density results about frames.
(joint work with R. Balan, P. Casazza, C. Heil)
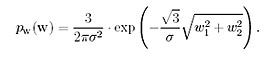 It is not a bad match to empirical bivariate histograms we have
computed. With this pdf, w1 and w2 are uncorrelated, but not
independent. The MAP estimator of w1 yields the following bivariate
shrinkage function
(3)
It is not a bad match to empirical bivariate histograms we have
computed. With this pdf, w1 and w2 are uncorrelated, but not
independent. The MAP estimator of w1 yields the following bivariate
shrinkage function
(3)
 For this bivariate shrinkage function, the smaller the parent value,
the greater the shrinkage. This is consistent with what is known, but
here it is derived using a Bayesian estimation approach beginning with
the new bivariate non-Gaussian model.
For this bivariate shrinkage function, the smaller the parent value,
the greater the shrinkage. This is consistent with what is known, but
here it is derived using a Bayesian estimation approach beginning with
the new bivariate non-Gaussian model.



