

Next: Comparison with BAN logic
Up: The logic
Previous: The language
For the axiomatisation we need to define the contents of a message
as the collection of submessages when encryption is transparent:
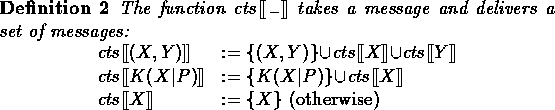
The axiomatisation includes the standard axioms for equational logic
with Modus Ponens -- which subsumes propositional logic --
and the standard rules for universal quantification,
where a formula 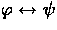 is treated as
shorthand for
is treated as
shorthand for 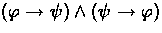 .
.
Beneath, we introduce a collection of axioms for the
specific operators of our logic, and mention
the related axiom in the original BAN logic -- if such an axiom exists.
(Because of the presence of the Modus Ponens rule, we can
replace inference rules
(20,12)[l]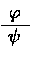 by axioms
by axioms 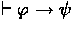 .)
.)
For message joining there are all axioms of the forms
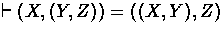 ,
,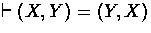 and
and
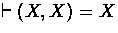 , and for the
, and for the 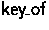 operator
operator
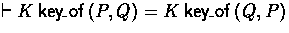 .Equational logic allows us to apply theorems of the form
.Equational logic allows us to apply theorems of the form
![$\derives \phi[x] \land x=y \:\implies\: \phi[y]$](img44.gif) .
.
Furthermore, we have:
- Rationality
- The rationality rule introduces a collection of
axioms, one for every theorem of the logic:

This axiom, together with the next one, lifts the level of
reasoning from beliefs of principals to general statements.
- Believing Modus Ponens
- Modus Ponens under the
 operator:
operator:
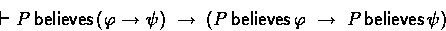
- Saying parts of a joint message
- Uttering a joint message implies uttering each of the parts:
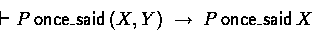
The related BAN logic axiom is:
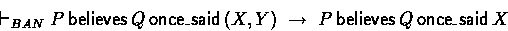
- Saying contents of an encrypted message
- Uttering an encrypted message, signed by yourself, while you believe
that the key is good, implies uttering of the encrypted message:
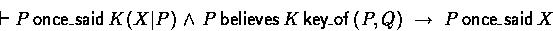
There is no similar axiom in BAN logic.
- Seeing parts of a joint message
- Seeing a joint message means seeing each part separately as well:
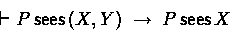
The BAN logic has this axiom (exactly so) as well.
- Awareness
- Awareness of what one sees:
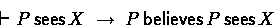
There is no similar axiom in BAN logic.
- Possessing keys of a seen key statement
- If one sees a key statement, one possesses the key that it mentioned:
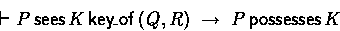
In BAN logic, the notion of possession does not exist.
- Possessing believed keys
- One can only believe that a certain key is good if possessing the key:
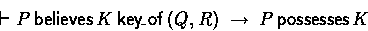
- Decryption
- Seeing an encrypted message while having the key in possession, means seeing
the message itself:

The related BAN logic axiom is decryption:
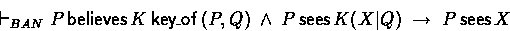 In BAN logic one can only decrypt with keys that are believed to be
one's own key. With any other key in possession, decryption cannot be
derived, since BAN logic does not have a notion of possession.
In BAN logic one can only decrypt with keys that are believed to be
one's own key. With any other key in possession, decryption cannot be
derived, since BAN logic does not have a notion of possession.
- Good key ensures the utterer
- A collection of axioms, stating that if a key is good, the only ones that
use it for encryption are the owners, so if somewhere, someone sees a
message that contains a part encrypted with that key, that
part must have been said by the key owner who encrypted it:
For all P,Q,R,X,Y,K such that 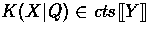 :
:
The related BAN logic axiom is the message meaning rule:
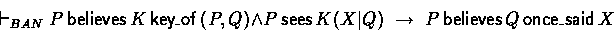
The BAN axioms that were not mentioned above are:

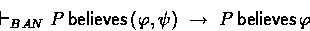
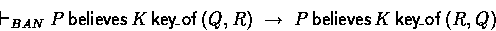
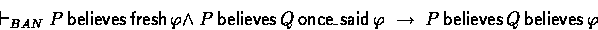
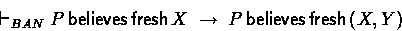
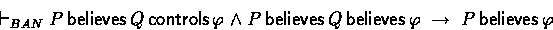


Next: Comparison with BAN logic
Up: The logic
Previous: The language
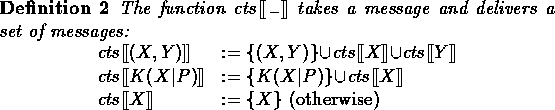
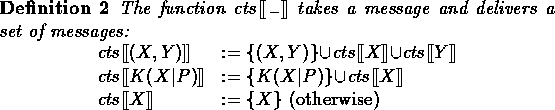
![]() is treated as
shorthand for
is treated as
shorthand for ![]() .
.![]() by axioms
by axioms ![]() .)
.)
![]() ,
,![]() and
and
![]() , and for the
, and for the ![]() operator
operator
![]() .Equational logic allows us to apply theorems of the form
.Equational logic allows us to apply theorems of the form
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]() In BAN logic one can only decrypt with keys that are believed to be
one's own key. With any other key in possession, decryption cannot be
derived, since BAN logic does not have a notion of possession.
In BAN logic one can only decrypt with keys that are believed to be
one's own key. With any other key in possession, decryption cannot be
derived, since BAN logic does not have a notion of possession.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()