The rectify operation ![]() maps formulas to
formulas.
In particular, it maps formulas of the form
maps formulas to
formulas.
In particular, it maps formulas of the form
![]() to
to ![]() .It is defined as follows:
.It is defined as follows:
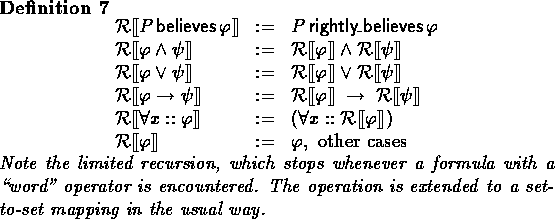
Directly from the definition on sets it follows that:
Proof
We prove it with structural induction on the derivation.
Case trivial proof:
A trivial proof is a derivation step of the form
![]() , where
, where ![]() .
.

Case deduction: Deduction is the introduction of implication by derivation:
If, then
.
Using deduction, we may instantiate:
If, then
.
From here we can derive, under the assumption
![]() :
:
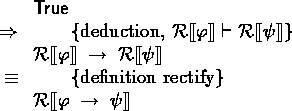
Cases axioms of predicate logic:
As an example, we prove our claim for the introduction of ![]() .Other introductions and eliminations
(
.Other introductions and eliminations
(![]() ,
, ![]() ,
, ![]() ,
, ![]() )have analogous proofs.
)have analogous proofs.

Case Rationality:
Let ![]() .
We prove
.
We prove ![]() .
.

Case axiom:
For every axiom ![]() , we will prove
, we will prove
![]() , by deriving
, by deriving
![]() .
.
case Believing Modus Ponens:
We prove it for the equivalent form
![]()
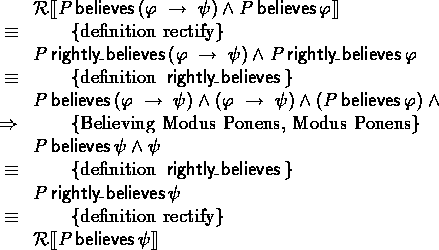
case Saying contents of an encrypted message:

case Awareness:

case Possessing believed keys:
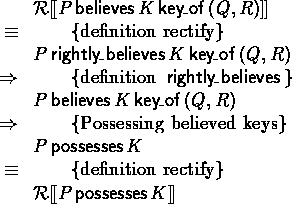
The remaining axioms do not contain a believe operator, so they do not change under the rectify function.
![]()