We define the relation ![]() between states and
formulas (where
between states and
formulas (where ![]() means: in state s formula
means: in state s formula
![]() holds) inductively
on the structure of formulas as the least relation
satisfying:
holds) inductively
on the structure of formulas as the least relation
satisfying:
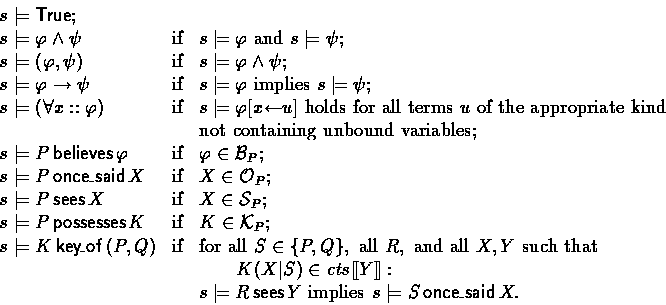
The notation ![]() above means:
above means: ![]() with u
substituted for the free occurrences of x .
If
with u
substituted for the free occurrences of x .
If ![]() , the whole formula
, the whole formula
![]() may be substituted for
may be substituted for ![]() , and since
, and since
![]() , the ``recursion'' in the
definition of
, the ``recursion'' in the
definition of ![]() is unbounded, whence the appeal
above to ``least relation''.
is unbounded, whence the appeal
above to ``least relation''.
Note that the relation ![]() is not monotonic in its
left argument, i.e.,
when
is not monotonic in its
left argument, i.e.,
when ![]() ,
, ![]() does in general not imply
does in general not imply
![]() .
.