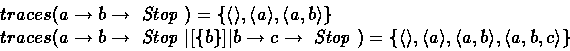
In [Sch96], the traces model is used as the basis for the proof rules presented. In this model, the semantics of a process P is defined to be the set of traces (sequences of events) that it may possibly perform. For example,
A useful operator on traces is projection: If D is a set of events
then the trace ![]() is defined to be the maximal
subsequence of tr all of whose events are drawn from D . If D is
a singleton set
is defined to be the maximal
subsequence of tr all of whose events are drawn from D . If D is
a singleton set ![]() then we overload notation and write
then we overload notation and write
![]() for
for ![]() . Message extraction
. Message extraction ![]() for a set of channel names C provides the maximal sequence of
messages passed on channels C . Finally,
for a set of channel names C provides the maximal sequence of
messages passed on channels C . Finally, ![]() provides the set
of messages in tr passed along some channel in C . These may be
described inductively on sequences, and the last by a set
comprehension:
provides the set
of messages in tr passed along some channel in C . These may be
described inductively on sequences, and the last by a set
comprehension:
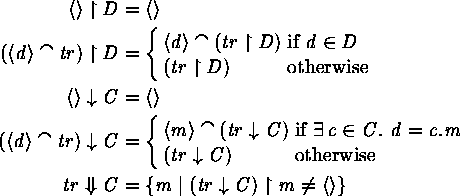
If tr is a sequence, then ![]() is the set of events appearing in the
sequence. The operator
is the set of events appearing in the
sequence. The operator ![]() extends to processes:
extends to processes: ![]() is the set
of events that appear in some trace of P .
is the set
of events that appear in some trace of P .
In the traces model, if ![]() then we say
that Q is a refinement of P , written
then we say
that Q is a refinement of P , written ![]() .
.