Security requirements for real-life applications still increase. For this purpose, many people develop cryptographic protocols in order to fulfill these needs.
When someone designs a new protocol, he usually uses cryptographic tools for which he is confident. The design and the analysis of these tools is the domain of the mathematician and the cryptographer. In many cases, a cryptoalgorithm is proved as secure as solving hard problems (e.g., factoring large composite numbers). No such ``proofs'' exist for the cryptanalysis of protocols. By definition, a protocol designer must suspect everything. The use of strong cryptoalgorithms is not sufficient to guarantee the security of a protocol. In some situations, a protocol may be completely subverted without compromising the security of the underpinning cryptoalgorithm. Such situations are called protocol failures [11].
Protocols are for example designed in order to establish a session
key, to authenticate a transaction, to sign a document, etc...
This is usually achieved by exchanging some messages between two or
several people. In the sequel, we will show a failure on the most
widely used public-key cryptosystem, the so-called RSA [13].
It may be briefly described as follows. Suppose that Alice wants to
send a message m to Bob. To setup the system, Bob carefully selects
two large primes p and q , computes ![]() , chooses a
encryption key
, chooses a
encryption key ![]() relatively prime to
relatively prime to ![]() , and
computes the decryption key
, and
computes the decryption key ![]() according to
according to ![]() . The public key of Bob is the pair
. The public key of Bob is the pair
![]() and his secret key is
and his secret key is ![]() . To send m to
Bob, Alice forms the ciphertext
. To send m to
Bob, Alice forms the ciphertext ![]() and
sends it to Bob. Then, Bob recovers the plaintext by computing
and
sends it to Bob. Then, Bob recovers the plaintext by computing
![]() with his secret key
with his secret key ![]() . The
security of this scheme relies on the intractability to factor
. The
security of this scheme relies on the intractability to factor
![]() . The aim of a pirate, say Carol, is to recover m . This
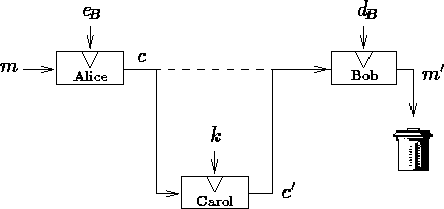
can be done as follows. Carol chooses a random number k , intercepts
c , replaces it by
. The aim of a pirate, say Carol, is to recover m . This
can be done as follows. Carol chooses a random number k , intercepts
c , replaces it by ![]() , and sends c' to
Bob. Now, when Bob deciphers c' , he obtains
, and sends c' to
Bob. Now, when Bob deciphers c' , he obtains ![]() . Since m' is meaningless,
Bob discards it. If Carol can get access to this discard, she finds
. Since m' is meaningless,
Bob discards it. If Carol can get access to this discard, she finds
![]() . This failure was first pointed out by
Davida [5]. Avoiding this attack is easy, the users have to
really destroy the discards, or in other words to protect their bins.
The lesson of this failure is that the protocol designer has to pay
attention to what is generally accepted but not explicitly stated.
. This failure was first pointed out by
Davida [5]. Avoiding this attack is easy, the users have to
really destroy the discards, or in other words to protect their bins.
The lesson of this failure is that the protocol designer has to pay
attention to what is generally accepted but not explicitly stated.
The decryption process can be speeded up by the Chinese Remainder
Theorem (CRT). From p and q , Bob computes
![]() and
and
![]() , and finally finds
, and finally finds
![]() [12]. Suppose that Carol induces an external
constraint on the deciphering device of Bob (e.g., ionizing or
microwave radiation). Assume that the computation of
[12]. Suppose that Carol induces an external
constraint on the deciphering device of Bob (e.g., ionizing or
microwave radiation). Assume that the computation of ![]() is
correctly performed but not computation of
is
correctly performed but not computation of ![]() . So, Bob gets
. So, Bob gets
![]() instead of m . If Bob discards m' and if Carol
can get access to m' , then she finds the secret factor p by
computing
instead of m . If Bob discards m' and if Carol
can get access to m' , then she finds the secret factor p by
computing ![]() . Hence,
. Hence,
![]() and Carol can compute the secret decryption key
and Carol can compute the secret decryption key
![]() [10,7].
[10,7].
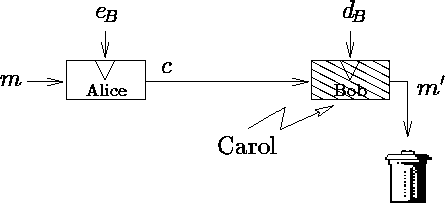
This second attack is more dangerous because it completely breaks the system. This shows clearly the importance of checking cryptographic protocols for faults [3]. Note also that if Bob protects his bin, the attack does not remain applicable.
The two previous attacks show that it is extremely difficult for a protocol designer to determine whether his protocol is sound, even for very simple protocols. Some researchers proposed formal techniques for analyzing the soundness of protocols, such as the BAN logic [4] or the three systems presented in [8].
Another approach for the protocol designer is to try to find flaws in his protocol with all his experience of good and bad practice. In [1], Abadi and Needham give general rules helping protocol designers to avoid many of the pitfalls (see also [2]). In this paper, we push their work further, and show that the protocol designers must also take care about the hardware and software implementation of the protocol.