Introduction to Posets
By
Tom Trotter
Arizona State University





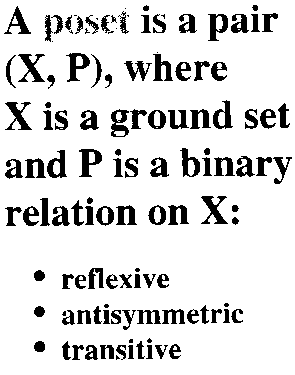

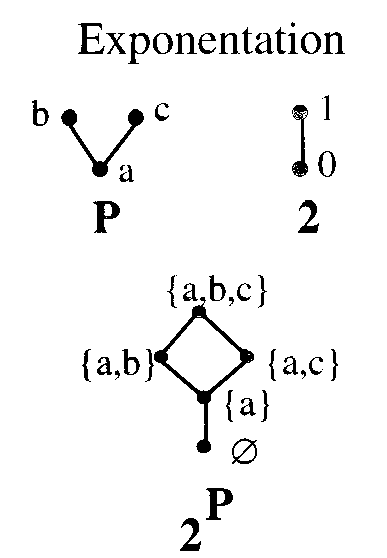


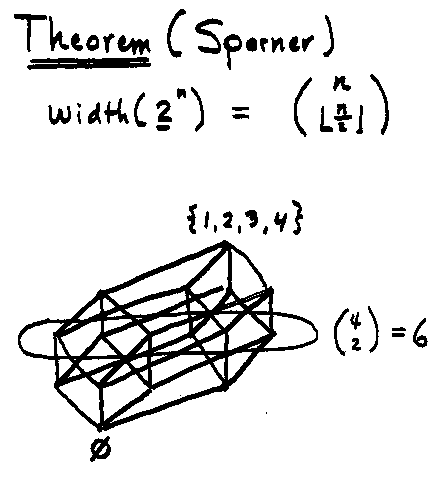
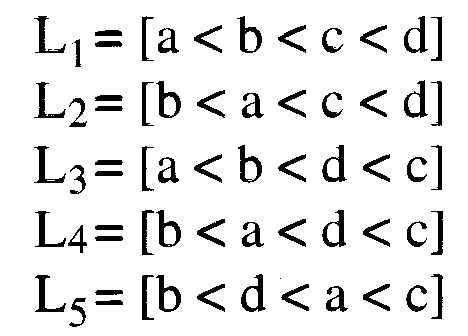
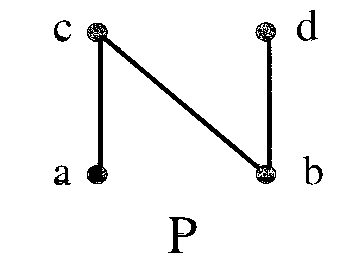

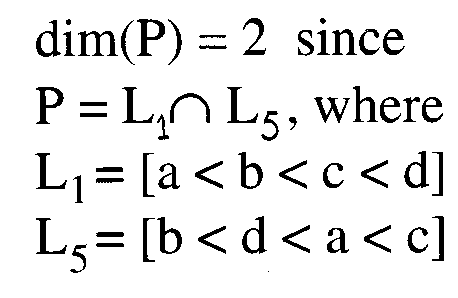
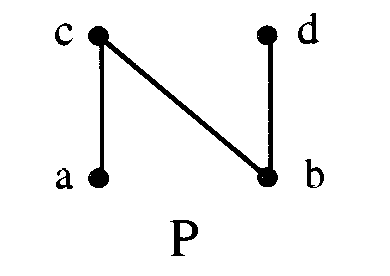


Alternate Definition
Definition. Alternatively, dim(P) is the least t so that
P is isomorphic to a:

Theorem
(W. Schnyder'89)
G is planar
iff
dim P(G) <= 3
The Incidence Poset of a Graph
Definition. Given a graph G = (V, E), we associate a poset whose ground set is V U E. The order is defined by x < S if and only if xE V, SEE andxES.

A Probability Space
The probability, that x < y in P, denoted Pr[x < y], is the number of linear extensions with x < y over the total number of linear
extensions.
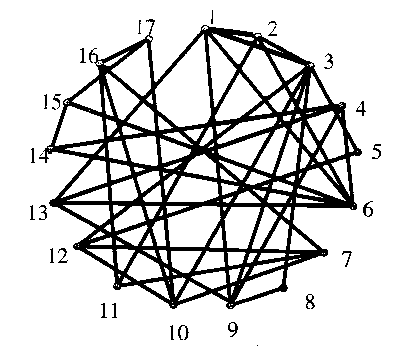
Example
Pr[x < y] = 2/5.

The XYZ Theorem
(Sh.epp '80)
Pr[x > y]<= Pr[x > ylx > z ]
The Strict XYZ Theorem
(Fishburn '84)
If x and z form an antichain,
ichain,
Pr[x > y] < Pr[x > ylx > z ]
The 1/3 - 2/3 Conjecture
(Kislitsyn '66)
If P is a poset which
is no a chain, then there exists X,Y in P so that
1/3 < Pr[x < y] < 2/3
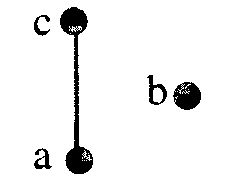
Best possible
If true!
Pr[a < b] = Pr[b < c]= 2/3
Theorem (Kahn, Saks '84)
If P is a poset which
is not a chain, then there
exists X, y in P so that
3/11 < Pr X < y < 8/11
Note.* Proof requires the
Alexandrov/Fenchel inequalities for mixed volumes,.
Theorem (Brightwell, FeIsner and, Trotter '95)
If P is a poset which .
is not a chain, then there exists x, y in P so that
Note: Proof builds on Kahn and Saks approach. Also requires Ahlswede/Daykin Four Function Theorem.
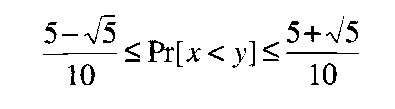
P is isomorphic to a:


Theorem
(W. Schnyder'89)
G is planar
iff
dim P(G) <= 3