THE FIRST FOUR STANDARDSThe First Four Standards - Grades 9-12
OverviewNew Jersey's Mathematics Standards calls for a shift in emphasis from a high school curriculum often dominated by memorization of isolated facts and procedures and by proficiency with paper-and-pencil skills to one that stresses understanding of concepts, multiple representations and connections, mathematical modeling, and mathematical problem solving. The distinction between mathematical problem solving and doing mathematics should begin to blur in the high school grades. The problem-solving strategies learned in the earlier grades should have become increasingly internalized and integrated to form a broad basis for doing mathematics, regardless of the specific topic being addressed. From this perspective, problem solving is much more than solving word problems; it is the process by which mathematical ideas are constructed and reinforced. There is more emphasis in high school on introducing new mathematical concepts and tools as responses to problem situations in mathematics, and on developing students' ability to pose problems themselves. Through extensive experiences with mathematical communication, students improve their understanding of mathematics. Students must be able to describe how they obtain an answer or the difficulties they encounter in trying to solve a problem. Facility with mathematical language enables students to form multiple representations of ideas, express relationships within and among these representations, and form generalizations. High school students should continue to experience two types of mathematical connections - those within mathematics, and those to other areas. First, students should make connections between different mathematical representations of the same concept or process. Students who are able to apply and translate among different representations of the same problem situation or of the same mathematical concept have not only a powerful, flexible set of tools for solving problems but also a deeper appreciation of the consistency and beauty of mathematics. Unifying ideas within mathematics to be emphasized in the high school grades include mathematical modeling, variation (how a change in one thing is associated with a change in another), algorithmic thinking (developing, interpreting, and analyzing mathematicalprocedures), mathematical argumentation, and a continued focus on multiple representations. Second, students in high school should regularly discuss the connections between mathematics and other subjects and the real world. Connections between mathematics and science are particularly plentiful. Examples of such activities are:
A student who is doing mathematics often makes a conjecture by generalizing from a pattern of observations made in specific cases (inductive reasoning) and then tests the conjecture by constructing either a logical verification or a counterexample (deductive reasoning). High school students need to appreciate the role of both forms of reasoning. They should also learn that deductive reasoning is the method by which the validity of a mathematical assertion is finally established. Much inductive reasoning may take place in algebra, with students looking for patterns that arise in number sequences, making conjectures about general algebraic properties based on their observations, and verifying their conjectures with numerical substitutions. Students can be introduced to deductive reasoning by examining everyday situations, such as advertising, in which logic arises. Logical arguments in mathematical situations need not follow any specific format and may be presented orally or in writing in the student's own words. High school students focus on mathematical problem solving, using multiple representations of mathematical concepts, mathematical connections, and reasoning throughout all of their mathematics learning. As they learn and do mathematics, they should regularly encounter situations where they are expected to discuss and solve problems, develop mathematical models, explain their results, and justify their reasoning. The content of these four standards is inextricably interwoven with the fabric of mathematics. On-Line Resources
The First Four Standards - Grade 9-12Vignette - Making RectanglesStandards: In addition to the First Four Standards, this vignette highlights Standards 7 (Spatial Sense), 11 (Patterns), and 13 (Algebra).
The discussion: Mrs. Ellis encouraged the students to share their ideas for how they might go about solving this problem. Some of their questions were: What materials might be helpful in working on this problem? How could we use the algebra tiles? What might be some combinations of tiles that we might try? How could we keep track of what we have tried? Can we use more than one of the red x2 tiles? Will we be able to try out all of the possible combinations? Do you suppose that we will find some sort of pattern that can help us predict which combinations will work and which will not? Solving the problem: The students worked in groups of three or four over a period of three days. They tried different combinations of tiles, recording how many of each tile they used, whether or not that combination could be used to form a rectangle, and, if so, the dimensions of the rectangle. As they worked, they began to notice patterns. Some of their comments were: This seems like multiplying binomials but in reverse. When it works, the product of the number of 1s on the top times the number of 1s on the sides equals the number of yellow unit tiles. If there's just one of the red tiles, then the sum of the number of 1s on the top plus the number of 1s on the side equals the number of orange tiles. Each group summarized its conclusions and the patterns they found in a report. Summary: Mrs. Ellis asked the groups to exchange reports with another group, then read, review, and comment on the other group's report. Each group then had an opportunity to review the comments on their report. Mrs. Ellis asked the students about the patterns they had found. Are there some patterns that both of your groups found? Are there others that only one of the groups found? She recorded the findings on the board. How can we be sure all of these statements are correct? The students suggested that, if everyone agreed with a statement and could justify their reasoning, then it should be accepted as correct. They discussed each of the statements, explaining their reasoning and arguing about some of the statements. For homework, Mrs. Ellis asked the students to use their findings to make some predictions about other combinations of tiles and to relate their results to the idea of factoring binomials. Mrs. Ellis expects that in the next classes she will connect the problem of making a rectangle from a red x2 tiles, b orange x tiles, and c yellow unit tiles to the problem of factoring ax2 + bx + c. The First Four Standards - Grades 9-12Vignette - Ice Cones*Standards: In addition to the First Four Standards, this vignette highlights Standards 6 (Number Sense), 7 (Geometry), 8 (Numerical Operations), 9 (Measurement), 11 (Patterns), 13 (Algebra), and 15 (Building Blocks of Calculus). The problem: Ms. Longhart began class by posing the following problem for her students: Suppose that you are setting up a water ice stand for the summer and are trying to decide how to make the cones in which you will serve the water ice. You've found some circles of radius 10 cm that are the right type of paper and have figured out that by cutting on a radius, you can make cones. You decide that you would like to make cones that hold as much water ice as possible, so you can charge a higher price. What will be the radius of the base of your cones? What will be the height? The discussion: Ms. Longhart asked the students what materials might be useful in helping them solve the problem. Some students suggested making models out of paper circles, while others thought that writing equations and using graphing calculators to find the maximum volume would be best. After some discussion of the relative merits of each approach, Ms. Longhart suggested that they do both and compare their answers. Solving the problem: The students separated into groups to work on the problem. Most students remembered that the volume of a cone is 1/3 pi r2h. They made a variety of paper cones out of circles with radius 10cm, and measured the radius and height of those cones. Using the formula, and a calculator, they generated a table of values, trying to find the maximum volume. They wanted to graph the formula using their calculator, but realized that they needed to solve for h in terms of r. After some initial difficulties, they decided that, since the original circles had a radius of 10 cm, the height of the resulting cone must be SQRT (100 - r2). Then they graphed the equation they had generated on the graphing calculator and used the graph to find the maximum volume. Finally, each group summarized its findings in writing. Summary: Each group listed its actual measurements and its results generated on the graphing calculator on the board and then explained any discrepancies that might have occurred. The class as a whole discussed the accuracy of the solutions. One of the students noticed that, in the cone of maximum volume, the radius was much larger than the height of the cone, and asked why that happened. Ms. Longhart asked the class to think about some possible reasons. To summarize the lesson, Ms. Longhart asked the students to list in their journals all of the mathematical concepts that they used to solve the problem in class that day. For homework, she asked the students to (1) describe how the function they generated would change if the radius of the circle was 8 cm, 9 cm, 11 cm, or 12 cm; (2) find the maximum volumes and corresponding radius for each of the new functions; and (3) determine whether there is a relationship between the radius and the maximum volume for each of the five functions. The First Four Standards - Grades 9-12Vignette - Building ParabolasStandards: In addition to the First Four Standards, this vignette highlights Standards 7 (Geometry), 11 (Patterns), and 13 (Algebra). The problem: Before this session, students in Mr. Evans' class investigated different situations that can be modeled using quadratic functions. They looked at how to maximize the area of a yard given a fixed amount of fencing, and how to predict the path of a rocket. They graphed many quadratic functions, some by plotting points and some on the graphing calculator, and discovered that all of the quadratic functions have graphs that are parabolas. For this session, they went to the computer lab to investigate the relationship of each of the constants in the general form of the parabola to the graph of that equation. The discussion: Before beginning work on the computers, the students reviewed the general shape of a parabola and discussed the differences between one quadratic function and another: the width of the parabola, how high up or down the vertex is, and whether the parabola opens up or down. Mr. Evans introduced the general form of the equation of a parabola, y = a (x - h)2 + k , and asked the students to predict how each of a, h, and k will affect the graph of the parabola. He asked them to explain their reasoning and record their predictions individually in their notebooks, and then he led a discussion of their predictions. Solving the problem: Each pair of students used a program on Green Globs software to predict the equation for a series of parabolas, keeping notes on how the different constants seemed to affect the graphs. There was considerable excitement in the room, as well as some disagreements and some frustration at times. Some pairs of students found that several of the graphs required many attempts before the correct equation was found. At the conclusion of the computer activity, the students compared their results to their predictions and discussed their findings with each other in pairs. They then individually wrote a description of how the values of a, h, and k in the general equation y = a (x - h)2 + k affect the graph of y = x2. Summary: For homework, Mr. Evans asked the students to use their findings to sketch the graphs of several parabolas without using graphing calculators and then to check their sketches by using graphing calculators. He suggested that they revise their journal entries if they find that some of their hypotheses don't work. Mr. Evans began class the next day by having pairs of students play the computer game Green Globs, allowing the students to use only parabolas to hit the globs on the coordinate grid. After about 15 minutes, he led a discussion of the students' findings about parabolas, asking them how they arrived at their hypotheses, what steps they took to verify them, and whether they modified their hypotheses based on their experiences with the homework and the computer game. He then asked the students to think of other areas of mathematics that seem to be related, making connections between their findings about parabolas and what they learned last year about geometric transformations. The First Four Standards - Grades 9-12IndicatorsThe cumulative progress indicators for grade 12 for each of the First Four Standards appear in boldface type below the standard. Each indicator is followed by a brief discussion of how the preceding grade level vignettes might address the indicator in the classroom in grades 9-12. The Introduction to this Framework contains three vignettes describing lessons for grades 9-12 which also illustrate the indicators for the First Four Standards; these are entitled On the Boardwalk, A Sure Thing!?, and Breaking the Mold.
Building upon knowledge and skills gained in the preceding grades, experiences in grades 9-12 will be such that all students: 4*. Pose, explore, and solve a variety of problems, including non-routine problems and open-ended problems with several solutions and/or solution strategies.
5*. Construct, explain, justify, and apply a variety of problem-solving strategies in both cooperative and independent learning environments.
6*. Verify the correctness and reasonableness of results and interpret them in the context of the problems being solved.
7*. Know when to select and how to use grade-appropriate mathematical tools and methods (including manipulatives, calculators and computers, as well as mental math and paper-and-pencil techniques) as a natural and routine part of the problem-solving process.
8*. Determine, collect, organize, and analyze data needed to solve problems.
12*. Construct and use concrete, pictorial, symbolic, and graphical models to represent problem situations and effectively apply processes of mathematical modeling in mathematics and other areas.
14*. Persevere in developing alternative problem-solving strategies if initially selected approaches do not work.
15. Use discovery-oriented, inquiry-based, and problem-centered approaches to investigate and understand the mathematical content appropriate to the high-school grades.
16. Recognize, formulate, and solve problems arising from mathematical situations, everyday experiences, applications to other disciplines, and career applications.
17. Monitor their own progress toward problem solutions.
18. Explore the validity and efficiency of various problem-posing and problem-solving strategies, and develop alternative strategies and generalizations as needed.
Building upon knowledge and skills gained in the preceding grades, experiences in grades 9-12 will be such that all students: 1*. Discuss, listen, represent, read, and write as vital activities in their learning and use of mathematics.
2*. Identify and explain key mathematical concepts, and model situations using oral, written, concrete, pictorial, and graphical methods.
3*. Represent and communicate mathematical ideas through use of learning tools such as calculators, computers, and manipulatives.
4*. Engage in mathematical brainstorming and discussions by asking questions, making conjectures, and suggesting strategies for solving problems.
5*. Explain their own mathematical work to others, and justify their reasoning and conclusions.
6*. Identify and explain key mathematical concepts and model situations using geometric and algebraic methods.
7*. Use mathematical language and symbols to represent problem situations, and recognize the economy and power of mathematical symbolism and its role in the development of mathematics.
8*. Analyze, evaluate, and explain mathematical arguments and conclusions presented by others.
9. Formulate questions, conjectures, and generalizations about data, information, and problem situations.
10. Reflect on and clarify their thinking so as to present convincing arguments for their conclusions.
Building upon knowledge and skills gained in the preceding grades, experiences in grades 9-12 will be such that all students: 1*. View mathematics as an integrated whole rather than as a series of disconnected topics and rules.
2*. Relate mathematical procedures to their underlying concepts.
3*. Use models, calculators, and other mathematical tools to demonstrate the connections among various equivalent graphical, concrete, and verbal representations of mathematical concepts.
8*. Recognize and apply unifying concepts and processes which are woven throughout mathematics.
9*. Use the process of mathematical modeling in mathematics and other disciplines, and demonstrate understanding of its methodology, strengths, and limitations.
10*. Apply mathematics in their daily lives and in career-based contexts.
11*. Recognize situations in other disciplines in which mathematical models may be applicable, and apply appropriate models, mathematical reasoning, and problem solving to those situations.
12. Recognize how mathematics responds to the changing needs of society, through the study of the history of mathematics.
Building upon knowledge and skills gained in the preceding grades, experiences in grades 9-12 will be such that all students: 2*. Draw logical conclusions and make generalizations.
5*. Analyze mathematical situations by recognizing and using patterns and relationships.
8*. Follow and construct logical arguments, and judge their validity.
9*. Recognize and use deductive and inductive reasoning in all areas of mathematics.
10*. Utilize mathematical reasoning skills in other disciplines and in their lives.
11*. Use reasoning rather than relying on an answer-key to check the correctness of solutions to problems.
12. Make conjectures based on observation and information, and test mathematical conjectures, arguments, and proofs.
13. Formulate counter-examples to disprove an argument.
* Adapted from Longhart, Karen. "Making Connections." Eightysomething! Volume 3, Number 2, Summer 1994. * Reference is made here to Indicators 4, 5, 6, 7, 8, 12, and 14, which are also listed for grade 8, since the Standards specify that students demonstrate continued progress in these indicators. * Reference is made here to Indicators 1, 2, 3, 4, 5, 6, 7, and 8, which are also listed for grade 8, since the Standards specify that students demonstrate continued progress in these indicators. * Reference is made here to Indicators 1, 2, 3, 8, 9, 10, and 11, which are also listed for grade 8, since the Standards specify that students demonstrate continued progress in these indicators. * Reference is made here to Indicators 2, 5, 8, 9, 10, and 11, which are also listed for grade 8, since the Standards specify that students demonstrate continued progress in these indicators. |
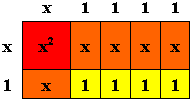 The problem: Yesterday, Mrs. Ellis' class finished a
unit in which they used algebra tiles to help them develop procedures
for multiplying binomials. Today, Mrs. Ellis began by asking the
students to consider the following problem: Suppose we have a
collection of red x2 tiles, orange x
tiles, and yellow unit tiles. Can we put them together to form
a rectangle? For example, if we have one red tile, five orange
tiles, and four yellow tiles, we can make the rectangle at the
right. What combinations of tiles can form a rectangle, and
what combination cannot?
The problem: Yesterday, Mrs. Ellis' class finished a
unit in which they used algebra tiles to help them develop procedures
for multiplying binomials. Today, Mrs. Ellis began by asking the
students to consider the following problem: Suppose we have a
collection of red x2 tiles, orange x
tiles, and yellow unit tiles. Can we put them together to form
a rectangle? For example, if we have one red tile, five orange
tiles, and four yellow tiles, we can make the rectangle at the
right. What combinations of tiles can form a rectangle, and
what combination cannot?