THE FIRST FOUR STANDARDSThe First Four Standards - Grades K-2
OverviewYoung children enter school with informal strategies for solving mathematical problems, communication skills, ideas about how number and shape connect to each other and to their world, and reasoning skills. In grades K-2, students should build upon these informal strategies. Early instruction in problem solving should focus on taking time to understand the problem before rushing to solve it. Kindergartners should begin, for example, by representing problems using physical objects. By second grade, students should begin to move away from dependence on physical objects towards the use of pictures and figures. One of the goals of problem solving in numerical situations is to move students toward the use of more efficient problem solving strategies - from modeling with concrete objects to counting methods to using number facts. Even kindergartners should have experience with multiple-step problems (Mary has 3 cookies. She eats one. Her mother gives her two more. How many cookies does she have now?) in order to focus their attention on understanding the problem and developing a plan for its solution. Students should be able to describe how they have solved a problem and justify their answer. They should also develop the habit of comparing problems to each other, noting how they are alike and different. Communication activities in grades K-2, whether with individuals, small groups, or the whole class, initially emphasize oral (e.g., counting) and pictorial representations. Much time is spent, however, in introducing students to symbolic representations (e.g., numerals and symbols for operations). As students develop written communication skills, they also begin to communicate in writing about mathematics. At first, the teacher may write the students' responses on the board or on sentence strips in order to facilitate this written communication. Students use many concrete representations (e.g., base ten blocks, pattern blocks) and need to learn how to represent their work with these manipulatives through pictures. Students also begin to communicate mathematics using graphs and diagrams. Many mathematical connections begin to be established in kindergarten. Students should connect thenumber three to triangles, for example, as well as to sets of three objects and the numeral 3. Especially important are quantification (how much? how many?), patterns, and representing quantities and shapes. Using children's literature to motivate and set a context for problem solving and learning mathematics is especially appropriate for K-2, as is illustrated in one of the following vignettes. Connections to social studies may involve using graphs to describe characteristics of the class, the school, or the community. Many connections between science and mathematics can be established, from looking for patterns to developing specific skills in measurement and data collection. Children observe life cycles and cycles in nature, such as the seasons, and the growth and decay of plant forms. Children begin by using words to describe physical characteristics: color intensity (bright or dull), sound volume (loud or quiet), temperature (hot or cold), and size (longest or shortest). This allows them to make simple descriptive comparisons and to place objects in an order. They move on to using numbers to describe such characteristics. For example, students might measure the height of plants at different times, summarize their data in a table, and prepare a graph (bar or line) showing the height over time. They might repeat the experiment with different growing conditions, and then compare their graphs for the different conditions. Students in grades K-2 should spend a great deal of time on inductive reasoning, looking for patterns, making educated guesses, generating hypotheses, and forming generalizations based on their experiences. They should also begin to develop some skill in drawing logical conclusions and justifying answers (deductive reasoning), perhaps by using manipulatives such as attribute blocks. They should continually strive to make sense of mathematics by using reasoning to predict answers and compare and contrast examples and problem situations. In grades K-2, students build on what they already know as they develop their skills in problem solving, communication, mathematical connections, and reasoning. They begin to move from informal, intuitive strategies and processes towards more symbolic representations and more explicit recognition of their thinking strategies. On-Line Resources
The First Four Standards - Grades K-2Vignette - Will a Dinosaur Fit?Standards: In addition to the First Four Standards, this vignette highlights Standards 6 (Number Sense), 7 (Geometry), 9 (Measurement), and 11 (Estimation). The problem: The second grade was in the midst of a unit on dinosaurs when the teacher read to her class the book Danny and the Dinosaur by Syd Hoff (Harper & Row, 1958). After the first reading, the children re-examined some of the illustrations. One picture depicted the dinosaur larger than a block of homes, another showed the dinosaur almost completely hidden by one house. One picture showed the dinosaur taller than an apartment building and yet another showed the dinosaur not quite as tall as a lamp post. Students were intrigued by the idea that Danny's dinosaur friend did not seem to be of a consistent size. They voiced opinions about the dinosaur's actual size. Since students seemed to have a sustained interest in exploring the sizes of dinosaurs, the teacher presented students with this question: Do you think that a dinosaur could fit into our classroom? The discussion: Brainstorming was encouraged by the teacher as questions such as the following were posed by students and by the teacher. What does it mean to "fit" in the classroom? What information would we need to get in order to determine if a dinosaur could fit in our classroom? Do you think all of our answers will be the same? Why? What do we know already that might help us? What materials do you think we would need? Solving the problem: Students worked in groups of 3 over a period of several days. They began by choosing a specific dinosaur and then they used a variety of books and computer software in the classroom to find the size of their dinosaur. They determined the size of the classroom, choosing to measure with a trundle wheel or a tape, or by using estimation. Then they decided, by comparing the measures found in books with those made of the classroom, whether the dinosaur would fit into the classroom. Each group was responsible for creating a display and making a presentation to the class to answer the question. The displays made use of models, pictures, and text. Students with more than a few sentences to write were encouraged to make use of the word processor available in the classroom. Summary: Students used their displays to make presentations to the class. There were a variety of answers. Those who had chosen one of the smaller dinosaurs, the velociraptors, for example, found that the dinosaur could walk through the doorway and several dinosaurs would fit in the room. Others, who had chosen larger dinosaurs, the stegosaurus, for example, found that if the dinosaur could have gotten through the doorway, several would have fit in the room. Still others, who had chosen very large dinosaurs, the brachiosaurus, for example, found that the dinosaur would not have fit into the room at all. As the presentations ended, several children suggested further explorations that might be interesting: Would the dinosaur I chose fit into the multi-purpose room? Was the dinosaur I chose as long as the driveway in front of the school? Was the dinosaur I chose taller than the school building? The First Four Standards - Grades K-2Vignette - ShapetownStandards: In addition to the First Four Standards, this vignette highlights Standards 7 (Geometry), 11 (Patterns), and 14 (Discrete Mathematics). The problem: The students in kindergarten had been involved in a unit that allowed them to explore their town. They had been exposed to a variety of activities, including building symmetric and non-symmetric block buildings, drawing neighborhood maps, and using letter-number ordered pairs (like A-2) to locate places on a grid. In this lesson, pairs of students were challenged to build towns with attribute blocks and loops based on a rule or pattern that they made up. The discussion: With the class sitting on the carpet in a circle, the teacher placed a loop within everyone's sight. She explained that the loop was a town and that the blocks were buildings. Using blocks of different colors, she then placed several triangles inside the loop and several non-triangles outside the loop. Ideas about the rule used to build Town 1 were discussed: Tell me about the town. Describe a pattern that you see. Put this triangle on the carpet to follow the pattern. Put this circle on the carpet to follow the pattern. How could you tell someone else about our town so they could build one just like it? The verbalization was then called the rule for the town. Town 2 was created with two loops, blocks were placed inside and outside these loops, and similar questions were raised and discussed. Several reasonable rules were suggested. For example, one rule was: triangles in one loop, blue blocks in the other loop, other colors and shapes in the overlapping loop and outside the loop. Another rule was: triangles in one loop, blue blocks in the other loop, blue triangles in the overlapping loop, and all other blocks outside the loops. 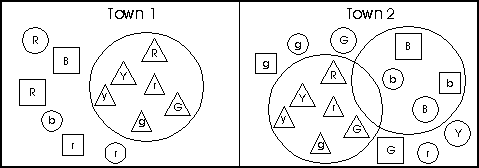
Solving the problem: Students were given loops and some attribute blocks. They were challenged to work together to build a town that used a rule. At the end of the working time, each pair of students challenged the class to place other blocks in their town and then to verbalize the rule that was used to create the town. Summary: Students worked independently to record their town designs using crayons and shapes cut from colored construction paper. Students described the rules that they used to build their towns. The First Four Standards - Grades K-2IndicatorsThe cumulative progress indicators for grade 4 for each of the First Four Standards appear in boldface type below the standard. Each indicator is followed by a brief discussion of how the preceding grade-level vignettes might address the indicator in the classroom in kindergarten and in grades 1 and 2. The Introduction to this Framework contains three vignettes describing lessons for grades K-4 which also illustrate the indicators for the First Four Standards; these are entitled Elevens Alive!, Product and Process, and Sharing a Snack.
Experiences will be such that all students in grades K-2: 1. Use discovery-oriented, inquiry-based, and problem-centered approaches to investigate and understand mathematical content appropriate to the early elementary grades.
2. Recognize, formulate, and solve problems arising from mathematical situations and everyday experiences.
3. Construct and use concrete, pictorial, symbolic, and graphical models to represent problem situations.
4. Pose, explore, and solve a variety of problems, including non-routine problems and open-ended problems with several solutions and/or solution strategies.
5. Construct, explain, justify, and apply a variety of problem-solving strategies in both cooperative and independent learning environments.
6. Verify the correctness and reasonableness of results and interpret them in the context of the problems being solved.
7. Know when to select and how to use grade-appropriate mathematical tools and methods (including manipulatives, calculators and computers, as well as mental math and paper-and-pencil techniques) as a natural and routine part of the problem-solving process.
8. Determine, collect, organize, and analyze data needed to solve problems.
9. Recognize that there may be multiple ways to solve a problem.
Experiences will be such that all student in grades K-2: 1. Discuss, listen, represent, read, and write as vital activities in their learning and use of mathematics.
2. Identify and explain key mathematical concepts, and model situations using oral, written, concrete, pictorial, and graphical methods.
3. Represent and communicate mathematical ideas through the use of learning tools such as calculators, computers, and manipulatives.
4. Engage in mathematical brainstorming and discussions by asking questions, making conjectures, and suggesting strategies for solving problems.
5. Explain their own mathematical work to others, and justify their reasoning and conclusions.
Experiences will be such that all students in grades K-2: 1. View mathematics as an integrated whole rather than as a series of disconnected topics and rules.
2. Relate mathematical procedures to their underlying concepts.
3. Use models, calculators, and other mathematical tools to demonstrate the connections among various equivalent graphical, concrete, and verbal representations of mathematical concepts.
4. Explore problems and describe and confirm results using various representations.
5. Use one mathematical idea to extend understanding of another.
6. Recognize the connections between mathematics and other disciplines, and apply mathematical thinking and problem solving in those areas.
7. Recognize the role of mathematics in their daily lives and in society.
Experiences will be such that all students in grades K-2: 1. Make educated guesses and test them for correctness.
2. Draw logical conclusions and make generalizations.
3. Use models, known facts, properties, and relationships to explain their thinking.
4. Justify answers and solution processes in a variety of problems.
5. Analyze mathematical situations by recognizing and using patterns and relationships.
|