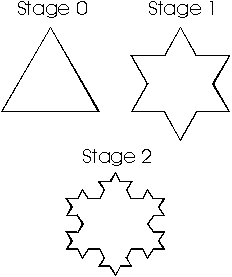STANDARD 7 - GEOMETRY AND SPATIAL SENSE
K-12 Overview
|
All students will develop spatial sense and an ability to use
geometric properties and relationships to solve problems in
mathematics and in everyday life.
|
Descriptive Statement
Spatial sense is an intuitive feel for shape and space. It
involves the concepts of traditional geometry, including an ability to
recognize, visualize, represent, and transform geometric shapes. It
also involves other, less formal ways of looking at two- and
three-dimensional space, such as paper-folding, transformations,
tessellations, and projections. Geometry is all around us in art,
nature, and the things we make. Students of geometry can apply their
spatial sense and knowledge of the properties of shapes and space to
the real world.
Meaning and Importance
Geometry is the study of spatial relationships. It is connected to
every strand in the mathematics curriculum and to a multitude of
situations in real life. Geometric figures and relationships have
played an important role in society's sense of what is
aesthetically pleasing. From the Greek discovery and architectural
use of the golden ratio to M. C. Escher's use of tessellations to
produce some of the world's most recognizable works of art,
geometry and the visual arts have had strong connections.
Well-constructed diagrams allow us to apply knowledge of geometry,
geometric reasoning, and intuition to arithmetic and algebra problems.
The use of a rectangular array to model the multiplication of two
quantities, for instance, has long been known as an effective strategy
to aid in the visualization of the operation of multiplication. Other
mathematical concepts which run very deeply through modern mathematics
and technology, such as symmetry, are most easily introduced in a
geometric context. Whether one is designing an electronic circuit
board, a building, a dress, an airport, a bookshelf, or a newspaper
page, an understanding of geometric principles is required.
K-12 Development and Emphases
Traditionally, elementary school geometry instruction has focused
on the categorization of shapes; at the secondary level, it has been
taught as the prime example of a formal deductive system. While these
perspectives of the content are important, they are also limiting. In
order to develop spatial sense, students should be exposed to a
broader range of geometric activities at all grade levels.
By virtue of living in a three-dimensional world, having dealt with
space for five years, children enter school with a remarkable amount
of intuitive geometric knowledge. The geometry curriculum should take
advantage of this intuition while expanding and formalizing the
students' knowledge. In early elementary school, a rich,
qualitative, hands-on study of geometric objects helps young children
develop spatial sense and a strong intuitive grasp of geometric
properties and relationships. Eventually they develop a comfortable
vocabularyof appropriate geometric terminology. In the middle school
years, students should begin to use their knowledge in a more
analytical manner to solve problems, make conjectures, and look for
patterns and generalizations. Gradually they develop the ability to
make inferences and logical deductions based on geometric
relationships and to use spatial intuition to develop more generic
mathematical problem-solving skills. In high school, the study of
geometry expands to address coordinate, vector, and transformational
viewpoints which utilize both inductive and deductive reasoning.
Geometry instruction at the high school level should not be limited to
formal deductive proof and simple measurement activities, but should
include the study of geometric transformations, analytic geometry,
topology, and connections of geometry with algebra and other areas of
mathematics.
At all grade levels, the study of geometry should make abundant use
of experiences that require active student involvement. Constructing
models, folding paper cutouts, using mirrors, pattern blocks,
geoboards, and tangrams, and creating geometric computer graphics all
provide opportunities for students to learn by doing, to reflect upon
their actions, and to communicate their observations and conclusions.
These activities and others of the same type should be used to achieve
the goals in the seven specific areas of study that constitute this
standard and which are described below.
In their study of spatial relationships, young students
should make regular use of concrete materials in hands-on activities
designed to develop their understanding of objects in space. The
early focus should be the description of the location and orientation
of objects in relation to other objects. Additionally, students can
begin an exploration of symmetry, congruence, and similarity. Older
students should study the two-dimensional representations of
three-dimensional objects by sketching shadows, projections, and
perspectives.
In the study of properties of geometric figures, students
deal explicitly with the identification and classification of standard
geometric objects by the number of edges and vertices, the number and
shapes of the faces, the acuteness of the angles, and so on.
Cut-and-paste constructions of paper models, combining shapes to form
new shapes and decomposing complex shapes into simpler ones are useful
exercises to aid in exploring shapes and their properties. As their
studies continue, older students should be able to understand and
perform classic constructions with straight edges and compasses as
well as with appropriate computer software. Formulating good
mathematical definitions for geometric shapes should eventually lead
to the ability to make hypotheses concerning relationships and to use
deductive arguments to show that the relationships exist.
The standard geometric transformations include translation,
rotation, reflection, and scaling. They are central to the study of
geometry and its applications in that these movements offer the most
natural approach to understanding congruence, similarity, symmetry,
and other geometric relationships. Younger children should have a
great deal of experience with flips, slides, and turns
of concrete objects, figures made on geoboards, and drawn figures.
Older students should be able to use more formal terminology and
procedures for determining the results of the standard
transformations. An added benefit of experience gained with simple
and composite transformations is the mathematical connection that
older students can make to functions and function composition.
Coordinate geometry provides an important connection between
geometry and algebra. Students can work informally with coordinates
in the primary grades by finding locations in the room, and by
studying simple maps of the school and neighborhood. In later
elementary grades, they can learn to plot figures on a coordinate
plane, and still later, study the effects of various transformations
on the coordinates of the points of two- and three-dimensional
figures. High-school students should be able to represent
geometrictransformations algebraically and interpret algebraic
equations geometrically.
Measurement and geometry are interrelated, and an understanding of
the geometry of measurement is necessary for the understanding
of measurement. In elementary school, students should learn the
meaning of such geometric measures as length, area, volume and angle
measure and should be actively involved in the measurement of those
attributes for all kinds of two- and three-dimensional objects, not
simply the standard ones. Throughout school, they should use
measurement activities to reinforce their understanding of geometric
properties. All students should use these experiences to help them
understand such principles as the quadratic change in area and cubic
change in volume that occurs with a linear change of scale.
Trigonometry and its use in making indirect measurements provides
students with another view of the interrelationships between geometry
and measurement.
Geometric modeling is a powerful problem-solving skill and
should be used frequently by both teachers and students. A simple
diagram, such as a pie-shaped graph, a force diagram in physics, or a
dot-and-line illustration of a network, can illuminate the essence of
a problem and allow geometric intuition to aid in the approach to a
solution. Visualization skills and understanding of concepts will
both improve as students are encouraged to make such models.
The relationship between geometry and deductive reasoning
originated with the ancient Greek philosophers, and remains an
important part of the study of geometry. A key ingredient of
deductive reasoning is being able to recognize which statements have
been justified and which have been assumed without proof. This is an
ability which all students should develop in all areas, not just
geometry, or even just mathematics! At first, deductive reasoning is
informal, with students inferring new properties or relationships from
those already established, without detailed explanations at every
step. Later, deduction becomes more formal as students learn to use
all permissible assumptions in a proof and as all statements are
systematically justified from what has been assumed or proved before.
The idea of deductive proof should not be confused with the specific
two-column format of proof found in most geometry textbooks. The
reason for studying deductive proof is to develop reasoning skills,
not to write out arguments in a particular arrangement. Note that
proof by mathematical induction is another deductive method that
should not be neglected.
Much of the current thinking about the development of geometric
thinking in students comes from the work of a pair of Dutch
researchers, Pierre van Hiele and Dina van Hiele-Geldof. Their model
of geometric thinking identifies five levels of development through
which students pass when assisted by appropriate instruction.
- Visual recognition of shapes by their appearances
as a whole (level 0)
- Analysis and description of shapes in terms of
their properties (level 1)
- Higher "theoretical" levels involving
informal deduction (level 2)
- Formal deduction involving axioms and theorems
(level 3)
- Work with abstract geometric systems (level 4).
(Geddes & Fortunato, 1993)
Although the levels are not completely separate and the transitions
are complex, the model is very useful for characterizing levels of
students' thinking. Consistently, the research shows that
appropriately targeted instruction is critical to children's
movement through these levels. Stagnation at early levels is the
frequent result of a geometry curriculum that never moves beyond
identification of shapes and their properties. The discussion in this
K-12 Overview draws on this van-Hiele model of geometric thinking.
In summary, students of all ages should recognize and be
aware of the presence of geometry in nature, in art, and in
human-built structures. They should realize that geometry and
geometric applications are all around them and, through study of those
applications, come to better understand and appreciate the role of
geometry in life. Carpenters use triangles for structural support,
scientists use geometric models of molecules to provide clues to
understanding their chemical and physical properties, and merchants
use traffic-flow diagrams to plan the placement of their stock and
special displays. These and many, many more examples should leave no
doubt in students' minds as to the importance of the study of
geometry.
Note: Although each content
standard is discussed in a separate chapter, it is not the intention
that each be treated separately in the classroom. Indeed, as
noted in the Introduction to this Framework, an effective
curriculum is one that successfully integrates these areas to
present students with rich and meaningful cross-strand
experiences.
Reference
-
Geddes, Dorothy, & Fortunato, Irene. "Geometry:
Research and Classroom Activities," in D. T. Owens, Ed.,
Research Ideas for the Classroom: Middle Grades Mathematics.
New York: Macmillan, 1993.
Standard 7 - Geometry and Spatial Sense - Grades K-2
Overview
Students can develop strong spatial sense from consistent
experiences in classroom activities that use a variety of
manipulatives and technology. The key components of spatial sense, as
identified in the K-12 Overview, are spatial relationships, properties
of geometric figures, geometric transformations, coordinate geometry,
geometry of measurement, geometric modeling, and reasoning.
In kindergarten through second grade, the emphasis is on
qualitative, not quantitative, properties of geometric objects.
Students are at the visualization level of geometric thinking, where
they perceive figures as "wholes". They recognize squares
and rectangles, but perhaps not that squares are a special case of
rectangles. To enrich and develop their geometric thinking, children
at these grade levels need to explore geometry using a variety of
physical objects, drawings, and computer tools. They work with
solids, pattern blocks, templates, geoboards, and computer drawing
tools to develop their understanding of geometric concepts and their
spatial sense. They construct models and drawings to experiment with
orientation, position, and scale, and to develop visualization skills.
Students begin to develop a geometric vocabulary. A sample unit on
geometry for the second-grade level can be found in Chapter 17 of this
Framework.
In their study of spatial relationships, students focus on
developing their understanding of objects in space. They discuss and
describe the relative positions of objects using phrases like "in
front of" and "on top of." They describe and draw
three-dimensional objects in different relative locations. They
compare and contrast shapes, describing the shapes of the faces and
bases of three-dimensional figures. They discuss symmetry and look
for examples of symmetry in their environment. They look for shapes
that are the same size and shape (congruent) or the same shape but
different sizes (similar). They use mirrors to explore symmetry.
In beginning their study of properties of geometric figures,
students look for shapes in the environment, make models from sticks
and clay or paper and glue, and draw shapes. They sort objects
according to shape. They recognize, classify, sort, describe, and
compare geometric shapes such as the sphere, cylinder, cone,
rectangular solid, cube, square, circle, triangle, rectangle,
hexagon, trapezoid, and rhombus. They describe the angle at which two
edges meet in different polygons as being smaller than a right angle,
a right angle, or larger than a right angle. They discuss points,
lines, line segments, intersecting and non-intersecting lines, and
midpoints of lines.
Students begin looking at geometric transformations by using
concrete materials such as paper dolls to model slides (translations),
flips (reflections), and turns (rotations). Students put shapes
together to make new shapes and take shapes apart to form simpler
shapes. Students work on spatial puzzles, often involving pattern
blocks or tangrams. They look for plane shapes in complex drawings
and explore tilings. They divide figures into equal fractional parts,
for example, by folding along one, two, or three lines.
Coordinate geometry in grades K-2 involves describing the
motion of an object. Students make maps of real, imaginary, or
storybook journeys. They describe the location of an object on a grid
or a point in aplane using numbers or letters. They give instructions
to an imaginary "turtle" to crawl around the outline of a
figure.
Students in these grades also begin to explore the geometry of
measurement. In kindergarten, students discuss and describe
quantitative properties of objects using phrases like
"bigger" or "longer." They order objects by
length or weight. In first and second grade, they quantify properties
of objects by counting and measuring. They determine the areas of
figures by cutting them out of grid paper and counting the squares.
They measure the perimeter of a polygon by adding the lengths of all
of the sides.
Students begin to explore geometric modeling by constructing
shapes from a variety of materials, including toothpicks and clay,
paper and glue, or commercial materials. They use templates to draw
designs, and record what they have constructed out of pattern blocks
and tangrams. They fold, draw, and color shapes. They copy geoboard
figures, and construct them both from memory and by following oral or
written instructions. They may also use geometric models, such as the
number line, for skip counting or repeated addition.
Geometry provides a rich context in which to begin to develop
students' reasoning skills. Students apply thinking
skills in geometric tasks from identifying shapes to discovering
properties of shapes, creating geometric patterns, and solving
geometric puzzles and problems in a variety of ways. They create,
describe, and extend geometric patterns. They use attribute blocks to
focus on the similarities and differences of objects.
Geometry provides a unique opportunity to focus on the First Four
Standards, especially Standard 2 which stresses the importance of
making connections to other mathematical topics. For example,
students often use their understanding of familiar shapes to help
build an understanding of fractions. Teachers in grades K-2 need to
plan classroom activities that involve several mathematical processes
and relate geometry to other topics in mathematics. Geometry should
not be taught in isolation; it should be a natural and integrated part
of the entire curriculum.
Standard 7 - Geometry and Spatial Sense - K-2
Indicators and Activities
The cumulative progress indicators for grade 4 appear below in
boldface type. Each indicator is followed by activities which
illustrate how it can be addressed in the classroom in kindergarten
and grades 1 and 2.
Experiences will be such that all students in grades K-2:
1. Explore spatial relationships such as the
direction, orientation, and perspectives of objects in space,
their relative shapes and sizes, and the relations between objects and
their shadows or projections.
- Blindfolded students are given real objects to
touch and then, with the blindfolds removed, select the objects from a
collection of visible objects.
- Students work through the Will a Dinosaurs
Fit? lesson that is described in the First Four Standards of this
Framework. They discuss the size of the different dinosaurs
and arrange them from smallest to largest.
- Students predict what shape will result when a
small piece is cut out of a folded piece of paper in different ways
(along a diagonal, across a fold or a corner, or in the center) and
the paper is then unfolded.
- Students compare the sequence of objects seen
from different points of view. For example, from the classroom
window, the swings are to the left of the monkeybars, but the
relationship is reversed if the objects are viewed from the blacktop
facing the classroom.
- Students predict and draw what the shadow of an
object placed between a light and a screen will look
like.
2. Explore relationships among shapes, such as
congruence, symmetry, similarity, and self-similarity.
- Students look for examples of congruent figures
(same size and shape) in the environment.
- Students explore symmetry by using mirrors with
pattern blocks or by folding paper or by making inkblot designs.
Students find the lines of symmetry in the letters of the alphabet and
in numerals. They fold paper and cut out symmetric designs. They
identify the symmetry in wallpaper or giftwrap designs.
- Students use different size dolls and action
figures as an introduction to the concept of similarity (same shape,
different size).
3. Explore properties of three- and
two-dimensional shapes using concrete objects, drawings, and
computer graphics.
- Students predict what shape they will see when
they make various impressions of 3-dimensional objects in sand. For
example, the top of a cylinder forms a circle, its side formsa
rectangle.
- Students outline a triangle, a square, and a
circle on the floor with string or tape. Then they walk around each
figure, chanting a rhyme, such as "Triangle, triangle, triangle,
1, 2,3, I can walk around you as easy as can be," and counting
the sides as they walk.
- Students work through the Shapetown
lesson that is described in the First Four Standards of this
Framework. They explore properties of two-dimensional shapes
by applying the fundamental concepts of Venn diagrams.
- Some students use
MuppetTM Math to work with
Kermit's geometric paintings, while others use Shape Up!
to compare everyday objects to geometric shapes.
4. Use properties of three- and two-dimensional
shapes to identify, classify, and describe shapes.
- Students make shapes with their fingers and arms.
- Students listen to and look at the book The
Shapes Game by Paul Rogers. Each page shows a different shape and
many of the things in the world that have that shape. As each page is
read, the children find other objects in the room that have the same
shape.
- Students listen to and draw illustrations for
the story The Greedy Triangle by Marilyn Burns.
- A good open-ended assessment for this critical
indicator is to ask students to sort a collection of shapes into
groups, explaining their reasoning. Some groups they might consider
include "all right angles" or "four-siders." The
teacher should encourage the students to invent appropriate group
names and to use informal language to describe the properties, and
should record the students' responses to look for progress over
time.
- A more traditional, but still useful, assessment
strategy is to ask students to sort pictures cut from magazines
according to shape. This more focused task will generate information
about the students' ability to recognize and differentiate among
shapes.
- Students make class books shaped like a
triangle, a rectangle, a square, and a circle. They fill each book
with pictures of objects that have the shape of the
book.
- Students turn a geometric shape into a picture.
For example, a triangle might become a tower, a clown face, or the
roof of a house.
5. Investigate and predict the results of
combining, subdividing, and changing shapes.
- Students use tangram pieces
to construct triangles, rectangles, squares, and other
shapes.
- Students investigate which pattern block shapes
can be formed from the equilateral triangles, recording their results
in pictures and on a chart.
- Students work in groups to decide how to divide
a rectangular candy bar among four people. The students then compare
the various ways that each group solved the problem.
6. Use tessellations to explore properties of
geometric shapes and their relationships to the concepts of
area and perimeter.
- Students use Unifix cubes
or pattern blocks to create colorful designs. They then discusshow
many blocks they used (area) and the distance around their design
(perimeter). They also discuss why these polygon shapes fit together
like a puzzle.
- Students use different shapes to make quilt
patterns.
- During free play time, students use pattern
blocks to make different space-filling designs. They record any
patterns that they especially like, using templates or drawing around
the blocks.
7. Explore geometric transformations such as
rotations (turns), reflections (flips), and translations
(slides).
- Students look at the world
around them for examples of changes in position that do not change
size or shape. For example, a child going down a slide illustrates a
slide, a merry-go-round or hands on a clock illustrate a turn, and a
mirror illustrates a flip.
- Students look through and discuss the no-text
book Changes, Changes by Pat Hutchins. In it, a man and a
woman use the same set of building blocks to transform a house into a
fire engine, then a boat, a truck, and back to a house. The students
tell the story and then draw pictures to show how the blocks changed
from one object to another.
- Students investigate the shapes that they can
see when they place a mirror on a square pattern block.
8. Develop the concepts of coordinates and paths,
using maps, tables, and grids.
- Students use maps of their
community to find various ways to get from school to the park. They
use letters and numbers to describe the location of the school and
that of the park.
- Students create a map based on the familiar
story of The Little Gingerbread Man, showing where each of the
people in the story lives.
- Students describe how to get from one point in
the school to another and try to follow each others'
directions.
9. Understand the variety of ways in which
geometric shapes and objects can be measured.
- In connection with a unit
on dinosaurs in science, students discuss the different ways in which
the size of dinosaurs can be described. They decide to measure the
size of a dinosaur's footprint in two ways: by using string to
measure the distance around it and by using base ten blocks to measure
the space inside it.
- Pairs of students investigate the many different
designs that they can make using unit squares and 1/2-unit right
triangles. They record their results on dot paper.
10. Investigate the occurrence of geometry in nature,
art, and other areas.
- Students take a "geometry walk"
through their school or their neighborhood, looking for examples of
specific shapes and concepts.
- Students create geometric patterns using potato
prints.
- Students decorate their classroom for the winter
holidays using geometric shapes.
- Students examine and discuss geometric patterns
found in works of art.
References
-
Burns, Marilyn. The Greedy Triangle. New York:
Scholastic, Inc., 1994.
Hutchins, Pat. Changes, Changes. New York: MacMillan,
1987.
Rogers, Paul. The Shapes Game. New York: Henry Holt and
Company, 1989.
Software
-
MuppetTM Math. Jim Henson Productions.
Sunburst Communications.
Shape Up! Sunburst Communications.
General Reference
-
Burton, G. and T. Coburn. Curriculum and Evaluation Standards
for School Mathematics: Addenda
Series: Kindergarten Book. Reston, VA: National Council of
Teachers of Mathematics, 1991.
On-Line Resources
-
http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/
The Framework will be available at this site during
Spring 1997. In time, we hope to post additional resources
relating to this standard, such as grade-specific activities submitted
by New Jersey teachers, and to provide a forum to discuss the
Mathematics Standards.
Standard 7 - Geometry and Spatial Sense - Grades 3-4
Overview
Students can develop strong spatial sense from consistent
experiences in classroom activities that use a wide variety of
manipulatives and technology. The key components of spatial sense, as
identified in the K-12 Overview, are spatial relationships,
properties of geometric figures, geometric transformations, coordinate
geometry, geometry of measurement, geometric modeling, and
reasoning.
In third and fourth grade, students are beginning to move beyond
recognizing whole shapes to analyzing the relevant properties of a
shape. They continue to use their own observations about shapes and
the relations among these shapes in the physical world to build
understanding of geometric concepts. Thus, using manipulative
materials to develop geometric concepts and spatial sense remains
important at these grade levels. Exploring concepts in a number of
different contexts helps students to generalize. Students are
extending their understanding of cause and effect and their ability to
make conjectures. They are particularly interested in Why?
Questions such as Why are most rooms shaped like rectangles?
offer interesting points of departure for studying geometric
concepts. Connections among geometry, spatial sense, other areas of
mathematics, and other subject areas provide many opportunities for
students to see how mathematics fits into their lives.
With respect to spatial relationships, students in these
grade levels continue to examine direction, orientation, and
perspectives of objects in space. They are aware of the relative
positions of objects; you might ask Which walls are opposite each
other? What is between the ceiling and the floor? Students also
expand their understanding of congruence, similarity, and symmetry.
They can identify congruent shapes, draw and identify a line of
symmetry, and describe the symmetries found in nature. They search
for examples in nature where each part of an item looks like a
miniature version of the whole (self-similar).
Students are extending their understanding of properties of
geometric figures. Now they are ready to discuss these more
carefully and to begin relating different figures to each other. By
experimenting with concrete materials, drawings, and computers, they
are able to discover properties of shapes and to make generalizations
like all squares have four equal sides. They use the language
of properties to describe shapes and to explain solutions for
geometric problems, but they are not yet able to deduce new properties
from old ones or consider which properties are necessary and
sufficient for defining a shape. They recognize the concepts of
point, line, line segment, ray, plane, intersecting lines, radius,
diameter, inside, outside, and on a figure. They extend the shapes
they can identify to include ellipses, pentagons, octagons, cubes,
cylinders, cones, prisms, pyramids, and spheres.
Students continue to explore geometric transformations.
Using concrete materials, pictures, and computer graphics, they
explore the effects of transformations on shapes.
Using coordinate geometry students create and interpret
maps, sometimes making use of information found in tables and charts.
Some grids use only numbers at these grade levels, while others use a
combination of letters and numbers.
The geometry of measurement begins to take on more
significance in grades 3 and 4, as students focusmore on the concepts
of perimeter and area. Students learn different ways of finding the
perimeter of an object: using string around the edge and then
measuring the length of the string, using a measuring tape, measuring
the length of each side and then adding the measures together, or
using a trundle wheel. They also develop non-formula-based strategies
for finding the area of a figure.
Geometric modeling allows students to approach topics
visually. For example, geometric shapes allow students to build an
understanding of fraction concepts as they cut the shapes into
congruent pieces. They can use the problem solving skill of drawing
geometric diagrams, such as a polygon with its diagonals, to find out
how many matches are played in a round robin tournament. They
continue to build three-dimensional models of shapes, to draw two- and
three-dimensional shapes with increasing accuracy, and to use
computers to help them analyze geometric properties.
Students' use of reasoning continues to provide
opportunities to connect geometry to Standards 1 - 4, to other areas
of mathematics, to other disciplines, and to the real world. Students
explain how they have approached a particular problem, share results
with each other, and justify their answers.
Students in third and fourth grade are still dealing with geometry
in a qualitative way but are beginning to adopt more quantitative
points of view. They are able to use their natural curiosity about
the world to expand their understanding of geometric concepts and
spatial sense.
Standard 7 - Geometry and Spatial Sense - Grades 3-4
Indicators and Activities
The cumulative progress indicators for grade 4 appear below in
boldface type. Each indicator is followed by activities which
illustrate how it can be addressed in the classroom in grades 3 and
4.
Building upon knowledge and skills gained in the preceding grades,
experiences in grades 3-4 will be such that all students:
1. Explore spatial relationships such as the direction,
orientation, and perspectives of objects in space, their
relative shapes and sizes, and the relations between objects and their
shadows or projections.
- Students compare the sizes of the many shapes
found in the classroom, such as the heights of students or the areas
of their hands.
- The teacher holds up a shape or describes a
shape. Students locate this shape hidden in a box or bag containing a
number of shapes, without looking at the shapes.
- Students explore what happens to the shadow of a
square when it is held at various angles to a beam of light. They
continue their investigation with other two- and three-dimensional
figures.
- At half-hour intervals, students measure the
length of the shadow of a stick stuck vertically into the
ground.
- Students trace the faces of a solid on a
transparency and then challenge each other to identify the solid.
They check their guess by bringing the solid to the overhead projector
and placing it on each face in turn.
- Students read Ellipse by Mannis Charosh.
This one-concept book illustrates ellipses in all of their possible
orientations and describes a variety of experiments that the students
can perform to better understand the role of perspective in
geometry.
- Students predict the positions of three students
from different points of view (perspective). For example, from the
front of the room, they might see Joe on the left, Rhonda in the
middle, and Carly on the right. From the back of the room, the
positions would be reversed. Students find a perspective from which
Rhonda is on the left, Carly is in the middle and Joe is on the
right.
2. Explore relationships among shapes, such as
congruence, symmetry, similarity, and self-similarity.
- Students make a collection of natural shapes,
including a wide variety of three-dimensional shapes such as fruits
and vegetables, shells, flowers, and leaves. They describe the
symmetry found in these shapes.
- Students find objects that exhibit
self-similarity, i.e., that contain copies of a basic motif which is
repeated at smaller sizes of the same shape. Examples of such objects
arefeathers, the shape of a coastline, chambered nautilus shells, and
plants which branch out such as cauliflower, broccoli, Queen
Anne's lace, and ferns.
- Students look for examples of congruent figures
(same size and shape) in the environment.
- Students use scale models of cars and airplanes
to study similarity. They recognize that figures that have the same
shape but different sizes are similar.
3. Explore properties of three- and
two-dimensional shapes using concrete objects, drawings, and
computer graphics.
- Students look for a "Shape of the Day"
throughout the school day, recording the number of times that the
shape is seen.
- Students look for lines in the classroom,
identifying pairs of lines that are parallel, that intersect, or that
are perpendicular.
- Students use the computer language Logo to
describe the path made by a turtle as it goes around different
geometric shapes.
4. Use properties of three- and two-dimensional
shapes to identify, classify, and describe shapes.
- Students make a chart or bar graph showing how
many squares, rectangles, triangles, etc., they find in their
classroom.
- Students "walk" a shape and have other
students guess the shape.
- Students classify shapes according to whether
they contain right angles only, all angles smaller than a right angle,
or at least one angle larger than a right angle.
- One student thinks of a shape. The others ask
questions about its properties, trying to guess it. For example,
Does it have a right angle?
5. Investigate and predict the results of
combining, subdividing, and changing shapes.
- Students investigate the shapes found in their
lunches and then discuss how the shapes change as they nibble away.
For example: Can you change a four-sided sandwich into a
triangle?
- Students investigate how to use four triangles
from the pattern blocks to make a large triangle, a four-sided figure,
and a six-sided figure.
- Students combine tangram pieces to create a
variety of shapes.
6. Use tessellations to explore properties of
geometric shapes and their relationships to the concepts of
area and perimeter.
- Students use square, triangular, and hexagonal
grid paper to create colorful designs. They discuss why these polygon
shapes fit together like a puzzle.
- Students use Unifix cubes or pattern blocks to create
designs. They then discuss how many blocks they used (area) and the
distance around their design (perimeter).
- Students work through the Tiling a Floor
lesson that is described in the First FourStandards of this
Framework. They discover that the shapes which can be used for
tiling must be able to fit around a point without leaving spaces and
without overlapping.
7. Explore geometric transformations such as
rotations (turns), reflections (flips), and translations
(slides).
- Students use stuffed animals or two-sided paperdolls to
show movements in the plane: slides, flips, and turns. They discuss
how all slides (or flips or turns) are alike.
- Students create borders from a single simple design element
which is repeated using slides, flips, and turns.
- Students study and describe the use of
transformations in Pennsylvania Dutch hex signs, and then they design
their own.
- Students discuss transformations found in nature, such as
the symmetry in the wings of a butterfly (a flip), the way a honeycomb
is formed (slides of hexagons), or the petals of a flower
(turns).
- Students create quilt designs by using geometric
transformations to repeat a basic pattern.
8. Develop the concepts of coordinates and paths,
using maps, tables, and grids.
- Students create Logo procedures for drawing
rectangles or other geometric figures.
- A good interdisciplinary assessment in both reading and
mathematics is to have students draw maps for stories they have read,
using coordinates to identify the locations of critical events or
objects in the story.
- Students find the lengths of paths on a grid, such as the
distance from Susan's house to school.
9. Understand the variety of ways in which
geometric shapes and objects can be measured.
- Students discuss how to describe the size of a truck. Some
suggestions include the length of the truck, its height (very
important to know when it passes under another road), its cargo
capacity (volume), or its weight (important for assessing taxes).
- Each pair of students is given a pattern to cut out of
oaktag and fold up into a three-dimensional shape. They are asked to
measure the shape in as many ways as they can. They report their
findings to the class.
10. Investigate the occurrence of geometry in nature,
art, and other areas.
- Students investigate the natural shapes that
are produced by the processes of growth and physical change. They
identify some of the simple basic shapes that occur over and over
again in more complex structures. Students bring examples to class
and describe the process in writing. Some interesting examples are
honeycombs, pinecones, and seashells.
- Students make a bulletin board display of "Shapes in
the World Around Us."
- Students read the beautifully illustrated book
Listen to a Shape by Marcia Brown. The color photographs in
the book move from the occurrence in nature of simple shapes to more
complex ones. Children can be asked to describe and draw their
favorite shapes innature as a follow-up.
- Students read Shapes by Phillip Yenawine.
This carefully selected collection of works from the Museum of Modern
Art is analyzed to show how shapes contribute to the images on the
canvas. An interesting open-ended assessment activity would be to ask
the students to create their own works of art, combining the geometric
shapes they know to make similar striking images.
References
-
Brown, Marcia. Listen to a Shape. New York: Franklin
Watts, 1979.
Charosh, Mannis. Ellipse. New York: Thomas Y. Crowell,
1971.
Yenawine, Phillip. Shapes. New York: Delacourte Press,
1991.
Software
-
Logo. Many versions of Logo are commercially
available.
General reference
-
Burton, G. et al. Curriculum and Evaluation Standards for
School Mathematics: Addenda Series:
ThirdGrade Book. Reston, VA: National Council of
Teachers of Mathematics, 1992.
On-Line Resources
-
http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/
The Framework will be available at this site during
Spring 1997. In time, we hope to post additional resources
relating to this standard, such as grade-specific activities submitted
by New Jersey teachers, and to provide a forum to discuss the
Mathematics Standards.
Standard 7 - Geometry and Spatial Sense - Grades 5-6
Overview
Students can develop strong spatial sense from consistent
experiences in classroom activities that use a wide variety of
manipulatives and technology. The key components of spatial sense, as
identified in the K-12 Overview, are spatial relationships, properties
of geometric figures, geometric transformations, coordinate geometry,
geometry of measurement, geometric modeling, and reasoning.
Informal geometry and spatial visualization are vital aspects of a
mathematics program for grades 5 and 6. Middle school students
experience the fun and challenge of learning geometry through creating
plans, building models, drawing, sorting and classifying objects, and
discovering, visualizing, and representing concepts and geometric
properties. Students develop the understanding needed to function in
a three-dimensional world through explorations and investigations
organized around physical models.
Studying geometry also provides opportunities for divergent
thinking and creative problem solving while developing students'
logical thinking abilities. Geometric concepts and representations
can help students better understand number concepts while being
particularly well-suited for addressing the First Four Standards:
problem solving, reasoning, making connections, and communicating
mathematics.
Students' experiences in learning geometry should help them
perceive geometry as having a dynamically important role in their
environment and not merely as the learning of vocabulary, memorizing
definitions and formulas, and stating properties of shapes. Students,
working in groups or independently, should explore and investigate
problems in two and three dimensions, make and test conjectures,
construct and use models, drawings, and computer technology, develop
spatial sense, use inductive and deductive reasoning, and then
communicate their results with confidence and conviction. They should
be challenged to find alternative approaches and solutions.
In their study of spatial relationships, students in grades
5 and 6 further develop their understanding of projections (e.g., top,
front, and side views), perspectives (e.g., drawings made on isometric
dot paper), and maps. They also consolidate their understanding of
the concepts of symmetry (both line and rotational), congruence, and
similarity.
Students expand their understanding of properties of geometric
figures by using models to develop the concepts needed to make
abstractions and generalizations. They focus on the properties of
lines and planes as well as on those of plane and solid geometric
figures. Students at this age begin to classify geometric figures
according to common properties and develop informal definitions.
Still using models, drawings, and computer graphics, students
expand their understanding of geometric transformation,
including translations (slides), reflections (flips), rotations
(turns), and dilations (stretchers/shrinkers). At these grade levels,
the connections between transformations and congruence, similarity,
and symmetry are explored. Students also begin to use coordinate
geometry to show how figures change orientation but not shape
under transformations. For these investigations they use all four
quadrants of the coordinate plane (positive and negative numbers).
Students develop greater understanding of the geometry of
measurement as they develop strategies for finding perimeters,
areas (of rectangles and triangles), volumes, surface areas, and angle
measures. The emphasis at this level should be on looking for
different ways to find an answer, not simply on using formulas.
Students use models for many problems, look for patterns in their
answers, and form conjectures about general methods that might be
appropriate for certain types of problems. Students apply what they
are learning about areas to help them develop an understanding of the
Pythagorean Theorem.
Students continue to use geometric modeling to help them
solve a variety of problems. They explore patterns of geometric
change as well as those involving number patterns. They use geometric
representations to assist them in solving problems in discrete
mathematics. They use concrete materials, drawings, and computers to
help them visualize geometric patterns.
Students in these grade levels are beginning to develop more
sophisticated reasoning skills. In studying geometry, they
have many opportunities to make conjectures based on data they have
collected and patterns they have observed. This inductive reasoning
can then be related to what they already know; students should be
encouraged to explain their thinking and justify their responses.
Throughout fifth and sixth grade, students use concrete materials,
drawings, and computer graphics to increase the number of geometric
concepts with which they are familiar and to explore how these
concepts can be used in geometric reasoning. Students' natural
curiosity about the world provides ample opportunities for linking
mathematics with other subjects. The continued experience with two-
and three-dimensional figures provided at these grade levels helps
students build the firm foundation needed for the more formal geometry
of the secondary school.
Standard 7 - Geometry and Spatial Sense - Grades 5-6
Indicators and Activities
The cumulative progress indicators for grade 8 appear below in
boldface type. Each indicator is followed by activities which
illustrate how it can be addressed in the classroom in grades 5 and
6.
Building upon knowledge and skills gained in the preceding grades,
experiences in grades 5-6 will be such that all students:
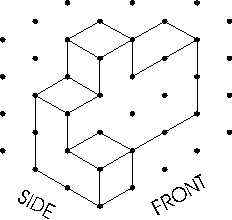
11. Relate two-dimensional and three-dimensional
geometry using shadows, perspectives, projections, and
maps.
- Students use centimeter cubes to construct a building such
as the one pictured below. They then represent their building by
drawing the base and telling how many cubes are stacked in each
portion of building.
- Students put three or four cubes together to make a solid
and draw two different projective views of the solid on triangle dot
paper, such as those shown below.
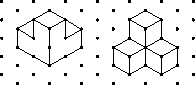
- Students copy pictures of solids drawn on triangle dot
paper such as the one below, build the solids, and find their
volumes.
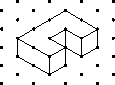
- Students use circles and rectangles to make
3-dimensional models of cylinders, cones, prisms, and other
solids.
- Students predict and sketch the shapes of the faces of a
pyramid, or, given a flat design for a box, predict what it will look
like when put together.
12. Understand and apply the concepts of symmetry,
similarity, and congruence.
- Students compare different Logo procedures for drawing
similar rectangles.
- Students look for examples of congruent figures (same size
and shape) in the environment.
- Students explore symmetry by looking at the designs formed
by placing a mirror on a pattern block design somewhere other than the
line of symmetry, or by folding paper more than one time. They
identify the symmetry in wallpaper or giftwrap designs. They also
identify the rotational symmetry found in a pinwheel (e.g., 90 degrees).
(The figure matches itself by turning rather than by flipping or
folding.)
- Students build scale models to investigate similarity.
They recognize that figures which have the same shape but different
sizes are similar.
13. Identify, describe, compare, and classify plane
and solid geometric figures.
- Students are given a sheet of 3 x 3 dot paper grids. They
find and draw as many noncongruent quadrilaterals as they can, using a
different set of nine dots for each figure; altogether sixteen
different quadrilaterals (pictured below) can be formed.
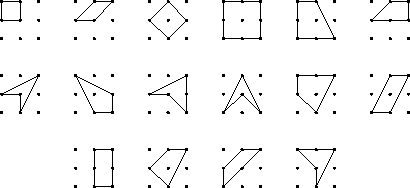
A nice open-ended approach to assessment of their understanding and
comfort with properties of geometric figures is to ask them to sort
these quadrilaterals in different ways, including concave vs. convex,
by angle sizes, by area, by symmetry, and so on. See how many ways
they can devise.
- Students trace a figure onto several transparencies;
figures such as squares, rectangles, parallelograms, rhombuses,
trapezoids, kites, and arrowheads can be used. Then they draw the
lines of symmetry for the figure. They rotate, translate, and flip
the transparencies and compare them to an original transparency to
investigate such properties as: the number of congruent sides in the
figure, the number of parallel sides in the figure, whether the
diagonals are congruent, whether the diagonals bisect each other,
whether the diagonals are perpendicular, and whether the figure has
half-turn symmetry (180 degrees). They write about their findings and
explain their reasoning.
- Students use Logo to investigate the sum of the measures of
the exterior angles of any polygon (360 degrees) and the angle measure
of each exterior angle of a regular polygon.
- Students select straws cut to five different lengths (for
example, from one inch to five inches) and form as many different
triangles as they can, recording the results. They sort the triangles
into groups with 0, 2, or 3 equal sides and label the groups as
scalene, isosceles, and equilateral triangles.
14. Understand the properties of lines and planes,
including parallel and perpendicular lines and planes, and
intersecting lines and planes and their angles of incidence.
- Students use index cards with slits cut in them to build
models of two planes that are parallel or two planes that intersect
(in a line).
- Students use toothpicks to explore how two lines might be
related to each other (parallel, intersecting, perpendicular, the same
line).
- Students find examples of parallel lines and planes,
perpendicular lines and planes, and intersecting lines and planes with
different angles in their environment.
15. Explore the relationships among geometric
transformations (translations, reflections, rotations, and
dilations), tessellations (tilings), and congruence and
similarity.
- Students read and examine The World of
M.C. Escher or any other collection of M.C. Escher's work to
find and describe the tessellations in them. Transformations of
tessellating polygons are then performed by the students to make their
own artwork.
- Students create a design on a geoboard, sketch their
design, move the pattern to a new spot by using a specified
transformation, and sketch the result.
- Students investigate wallpaper, fabric, and gift wrap
designs. They create a template for a unit figure which they will use
to create individual border designs for their classroom. Each student
presents her/his design to the class, describing the transformations
used to create the design.
- Working in small groups, students tile a portion of their
desktop using oak-tag copies they have cut of a shape they have
created by taping together two pattern blocks. Each group presents
its results. The teacher then asks the students to compare the
results of the different groups and identify examples of the different
transformations used.
- Students investigate how transformations affect the size,
shape, and orientation of geometric figures. A reflection or flip is
a mirror image. A translation or slide moves a figure a specified
distance and direction along a straight line. A rotation or turn is a
turning motion of a specified amount and direction about a fixed
point, the center. These transformations do not change the size and
shape of the original figure. However, a dilation enlarges
(stretches) or reduces (shrinks) a figure, producing a new figure with
the same shape but a different size.
- Students use Tesselmania! software to
manipulate and transform colorful shapes on the computer screen and
create complex tessellations.
- Students continue to look for and report on
transformations they find in the world around them.
16. Develop, understand, and apply a variety of
strategies for determining perimeter, area, surface area, angle
measure, and volume.
- Students are given a transparent square grid to place over
a worksheet with triangles drawn on it. Using the grid to measure,
they find the base, height, and area of each triangle, recording their
findings in a table. They discuss patterns that they see, developing
their own formula to find areas of triangles.
- Students find the perimeter of a figure by taping a string
around it and then untaping and measuring the string. For something
large, like the classroom, they might construct and use a trundle
wheel.
- Students first estimate the perimeter (or area, volume, or
surface area) of a classroom object, then measure it, determine its
perimeter, and compare their answers to their estimates. Objects
which might be used include books, desks, closets, doors, or
windows.
- Students use various same-shape pattern blocks
and arrange as many as are needed around a point to complete a circle.
They discover the size of each angle since there are 360 degrees in one
circle. For example, if it takes six (green) triangles, then each
angle must be 60 degrees (360 degrees ÷ 6).
-
 Students are given a sheet with rectilinear figures (only right
angles) on it, such as the letter "E" at the right, and a
transparent square centimeter grid that they can place over each of
the figures. By counting the squares, they can find the area of each
figure; by counting the number of units around it, they can determine
its perimeter.
Students are given a sheet with rectilinear figures (only right
angles) on it, such as the letter "E" at the right, and a
transparent square centimeter grid that they can place over each of
the figures. By counting the squares, they can find the area of each
figure; by counting the number of units around it, they can determine
its perimeter.
- Students use centimeter cubes to build a structure such as
the one shown below and then count the cubes to find the volume of the
structure.

- Students bring cereal boxes from home, cut them apart, and
determine their surface areas.
- Students find the volumes of different backpacks by using
familiar solids to approximate their shape. They compare their
results and write about which backpack they think would be
"best" and why.
17. Understand and apply the Pythagorean
Theorem.
- Students construct squares on each side of a right triangle
on a geoboard and find the area of each square. They repeat this
process using several different triangles, recording their results in
a table. Then they look for patterns in the table.
- Students measure the distance diagonally from first to
third base on a baseball field and compare it to the distance run by a
player who goes from first to second to third. Theynote that it is a
shorter distance diagonally across the field than it is along the two
sides. They repeat this type of measuring activity for other squares
and rectangles, noting their results in a table and discussing any
patterns they see. They calculate the square of each of the three
sides of each triangle, record their results in a table, and look for
patterns.
18. Explore patterns produced by processes of
geometric change, relating iteration, approximation, and
fractals.
- Students use the reducing and/or enlarging feature on a
copier to explore repeated reductions/enlargements by the same factor
(iteration).
- Students investigate the natural shapes that are produced
by growth. They look at how nature produces complex structures in
which basic shapes occur over and over. For example, spider webs,
honeycombs, pineapples, pinecones, nautilus shells, and snowflakes
grow larger in a systematic way (iteration).
19. Investigate, explore, and describe the geometry in
nature and real-world applications, using models,
manipulatives, and appropriate technology.
- Students design a three-dimensional
geometric sculpture. Some may want to find plans for making a
geodesic dome and construct it out of gumdrops and toothpicks.
- Students work through the Two-Toned
Towers lesson that is described in the First Four Standards of
this Framework. They use models to determine how many
different towers can be built using four blocks of two different
colors.
- Groups of students working together design a doghouse to
be built from a 4' x 8' sheet of plywood. They construct a scale
model of their design from oaktag.
- Students use computer programs like The Geometry
PreSupposer to explore the relationships of sides of polygons or
properties of quadrilaterals.
- Assessments that make use of manipulatives and
computer software allow students to demonstrate their knowledge and
understanding of geometry. The results of performance tasks such as
the following would be appropriate for a portfolio: Make as many
different sized squares as you can on a
fivebyfive geoboard. Create a tessellation pattern with
pattern blocks or Tessellmania! software that uses slides,
flips, and turns.
- Students select a country or culture, research the use of
specific geometric patterns in that culture, and make a report to the
class.
- Specific manipulatives that may be helpful for geometry
include pattern blocks, color tiles, linking cubes, centimeter cubes,
tangrams, geoboards, links, and templates. Computer programs such as
Logo, Shape Up!, Elastic Lines, Building Perspective, or The
Factory may also be helpful.
References
-
Looher, J. L, Ed. The World of M. C. Escher. New York:
Abradale Press, Harry N. Abrams, Inc., 1971, 1988.
Software
-
Building Perspective. Sunburst Communications.
Elastic Lines. Sunburst Communications.
Logo. Many versions of Logo are commercially
available.
Shape Up! Sunburst Communications.
Tesselmania! Minnesota Educational Computing Consortium
(MECC).
The Factory. Sunburst Communications.
The Geometry PreSupposer. Sunburst Communications.
General references
-
Diggins, Julia. String, Straightedge, and Shadow: The Story
of Geometry. New York: Viking Press, 1965.
Geddes, D. Curriculum and Evaluation Standards for School
Mathematics: Addenda Series: Geometry
in the Middle Grades. Reston, VA: National Council of Teachers
of Mathematics, 1992.
On-Line Resources
-
http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/
The Framework will be available at this site during
Spring 1997. In time, we hope to post additional resources
relating to this standard, such as grade-specific activities submitted
by New Jersey teachers, and to provide a forum to discuss the
Mathematics Standards.
Standard 7 - Geometry and Spatial Sense - Grades 7-8
Overview
Students can develop strong spatial sense from consistent
experiences in classroom activities that use a wide variety of
manipulatives and technology. The key components of spatial sense, as
identified in the K-12 Overview, are spatial relationships, properties
of geometric figures, geometric transformations, coordinate geometry,
geometry of measurement, geometric modeling, and reasoning.
Students in grades 7 and 8 learn geometry by: engaging in
activities and spatial experiences organized around physical models,
modeling, mapping, and measuring; discovering geometric relationships
by using mathematical procedures such as drawing, sorting,
classifying, transforming, and finding patterns; and solving geometric
problems.
Building explicit linkages among mathematical topics is especially
important with respect to geometry, since geometric concepts
contribute to students' understanding of other topics in
mathematics. For example, the number line provides a way of
representing whole numbers, fractions, decimals, integers, lengths,
and probability. Regions are used in developing understanding of
multiplication, fraction concepts, area, and percent. The coordinate
plane is used to relate geometry to algebra and functions. Similar
triangles are used in connection with ratio and proportion.
Students continue to develop their understanding of spatial
relationships by examining projections (viewing objects from
different perspectives), shadows, perspectives, and maps. They apply
the understanding developed in earlier grades to solve problems
involving congruence, similarity, and symmetry.
Students begin to explore the logical interrelationships among
previously-discovered properties of geometric figures at
these grade levels. They extend their work with two-dimensional
figures to include circles as well as special quadrilaterals. They
continue to work with various polygons, lines, planes, and
three-dimensional figures such as cubes, prisms, cylinders, cones,
pyramids, and spheres.
The study of geometric transformations continues as well at
these grade levels, becoming more closely linked to the study of
algebraic concepts and coordinate geometry in all four
quadrants. Students begin to represent transformations and/or their
results symbolically. They also continue to analyze the relationships
between figures and their transformations, considering congruence,
similarity, and symmetry.
The geometry of measurement is extended to circles,
cylinders, cones, and spheres in these grades. Students learn about
pi and use it in a variety of contexts. They explore different
ways to find perimeters, circumferences, areas, volumes, surface
areas, and angle measures. They also develop and apply the
Pythagorean Theorem. The emphasis is on understanding the processes
used and on recording the procedures in a formula; students should not
simply be given a formula and be expected to use it.
Students continue to use geometric modeling to represent
problem situations in different areas. Drawings of various types are
particularly useful to students in understanding the context of
problems. Number lines, coordinate planes, regions, and similar
triangles help students to visualize numerical situations. Especially
important are the patterns produced by change processes, including
growth and decay.
Students further develop their reasoning skills by making
conjectures as they explore relationships among various shapes and
polygons. For example, as students learn about the midpoints of line
segments, they can make guesses about the shapes produced by
connecting midpoints of consecutive sides of quadrilaterals. By
testing their hypotheses with drawings they make (by hand or using a
computer), the students come to actually see the possibilities that
can exist. The informal arguments that students develop at these grade
levels are important precursors to the more formal study of geometry
in high school.
The emphasis in grades 7 and 8 should be on investigating and using
geometric ideas and relationships, not on memorizing definitions and
formulas. A special feature of these grade levels is that students
are preparing to take the New Jersey Early Warning Test (EWT). Many
of the items in the Measurement and Geometry Cluster of the EWT will
ask students to use those geometric ideas and relationships to solve
problems - not simply to recall formulas. Indeed, the formulas
needed for the problems are given to them on the Reference Sheet that
accompanies the test. In their general classroom activity, as well as
in preparation for the EWT, students should use a variety of concrete
materials to model and analyze situations in two and three dimensions.
They should use drawings that they make, either by hand or with the
aid of a computer, to further examine geometric situations or to
record what they have done. Geometry approached in this way can be fun
and challenging for students.
Standard 7 - Geometry and Spatial Sense - Grades 7-8
Indicators and Activities
The cumulative progress indicators for grade 8 appear below in
boldface type. Each indicator is followed by activities which
illustrate how it can be addressed in the classroom in grades 7 and
8.
Building upon knowledge and skills gained in the preceding grades,
experiences in grades 7-8 will be such that all students:
11. Relate two-dimensional and three-dimensional
geometry using shadows, perspectives, projections, and
maps.
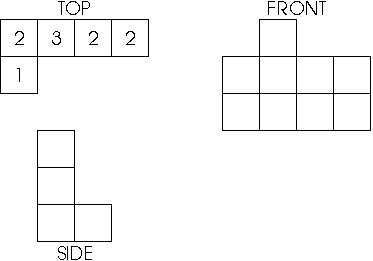
- Students build and draw solids made of cubes. They learn
to build solids from drawings and to make their own drawings of
solids. Among the drawings with which they should be familiar are the
two-dimensional flat view from top, front, and side; the
three-dimensional corner view; and the map view showing the base of
the building with the number of cubes in each stack. For example,
they can build the solid below; presented here are a three-dimensional
corner view, a flat view, and a map view.
- Students predict what the intersections of a plane with a
cylinder, cone, or sphere will be. Then they slice clay models to
verify their predictions.
- Students use cubes made of clear plexiglas and partially
filled with colored water to investigate cross sections of a plane
with a cube. They try to tilt the cube so that the surface of the
water forms various shapes, such as a square, a rectangle that is not
a square, a trapezoid, a hexagon, and others.
12. Understand and apply the concepts of symmetry,
similarity, and congruence.
- Students create three-dimensional symmetric designs using
cubes, cylinders, pyramids, cones, and spheres.
- Students build scale models of the classroom, using
similarity to help them determine the appropriate measures of the
models.
- Students use compasses and straight-edges to construct
congruent line segments and angles.
- Students work through the Sketching
Similarities lesson that is described in the First Four Standards
of this Framework. Students use a computer program and various
similar figures to discover that corresponding angles have equal
measures and corresponding sides have equal ratios.
13. Identify, describe, compare, and classify plane
and solid geometric figures.
- Students use toothpicks to construct as many different
types of triangles as possible, where each side of the triangles
consists of between one and five toothpicks. They record their
findings in a table, showing how many triangles are scalene,
isosceles, equilateral, right, and obtuse. They also indicate which
combinations of sides are impossible.
- Students sort collections of quadrilaterals according to
the number of lines of symmetry that each has.
- Students play clue games designed to help them distinguish
between necessary and sufficient conditions in describing a shape.
For example: If you want to challenge your friend to
identify a square by giving a set of clues, which minimum set of clues
would you select from the list below? Explain your
selection. Is it possible to select a different minimum
set of clues? Explain.
-
| - 4 right angles |
- all angles are 90 degrees |
| - 4 sides |
- all sides of equal length |
| - all angles congruent |
- opposite angles congruent |
| - opposite sides parallel |
- simple closed curve |
- Openended assessment items like those used on
the Early Warning Test can always be used to provoke discussion and
classroom activity. One of the sample items in the New Jersey
Department of Education's Mathematics Instructional Guide
(MG3) shows several figures and asks which of them can be put together
to form a square. The developmental and extension activities provided
there offer good suggestions for manipulative and transformation
tasks.
- Students work through the A Sure Thing !? lesson
that is described in the Introduction to this Framework. They
investigate the relationship among the measures of the interior angles
of a triangle by cutting out arbitrary triangles, tearing them into
three pieces so that each corner is intact, and fitting the corners
around a single point to make a straight angle.
- Students use diagrams to demonstrate the relationships
among properties. For example, they might draw a diagram to show the
logical relationship of ideas leading to the angle sum for a
quadrilateral, or, as below, to clarify the relationship among
different types of quadrilaterals.
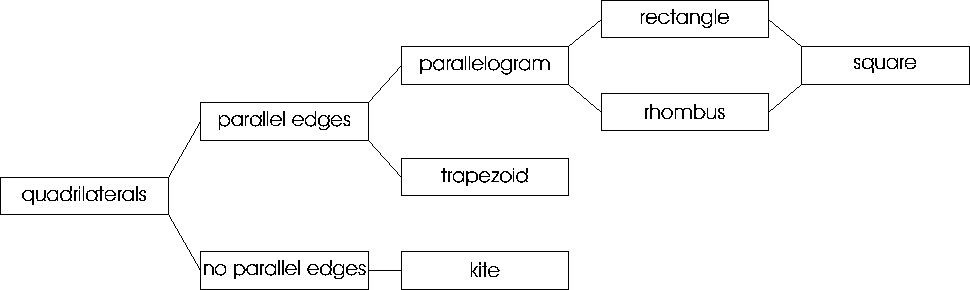
14. Understand the properties of lines and planes,
including parallel and perpendicular lines and planes, and
intersecting lines and planes and their angles of incidence.
- Students build a model of a cube, connect a midpoint of an
edge with a midpoint of another edge, and then connect two other
midpoints of edges to each other. They describe the relationships of
the segments they have constructed. They change one of the line
segments to another location and repeat the activity.
- Students identify congruent angles on a parallelogram grid,
using their results to develop conjectures about alternate interior
angles and corresponding angles of parallel lines and about opposite
angles of a parallelogram.
- Working in groups, students review geometric vocabulary by
sorting words written on index cards into groups and explaining their
reasons for setting up the groups in the way that they did.
15. Explore the relationships among geometric
transformations (translations, reflections, rotations, and
dilations), tessellations (tilings), and congruence and
similarity.
-
 Students use the "nibble" technique to create a shape
which will tessellate the plane, that is, copies of this shape will
fit together to cover a planar surface like a sheet of white oak-tag.
Start with a square, cut off a "nibble" along the top or
bottom edge of the square and
translate the nibble vertically to the opposite edge of the square;
the "nibble" will then be outside the boundary of the
original square. Take a "nibble" from the right or left
edge of the square and translate it horizontally to the opposite edge
of the square. Trace this shape repeatedly onto a sheet of white
oak-tag, by interlocking the pattern, and decorate the copies of the
shape. Attempt this process several times until a pleasing shape is
created.
Students use the "nibble" technique to create a shape
which will tessellate the plane, that is, copies of this shape will
fit together to cover a planar surface like a sheet of white oak-tag.
Start with a square, cut off a "nibble" along the top or
bottom edge of the square and
translate the nibble vertically to the opposite edge of the square;
the "nibble" will then be outside the boundary of the
original square. Take a "nibble" from the right or left
edge of the square and translate it horizontally to the opposite edge
of the square. Trace this shape repeatedly onto a sheet of white
oak-tag, by interlocking the pattern, and decorate the copies of the
shape. Attempt this process several times until a pleasing shape is
created.
- Students analyze the patterns found in Arabic designs such
as tiled floors and walls in Spain, identifying figures that represent
translations, reflections, and rotations. Then they generate their
own tile designs using basic geometric shapes. They can create their
own tile patterns using Tesselmania! software.
- Students apply transformations to figures drawn on
coordinate grids, record the coordinates of the original figure and
its image, and look for patterns. They express these patterns
verbally and symbolically. For example, flipping a point across the
x-axis changes the sign of the y-coordinate so that the point (x,y)
moves to (x,-y).
- Students practice doing geometric
transformations mentally by using the Geometric Golfer or
similar computer software. These programs present a series of puzzles
in which there is an object shape and a target shape.
The task is to use the fewest transformations possible to change the
object shape so that it is congruent to the target
shape. In the golf game, the object is a ball and the target is a
hole.
16. Develop, understand, and apply a variety of
strategies for determining perimeter, area, surface area, angle
measure, and volume.
- Students use a paper fastener to connect two models of rays
to form angles of different sizes. They estimate the correct
position, then measure their guess with a protractor to see how close
they were.
- Students are given a parallelogram-shaped piece of oak-tag
and asked to cut it apart and arrange the parts so that it is easy to
find its area. Their solutions are expressed verbally and
symbolically. This same process is repeated for a trapezoid.
- Students bring cans from home, arrange them by
estimated volume from smallest to largest, determine the actual
volumes by measuring and computing, and compare these results to their
estimates.
- Good conceptual assessment items designed to
measure students' understanding of area frequently ask the
students to find the area remaining in one figure after the area of
another figure has been removed. One sample item from the New Jersey
Department of Education's Mathematics Instructional Guide,
for example, asks students to find the area of a circular path that
surrounds a circular flower garden (MG1). Problems like this one are
not only good practice for tests like the Early Warning Test but can
also be used as informal assessments by teachers who listen carefully
to their students' discussions about them.
- Students work through the Rod Dogs lesson
that is described in the First Four Standards of this
Framework. Students determine the effects of increasing the
dimensions of an object on its surface area and volume.
17. Understand and apply the Pythagorean
Theorem.
- Students draw right triangles on graph paper with legs of
specified lengths and measure the lengths of their hypotenuses. They
record their results in a chart and look for patterns.
- Students create a small right triangle in the middle of a
ten-by-ten geoboard or on dot paper and then build squares on each
side of the triangle. They record the areas of the squares and look
for a relationship involving these areas.
- Students use tangram pieces to build squares on each side
of the middle-sized triangular tangram piece. They then describe the
relationship among the areas of the three squares.
18. Explore patterns produced by processes of
geometric change, relating iteration, approximation, and
fractals.
- Students use the reducing and/or enlarging feature on a
copier to explore repeated reductions/enlargements by the same factor
(iteration).
- Students learn about the natural shapes that are produced
by growth. They investigate how nature produces complex structures in
which basic shapes occur over and over. For example, spider webs,
honeycombs, and snowflakes grow larger in a systematic way
(iteration). Students measure the age of a tree by looking at its
rings; this illustrates approximation. Students produce geometric
designs that illustrate these principles, as well as fractals, where
miniature versions of the entire design are evident within a
smallportion of the design.
- Students view the slides which accompany the
activity book, Fractals for the Classroom, Vol. 1, and
determine why each picture might have been included in a book about
fractals.
- Students make a table showing the perimeter of a Koch
snowflake (a type of fractal) and its area at each stage. They
discuss the patterns in the table. This is an example where the
perimeter increases without bound but the area approaches a
limit.
|
| Stage |
Perimeter |
Area |
| 0 |
3 |
1 |
| 1 |
4 |
4/3 |
| 2 |
16/3 |
40/27 |
| 3 |
|
|
| 4 |
|
|
|
19. Investigate, explore, and describe geometry in
nature and real-world applications, using models,
manipulatives, and appropriate technology.
- Some students read and prepare a report and
presentation to the class on String, Straightedge, and
Shadow: The Story of Geometry by Julia Diggins. Starting with a
chapter about the presence of geometry in nature, this story traces
the history of geometric discoveries from the invention of early
measuring instruments.
- Students model decay in a bacterial culture by cutting a
sheet of grid paper in half repeatedly and recording the area of each
rectangle in a table. They then graph the number of cuts versus the
area to see an example of exponential decay.
- Students investigate the golden ratio
((1 + sqrt(5))/2) and its application to architecture (such as the
Parthenon), designs of everyday objects such as index cards and
picture frames, and its occurrence in pinecones, pineapples, and
sunflower seeds.
- Students write about why manufacturers make specially
designed containers for packaging their products, indicating how the
idea of tessellations might be important in the designs.
- Students use a computer program such as The Geometry
PreSupposer to investigate the relationship between the lengths of
the sides and the measures of the angles in isosceles, scalene, and
equilateral triangles.
- Groups of students prepare slide shows using slides from
Geometry in Our World to illustrate the connections between
geometry, science, and art.
- Pairs of students build kites of different shapes,
explaining to the class why they chose a particular shape. Each
student predicts which kite will fly highest, writing the prediction
in his/her journal. The class flies all of the kites, recording the
heights of each by using a clinometer and similar triangles.
- Students watch the video Donald in Mathmagic
Land. Although getting a bit dated, thisvideo still thrills most
viewers as Donald Duck encounters many animated applications of
geometry. Students then form teams which focus on an aspect of the
video and do further research on that application.
- Students read and choose projects to make from
the book Origami, Japanese Paper Folding by Florence
Sakade or some other origami instruction books. The detailed
instructions usually given in such books are rich in mathematical
language and discussions among the students should provide a setting
for the use of much geometric terminology.
References
-
Diggins, Julia. String, Straightedge, and Shadow: The Story
of Geometry. New York: Viking Press, 1965.
Engelhardt, J., Ed. Geometry in Our World. Reston, VA:
National Council of Teachers of Mathematics, 1992.
New Jersey Department of Education. Mathematics Instructional
Guide. D. Varygiannes, Coord. Trenton: 1996.
Peitgen, Heinz-Otto, et al. Fractals for the Classroom:
Strategic Activities, Vol. 1. Reston, VA: National Council of
Teachers of Mathematics, and New York: Springer-Verlag, 1991.
Sakade, Florence. Origami, Japanese Paper Folding.
Rutland, VT: Charles E. Tuttle Co., 1957.
Software
-
Geometric Golfer. Minnesota Educational Computing
Consortium (MECC).
The Geometry PreSupposer. Sunburst Communications.
Tesselmania! Minnesota Educational Computing Consortium
(MECC).
Video
-
Donald in Mathmagic Land. Walt Disney Studios. Los
Angeles: The Walt Disney Company, 1959.
General references
-
Geddes, D. Curriculum and Evaluation Standards for School
Mathematics: Addenda Series:
Geometry in the Middle Grades. Reston, VA: National
Council of Teachers of Mathematics, 1992.
Owens, D. T., Ed. Research Ideas for the Classroom: Middle
Grades Mathematics. New York: MacMillan, 1993.
On-Line Resources
-
http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/
The Framework will be available at this site during
Spring 1997. In time, we hope to post additional resources
relating to this standard, such as grade-specific activities submitted
by New Jersey teachers, and to provide a forum to discuss the
Mathematics Standards.
Standard 7 - Geometry and Spatial Sense - Grades 9-12
Overview
Students can develop a strong spatial sense from consistent
experiences in classroom activities which use a wide variety of
manipulatives and technology. The key components of this spatial
sense, as identified in the K-12 Overview, are spatial relationships,
properties of geometric figures, geometric transformations, coordinate
geometry, geometry of measurement, geometric modeling, and
reasoning.
Geometry has historically held an important role in high school
mathematics, primarily through its focus on deductive reasoning and
proof; developing skills in deductive reasoning, learning how to
construct proofs, and understanding geometric properties are important
outcomes of the high school geometry course. Equally important,
however, is the continued development of visualization skills,
pictorial representations, and applications of geometric ideas since
geometry helps students represent and describe the world in which they
live and answer questions about natural, physical, and social
phenomena.
Deductive reasoning is highly dependent upon understanding and
communication skills. In fact, mathematics can be considered as a
language - a language of patterns. This language of mathematics
must be meaningful if students are to discuss mathematics, construct
arguments, and apply geometry productively. Communication and
language play a critical role in helping students to construct links
between their informal, intuitive geometric notions and the more
abstract language and symbolism of high school geometry.
Geometry describes the real world from several viewpoints. One
viewpoint is that of standard Euclidean geometry - a deductive
system developed from basic axioms. Other widely used viewpoints are
those of coordinate geometry, transformational geometry, and vector
geometry. The interplay between geometry and algebra strengthens the
students' ability to formulate and analyze problems from
situations both within and outside mathematics. Although students
will at times work separately in synthetic, coordinate,
transformational, and vector geometry, they should also have many
opportunities to compare, contrast, and translate among these systems.
Further, students should learn that certain types of problems are
often solved more easily in one specific system than another specific
system.
Visualization and pictorial representation are also important
aspects of a high school geometry course. Students should have
opportunities to visualize and work with two- and three-dimensional
figures in order to develop spatial skills fundamental to everyday
life and to many careers. By using physical models and other
real-world objects, students can develop a strong base for geometric
intuition. They can then draw upon these experiences and intuitions
when working with abstract ideas.
The goal of high school geometry includes applying geometric ideas
to problems in a variety of areas. Each student must develop the
ability to solve problems if he or she is to become a productive
citizen. Instruction thus must begin with problem situations -
not only exercises to be accomplished independently but also problems
to be solved in small groups or by the entire class working
cooperatively.
Applications of mathematics have changed dramatically over the last
twenty years, primarily due to rapid advances in technology. Geometry
has, in fact, become more important to students because of
computergraphics. Thus, calculators and computers are appropriate and
necessary tools in learning geometry.
Students in high school continue to develop their understanding of
spatial relationships. They construct models from
two-dimensional representations of objects, they interpret two- and
three-dimensional representations of geometric objects, and they
construct two-dimensional representations of actual objects.
Students formalize their understanding of properties of
geometric figures, using known properties to deduce new
relationships. Specific figures which are studied include polygons,
circles, prisms, cylinders, pyramids, cones, and spheres. Properties
considered should include congruence, similarity, symmetry, measures
of angles (especially special relationships such as supplementary and
complementary angles), parallelism, and perpendicularity.
In high school, students apply the principles of geometric
transformations and coordinate geometry that they learned
in the earlier grades, using these to help develop further
understanding of geometric concepts and to establish justifications
for conclusions inferred about geometric objects and their
relationships. They also begin to use vectors to represent geometric
situations.
The geometry of measurement is extended in the high school
grades to include formalizing procedures for finding perimeters,
circumferences, areas, volumes, and surface areas, and solving
indirect measurement problems using trigonometric ratios. Students
should also use trigonometric functions to model periodic phenomena,
establishing an important connection between geometry and algebra.
Students use a variety of geometric representations in geometric
modeling at these grade levels, such as graphs of algebraic
functions on coordinate grids, networks composed of vertices and
edges, vectors, transformations, and right triangles to solve problems
involving trigonometry. They also explore and analyze further the
patterns produced by geometric change.
Deductive reasoning takes on an increasingly important role
in the high school years. Students use inductive reasoning as they
look for patterns and make conjectures; they use deductive reasoning
to justify their conjectures and present reasonable explanations.
Standard 7 - Geometry and Spatial Sense - Grades 9-12
Indicators and Activities
The cumulative progress indicators for grade 12 appear below in
boldface type. Each indicator is followed by activities which
illustrate how it can be addressed in the classroom in grades 9, 10,
11 and 12.
Building upon knowledge and skills gained in the preceding grades,
experiences in grades 9-12 will be such that all students:
16*. Develop, understand, and apply a
variety of strategies for determining perimeter, area, surface
area, angle measure, and volume.
- Students find volumes of objects formed by
combining geometric figures and develop formulas describing what they
have done. For example, they might generate a formula for finding the
volume of a silo composed of a cylinder of specified radius and height
topped by a hemisphere of the same radius.
- Students construct models to show how the volume
of a pyramid with a square base and height equal to a side of the base
is related to the volume of a cube with the same base.
- Students develop and use a spreadsheet to
determine what the dimensions should be for a cylinder with a fixed
volume, in order to minimize the surface area. Similarly, they
investigate what should be the dimensions for a rectangle having a
fixed perimeter in order to maximize the enclosed area. They discuss
how the symmetry of these figures relates to the
solutions.
19*. Investigate, explore, and
describe geometry in nature and real-world applications, using
models, manipulatives, and appropriate technology.
- Students use a computer-aided design (CAD)
program to investigate rotations of objects in three
dimensions.
- Students use The Geometric SuperSupposer
to measure components of shapes and make observations. For example,
they might construct parallelograms and measure sides, angles, and
diagonals, observing that opposite sides are congruent, as are
opposite angles, and that diagonals bisect each other.
- Students use The Geometer's
Sketchpad to investigate the effects of rotating a triangle about
a fixed point.
- Students use commercial materials such as
GeoShapes or Polydrons to construct three-dimensional geometric
figures. They make tables concerning the number of vertices, edges,
and faces in each solid. They measure the figures to determine their
surface areas and volumes. They lay the patterns out flat to examine
the nets of each solid. [A net is aflat shape which when folded along
indicated lines will produce a three-dimensional object; for example,
six identical squares joined in the shape of a cross can be folded to
form a cube. Tabs added to the net facilitate attaching appropriate
edges so that the shape remains three-dimensional.]
- Students work through the Ice Cones
lesson that is described in the First Four Standards of this
Framework. Students create a variety of paper cones out of
circles with radius 10 inches which are cut along a radius. They use
graphing calculators to find the maximum volume of such
cones.
- Students copy geometric designs using compass
and straightedge, and generate their own designs.
- Students investigate wallpaper patterns,
classifying them according to the transformations used. They study
the structure of crystals from a geometric perspective.
20. Understand and apply properties involving angles,
parallel lines, and perpendicular lines.
- Students make tessellations with an assortment of different
triangles, noting the variety of geometric patterns that are formed,
including parallel lines, congruent angles, congruent triangles,
similar triangles, parallelograms, and trapezoids.
- Students identify congruent angles on a parallelogram grid,
and use their results to develop conjectures about alternate interior
angles, corresponding angles of parallel lines, and opposite angles of
a parallelogram.
- Working together, students review geometric vocabulary by
sorting words written on index cards into groups and explaining their
reasons for creating the groups they did. For example, they might
place "parallelogram," "rhombus,"
"square," and "rectangle" in one group (since they
are all parallelograms) and place "kite" and
"trapezoid" in another group (since they are not
parallelograms).
- Students find a variety of strategies for
demonstrating that the sum of the measures of the angles of a triangle
is 180 degrees. Some use protractors and measure a pencil-and-paper
figure, others create a triangle with Geometer's
Sketchpad software and post the measures of the angles before
dragging it from a vertex to notice that the sum always remains the
same, and still others use a method that requires tearing each of the
corners from an oaktag triangle and then fitting them together to make
a line.
21. Analyze properties of three-dimensional shapes by
constructing models and by drawing and interpreting
two-dimensional representations of them.
- Pairs of students work together to describe and draw
geometric figures. One student is given a picture involving one or
more geometric figures and must describe the drawing to the other
student without using the names of the figures. The second student,
without seeing the figure, must visualize and represent the
picture.
- Students create wind-up posterboard models of rotational
three-dimensional solids. They cut out a plane figure such as a
circle or a rectangle from posterboard, punch two holes in it near its
edges, thread a cut rubberband through the holes, and attach the ends
of the rubberband to the ends of a coathanger from which the
horizontal wire has been removed. They then twist the rubber band to
wind up the figure and release to "show" the solid.
- Students use isometric dot paper to sketch figures made up
of cubes. They also sketch top, front, and side views (projections)
of the figure.
- One long-term project that some high school
teachers use for assessment is the following: Using a variety of means
and materials, students begin by constructing models of the Platonic
solids and other three dimensional geometric figures. They are then
challenged to work in teams to find a relationship among the number of
faces, vertices, and edges that holds for all of the solids
(Euler's Formula: F + V - E = 2).
- Students read Flatland: A Romance of Many
Dimensions by Edwin Abbott, a fascinating and imaginative story
about life in a two-dimensional world.
- Students use a computer-aided design (CAD)
program to investigate rotations of objects in three
dimensions.
22. Use transformations, coordinates, and vectors to
solve problems in Euclidean geometry.
- Students construct a polygon that outlines the top view of
their school. They are asked to imagine that they are architects who
need to send this outline by computer to a builder who has no graphics
imaging capabilities. They develop strategies for sending this
information to the builder. One group locates one corner of the
building at the origin and determines the coordinates for the other
vertices. Another group uses vectors to tell the builder what
direction to proceed from the initial corner located at the
origin.
- Students work on the question of where a power transformer
should be located on a line so that the length of the cable needed to
run to two points not on that line is minimized. They find that if
the two points are on the same side of the line, then by using
reflections they can construct a straight line that crosses the given
line at the desired location.
- Students first determine the coordinates for the vertices
of a parallelogram, a rhombus, a rectangle, an isosceles trapezoid,
and a square with one vertex at the origin and a side along the
x-axis. They then work in groups to determine where the coordinate
system should be placed to simplify the coordinate selection for a
kite, a rhombus, and a square.
- Students draw two congruent triangles anywhere in the plane
and determine the minimum number of reflections needed to map one onto
the other.
- Students draw a triangle on graph paper and then find the
image of the triangle when the coordinates of each vertex are
multiplied by various constants. They draw each resulting triangle
and determine its area. They make a table of their results and look
for relationships between the constants used for dilation and the
ratios of the areas.
- Students use a Mira (Reflecta) to find the center of a
circle, to draw the perpendicular bisectors of a line segment, or to
draw the medians of a triangle.
- Students apply transformations to figures drawn on
coordinate grids, record the coordinates of the original figure and
its image, and look for patterns. They express these patterns
verbally and symbolically. For example, flipping a point across the
x-axis changes the sign of the y-coordinate so that the point (x,y)
moves to (x, -y).
- Given the equation of a line, students plot the
line on a coordinate grid and then shift the line according to a given
translation. They then determine the equation of the resulting line.
After doing several such problems, students identify patterns that
they have found and write conjectures.
- Students work through the Building
Parabolas lesson that is described in the First Four Standards of
this Framework. They investigate the effects of various
coefficients on the general shape of a parabola and connect these to
geometric transformations.
23. Use basic trigonometric ratios to solve problems
involving indirect measurement.
- Students use trigonometric ratios to determine distances
which cannot be measured directly, such as the distance between two
points on opposite sides of a chasm.
- Students investigate how the paths of tunnels are
determined so that people digging from each end wind up in the same
place.
- Students use trigonometry to determine the cloud ceiling at
night by directing a light (kept in a narrow beam by a parabolic
reflector) toward the clouds. An observer at a specified distance
measures the angle of elevation to the point at which the light is
reflected from the cloud.
- Students plot the average high temperature for each month
over the course of five years to see an example of a periodic
function. They discuss what types of functions might be appropriate
to represent this relationship.
24. Solve real-world and mathematical problems using
geometric models.
- Students visit a construction site where the
"framing" step of a building process is taking place. They
note where congruence occurs (such as in the beams of the roof, where
angles must be congruent). They write about why congruence is
essential to buildings and other structures.
- Students use paper fasteners and tagboard strips with a
hole punched near each end to investigate the rigidity of various
polygon shapes. For shapes that are not rigid, they determine how to
make the shape more rigid.
- Students draw a geometric
representation and develop a formula to solve the problem of how many
handshakes will take place if there are n people and each
person shakes hands with each other person exactly once.
- Students work through the On the
Boardwalk lesson that is described in the Introduction to this
Framework. They determined the probability of winning a prize
when tossing a coin onto a grid by having the coin avoid all of the
grid lines.
- Students use graph models to represent a situation in which
a large company wishes to install a pneumatic tube system that would
enable small items to be sent between any of ten locales, possibly by
relay. Given the cost associated with possible tubes (edges), the
students work in groups to determine optimal pneumatic tube systems
for the company. They report their results in letters written
individually to the company president.
- Students work through the Making
Rectangles lesson that is described in the First Four Standards of
this Framework. They use combinations of algebra tiles which
they try to arrange into rectangle shapes to help them develop
procedures for multiplying binomials and factoring
polynomials.
25. Use inductive and deductive reasoning to solve
problems and to present reasonable explanations of and
justifications for the solutions.
- In a computer-based, open-ended, assessment, groups of
students use computer software to draw parallelograms, make
measurements, and list as many properties of parallelograms and their
diagonals as they can.
- Students prove deductively that a parallelogram
is divided into congruent triangle by a diagonal. They also prove
that any angle inscribed in a semi-circle is a right angle. (An angle
ABC is inscribed in a semi-circle if AC is a diameter and B is any
other point on the circle.)
- Students explain in writing to a friend what the formula is
for the measure of each interior angle in a regular polygon with
n sides and how it is derived.
- Students build staircases from cubes, recording the number
of steps and the total number of cubes used for each construction.
They look for patterns, expressing them in words and symbolically in
equations. They then try to justify their results using deductive
reasoning.
- Students use Cabri software to investigate what
happens when consecutive midpoints of a quadrilateral are connected in
order. They state a conjecture based on their investigation and
explain why they think it is true.
- Students investigate the relationship between the number
of diagonals that can be drawn from one vertex of a polygon and the
number of sides of that polygon. They write about their findings in
their journals.
- Students work through the A Sure Thing!?
lesson in the Introduction to this Framework. They investigate
the number of non-overlapping regions that can be created if they draw
all the chords joining n points on the circumference of a
circle.
26. Analyze patterns produced by processes of
geometric change and express them in terms of iteration,
approximation, limits, self-similarity, and fractals.
- Students duplicate the beginning stages of a fractal
construction in the plane and analyze the sequences of their
perimeters and their areas.
- Students use the reduction and enlargement capabilities of
a copy machine to investigate the effects on area. They make a table
showing the linear rate of reduction/enlargement and the resulting
area for each successive reduction/enlargement. Then they graph the
results - an exponential function showing either decay or
growth.
- Students use the slides and appropriate
activities from Fractals for the Classroom, Vol. 1 to analyze
patterns produced by changes in geometric shapes.
- Students model decay in a bacterial culture by cutting a
sheet of grid paper in half repeatedly and recording the area of each
rectangle in a table. They then graph the number of cuts versus the
area to see an example of exponential decay.
- Students plot the relationship between body height and arm
length for people from one year of age through adulthood on coordinate
grid paper and on log-log paper. They see that the graph is not a
straight line on the coordinate grid paper; it is actually a
logarithmic function. They find that the function appears as a
straight line on log-log paper.
27. Explore applications of other geometries in
real-world contexts.
|
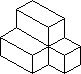
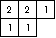



 Students are given a sheet with rectilinear figures (only right
angles) on it, such as the letter "E" at the right, and a
transparent square centimeter grid that they can place over each of
the figures. By counting the squares, they can find the area of each
figure; by counting the number of units around it, they can determine
its perimeter.
Students are given a sheet with rectilinear figures (only right
angles) on it, such as the letter "E" at the right, and a
transparent square centimeter grid that they can place over each of
the figures. By counting the squares, they can find the area of each
figure; by counting the number of units around it, they can determine
its perimeter.
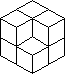



 Students use the "nibble" technique to create a shape
which will tessellate the plane, that is, copies of this shape will
fit together to cover a planar surface like a sheet of white oak-tag.
Start with a square, cut off a "nibble" along the top or
bottom edge of the square and
translate the nibble vertically to the opposite edge of the square;
the "nibble" will then be outside the boundary of the
original square. Take a "nibble" from the right or left
edge of the square and translate it horizontally to the opposite edge
of the square. Trace this shape repeatedly onto a sheet of white
oak-tag, by interlocking the pattern, and decorate the copies of the
shape. Attempt this process several times until a pleasing shape is
created.
Students use the "nibble" technique to create a shape
which will tessellate the plane, that is, copies of this shape will
fit together to cover a planar surface like a sheet of white oak-tag.
Start with a square, cut off a "nibble" along the top or
bottom edge of the square and
translate the nibble vertically to the opposite edge of the square;
the "nibble" will then be outside the boundary of the
original square. Take a "nibble" from the right or left
edge of the square and translate it horizontally to the opposite edge
of the square. Trace this shape repeatedly onto a sheet of white
oak-tag, by interlocking the pattern, and decorate the copies of the
shape. Attempt this process several times until a pleasing shape is
created.