STANDARD 11 - PATTERNS, RELATIONSHIPS, AND FUNCTIONS
|
All students will develop an understanding of patterns,
relationships, and functions and will use them to represent and
explain real-world phenomena.
|
Standard 11 - Patterns, Relationships, and Functions - Grades K-2
Overview
The development of pattern-based thinking, using patterns to
analyze and solve problems, is an extremely powerful tool for doing
mathematics, and leads in later grades to an appreciation of how
functions are used to describe relationships. The key components of
pattern-based thinking at the early grade levels, as identified
in the K-12 Overview, are recognizing, constructing, and extending
patterns, categorizing and classifying
objects, and discovering rules.
"Looking for patterns trains the mind to search out and
discover the similarities that bind seemingly unrelated information
together in a whole. . . . A child who expects things to 'make
sense' looks for the sense in things and from this
sense develops understanding. A child who does not see patterns often
does not expect things to make sense and sees all events as
discrete, separate, and unrelated."
- Mary Baratta-Lorton (cited on p.112 of About Teaching
Mathematics by Marilyn Burns)
Children in the primary grades develop an awareness of patterns in
their environment. Those who are successful in mathematics expand
this awareness into understanding and apply it to learning about the
number system. Children who do not look for patterns as a means of
understanding and learning mathematics often find mathematics to be
quite difficult. Thus, it is critical in the early grades to
establish an early predisposition to looking for patterns, creating
patterns, and extending patterns.
Children should recognize, construct and extend patterns
with pattern blocks, cubes, toothpicks, beans, buttons and other
concrete objects. Children in kindergarten can recognize patterns in
motion, color, designs, sound, rhythm, music, position, sizes, and
quantities. They are very aware of sound and rhythm, and can clap out
patterns that repeat, such as clapclapclappause, clapclapclappause,
etc. They can sit in a circle and wear colored hats which make a
pattern, such as redwhiteblue, redwhiteblue. One child can walk
around the circle and tap successive children in an armshoulderhead
pattern. The teacher may ask the class who the next person to be
tapped on the head would be if the pattern were to be continued. In
addition to repeating patterns, students should have experiences with
expanding patterns. They can indicate such a pattern by using motion:
skipjumpturn around, skipjumpjumpturn around, skipjumpjumpjumpturn
around, and so on. Songs are excellent examples of repetition of
melody or of words, as well as of rhythmic patterns. Children's
literature abounds with stories which rely on rhythm, rhyming,
repetition and sequencing. As students move on to first and second
grade, they should start to create their own patterns and develop
pictorial and symbolic representations of those patterns. The
transition will be from working with patterns using physical objects
to using pictures, letters, and geometric figures in two and three
dimensions, and then to using symbols, such as words and numbers, to
represent patterns.
Categorization and classification are also important skills
for students in the primary grades. Kindergartners should have
numerous opportunities to sort, classify, describe, and order
collections of many different types of objects. For example, students
might be asked to sort attribute shapes, buttons, or boxes into two
groups and explain why they sorted them as they did. This area offers
an excellent opportunity for students to verbalize their thought
processes and to integrate learning in mathematics and science as they
sort natural objects such as shells, rocks, or leaves.
Discovering a rule and inputoutput games are
two other settings in which primary children can enhance their work
and their skills with patterns. The children might be asked to solve
the mystery of the crackers as the teacher slowly and
deliberately gives every boy two crackers and every girl four crackers
one day during snack time. The inequity is addressed, of course, as
soon as the children solve the mystery by discovering the rule that
the teacher was using. On a different day, first graders can be told
that they may request between 3 and 5 crackers for snack. But then
each child is actually given two crackers less than his or her
request. Again, as soon as the children verbalize the relationship
between the request (input) and the portion allotted (output), they
receive the missing crackers.
Establishing the habit of looking for patterns is exceedingly
important in the primary grades. By studying patterns, young children
develop necessary tools to become better learners of mathematics as
well as better problem solvers. In addition, patterns help students
to appreciate the beauty of mathematics and to make connections within
mathematics and among mathematics and other subject areas.
Standard 11 - Patterns, Relationships, and Functions - Grades K-2
Indicators and Activities
The cumulative progress indicators for grade 4 appear below in
boldface type. Each indicator is followed by activities which
illustrate how it can be addressed in the classroom in kindergarten
and in grades 1 and 2.
Experiences will be such that all students in grades K-2:
1. Reproduce, extend, create, and describe
patterns and sequences using a variety of materials.
- Students make a collage with examples of
patterns in nature.
- Students create visual patterns with objects, colors, or
shapes using materials such as buttons, macaroni, pattern blocks,
links, cubes, attrilinks or attribute blocks, toothpicks, beans, or
teddy bear counters. They challenge other students to describe or
extend their patterns.
- Students sort objects such as leaves, buttons, animal
pictures, and blocks, using categories corresponding to
characteristics like number of holes, number of sides, shapes, or
thickness.
- One child walks around the outside of a circle and taps
successive children in a headshouldershoulderhead pattern. The
teacher asks who the next person to be tapped on the head would be if
the pattern were to be continued. The children sing and act out the
song, Head, shoulders, knees and toes.
- Students describe patterns made from circles, triangles,
and squares, and select the next shape in the pattern.
- Students make patterns with letters and extend the
sequence.
- As an assessment task, students use letters to translate
patterns they have created with objects - for example, RRBRRB for
a Unifix pattern of redredblueredredblue, or ABBCABBC for a shape
pattern of square - circle - circle - triangle - square - circle
-circle - triangle.
- Students connect the dots to make a picture by following a
number sequence, such as 2, 4, 6, 8, ... .
- Students create one more and one less
patterns.
- Students create patterns with the calculator. They enter
any number such as 10, and then add 1 for 10+1= = = ... . The
calculator will automatically repeat the function and display 11, 12,
13, 14, etc. Some calculators may need to have the pattern entered
twice: 10+1=+1= = = ... . Other calculators will need 1++10= = =
... . Students may repeatedly add or subtract any number.
- Students name things that come in pairs (or 4s or 5s):
eyes, ears, hands, arms, legs, mittens, shoes, bicycle wheels, etc.
They work in pairs to find how many people there are if there are 20
eyes.
- Students count by 2, 5, or 10 using counters or creating
color patterns with Unifix or Linker cubes; they repeat this using
skip counting on a number line.
- Students use skip counting or calculators to find multiples
of numbers and then color them on the hundreds chart. Linking cubes
or Unifix cubes can be used to build towers or trains with every other
cube or every third cube a certain color to illustrate, recognize, and
practice skip counting patterns.
- Students write their first name repeatedly on a 10x10 grid,
and then color the first letter of their name to create a pattern.
They discuss the patterns formed.
- Students identify the same pattern in a variety of
contexts. For example, blackwhite-blackwhite is like sitstandsitstand
and ABAB and updownupdown and straightcurvestraightcurve.
- Students identify patterns on a calendar using pictures or
numerals. For example, in November, even dates might be marked with a
snowflake, and odd dates with a picture of a turkey. Or, they might
mark each date with the day of the week.
- Students create a pattern using various rubber stamp blocks
or picture designs.
- Students use or create patterns with geometric figures
(circles, triangles, squares, pentagons, hexagons, etc.) and record
how many of each shape exist after each repeating cluster.
- Students create a mosaic design (tessellation) made of
different shapes using objects such as pattern blocks. They color
congruent shapes of a mosaic design with the same color.
2. Use tables, rules, variables, open sentences, and
graphs to describe patterns and other relationships.
- Students complete a table given several starting numbers
and a verbal rule.
- Kindergartners look at Anno's
Counting House by Mitsumasa Anno to see if they can figure out the
pattern that is used in moving from one set of pages to the next. The
people in this book move, one by one, from one house to
another.
- Students describe the pattern illustrated by the numbers
in a table by using words (e.g., one more than), and then the teacher
helps them to represent it with symbols in an open sentence
(
 = =  + 1). + 1).
- Students use colored squares to make a graph showing
the multiples of 3 and relate this to a table and an expression
involving a variable, such as 3 x
 . .
3. Use concrete and pictorial models to explore
the basic concept of a function.
- Students study the
pictures in Anno's Math Games II by Mitsumasa Anno.
As they do, they try to figure out what happens to the objects as the
elves put them into the magic machine. Sometimes the number of
objects doubles, sometimes the objects grow eyes, and sometimes the
objects turn into circles.
- Students put numbers into Max the Magic Math Machine
and read what comes out. (The teacher acts as Max.) Then they
describe what Max is doing to each number. The teacher pays careful
attention to the students' responses to assess their levels of
understanding.
- Students investigate a hole-making machine that puts 4
holes into buttons. They make a table that shows the number of
buttons put into the machine and the total number of holes that must
be made in them. Then they write a sentence that describes how the
total number of holes changes as new buttons are added.
- Students play Guess my Rule. The teacher gives them
a starting number and the result after using the rule. She continues
giving examples until students discover the rule.
- Students count the number of pennies (or nickels) in 1
dime, 2 dimes, 3 dimes and record their results in chart form. They
study the patterns and discuss the rules observed.
- Students consider the cost of two or three candies if one
candy costs one dime. They make a chart using the information.
- Students count the number of lifesavers in an assorted
pack. They make a table showing the number of each color and the
total number in one pack. Then, assuming all of the packs are the
same, they make a table showing the total number of each color for 2
packs, 3 packs, 4 packs, and so on. They check their results with
packs of lifesavers, which in general, have the same number of each
color.
4. Observe and explain how a change in one
physical quantity can produce a corresponding change in
another.
- Students discuss how ice changes to water as it warms.
They talk about how it snows in January or February but rains in April
or May.
- Students plant seeds and watch them grow. They write
about what they see and measure the height of their plants as time
passes. They discuss how changes in time bring about changes in the
height of the plants. They also talk about how other factors might
affect the plants, such as light and water.
5. Observe and recognize examples of patterns,
relationships, and functions in other disciplines and
contexts.
- Students go on a pattern hunt around the classroom
and the school, discussing the patterns they find.
- Students sing and act out songs like "Rattlin'
Bog" (Bird on the leaf, and the leaf on the tree, and the tree
in the hole, and the hole in the ground, . . .) and "Old
MacDonald Had a Farm."
- In reading, students recognize patterns in rhythm, in
rhyming, in syllables and in sequencing. Stories such as Ten Black
Dots by Donald Crews, Five Little Monkeys Jumping on a
Bed by Eileen Christelow, Jump, Frog, Jump by Robert Kalan,
The Little Red Hen, and Dr. Seuss books offer such
opportunities. Visual patterns can be shown using picture
representations for children's books such as 1 Hunter by
Pat Hutchins, Rooster's Off to See the World by
Eric Carle, The Patchwork Quilt by Valerie Flournoy, and The
Keeping Quilt by Patricia Polacco.
- Students identify every third letter of the alphabet; every
fourth letter, etc. They use those sets of letters to see what words
they can make.
- Students choose a day. Using a calendar, they identify the
name of the next day, of theprevious day, and also the name of the day
two days (or more) before and after. They select a date, and give the
date of the next day and of the previous day, the name of the month,
of the next month, and of the previous month. They give the name of
the date two days before and after, and three days (or more) before
and after.
- Students graph daily weather patterns, showing sunny,
cloudy, rainy or snowy days. Then they discuss monthly or seasonal
patterns.
- In social studies, students identify traffic patterns such
as how many cars, trucks, or buses pass the front of the school during
five minutes at different times of the day. They keep records for
five days, organizing the information in chart form.
- In art, students observe patterns in pictures, mosaics,
tessellations, and Escherlike drawings, as well as in wallpaper,
fabric, and floor tile designs.
6. Form and verify generalizations based on
observations of patterns and relationships.
- Students draw pictures of faces and make a table that shows
the number of faces and the number of eyes. The teacher writes a
sentence on the board that the class composes, describing the patterns
that they find.
- Students observe that there are 12 eggs in a carton of
eggs. These are called a dozen. They explain how to find the number
of eggs in 2 cartons, 3 cartons, and so on.
- Students write a sentence or more telling about the
patterns they have observed in a particular activity. They may use
pictures to describe or generalize what they have observed. For
example, after students have colored multiples of a certain number on
the hundreds chart, they write about the geometric pattern they
observe on the chart.
References
-
Anno, Mitsumasa. Anno's Counting House. New
York: Philomel Books, 1982.
Anno, Mitsumasa. Anno's Math Games II. New
York: Philomel Books, 1982.
Burns, Marilyn. About Teaching Mathematics: A K-8
Resource. Sausalito, CA: Math Solutions Publications,
1992.
Carle, Eric. Rooster's Off to See the World.
New York: Simon & Schuster Books for Young Readers, 1972.
Christelow, Eileen. Five Little Monkeys Jumping on a Bed.
New York: Clarion Books, 1989.
Crews, Donald. Ten Black Dots. New York: Greenwillow
Books, 1986.
Flournoy, Valerie. The Patchwork Quilt. New York: Dial
Books, 1985.
Hutchins, Pat. 1 Hunter. New York: Greenwillow Books,
1982.
Kalan, Robert. Jump, Frog, Jump. New York: Greenwillow
Books, 1981.
Polacco, Patricia. The Keeping Quilt. New York: Simon
and Schuster, 1988.
Seuss, Dr. Most Dr. Seuss books exhibit appropriate
patterns.
The Little Red Hen. Many versions are available.
On-Line Resources
-
http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/
The Framework will be available at this site during
Spring 1997. In time, we hope to post additional resources
relating to this standard, such as grade-specific activities submitted
by New Jersey teachers, and to provide a forum to discuss the
Mathematics Standards.
|
 =
= 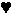 + 1).
+ 1).