STANDARD 14 - DISCRETE MATHEMATICS
|
All students will apply the concepts and methods of discrete
mathematics to model and explore a variety of practical
situations.
|
Standard 14 - Discrete Mathematics - Grades 5-6
Overview
The five major themes of discrete mathematics, as discussed in the
K-12 Overview, are systematic listing, counting, and
reasoning; discrete mathematical modeling using graphs (networks) and
trees; iterative (that is, repetitive) patterns and processes;
organizing and processing information; and following and
devising lists of instructions, called
"algorithms," and using them to find the best
solution to real-world problems. Two important resources
on discrete mathematics for teachers at all levels are the 1991 NCTM
Yearbook Discrete Mathematics Across the Curriculum K-12 and
the 1997 DIMACS Volume Discrete Mathematics in the Schools: Making
an Impact.
Despite their formidable titles, these five themes can be addressed
with activities at the 5-6 grade level which involve both the
purposeful play and simple analysis suggested for elementary school
students and experimentation and abstraction appropriate at the middle
grades. Indeed, teachers will discover that many activities that they
already are using in their classrooms reflect these themes. These
five themes are discussed in the paragraphs below.
The following discussion of activities at the 5-6 grade levels
in discrete mathematics presupposes that corresponding
activities have taken place at the K-4 grade levels. Hence 5-6 grade
teachers should review the K-2 and 3-4 grade level discussions
of discrete mathematics and might use activities similar to those
described there before introducing the activities for this
grade level.
Activities involving systematic listing, counting, and
reasoning at K-4 grade levels can be extended to the 5-6 grade
level. For example, they might determine the number of possible
license plates with two letters followed by three numbers followed by
one letter, and decide whether this total number of license plates is
adequate for all New Jersey drivers. They need to become familiar
with the idea of permutations, that is, the different ways in
which a group of items can be arranged. Thus, for example, if three
children are standing by the blackboard, there are altogether six
different ways, call permutations, in which this can be done; for
example, if the three children are Amy (A), Bethany (B), and Coriander
(C), the six different permutations can be described as ABC, ACB, BAC,
BCA, CAB, and CBA. Similarly, the total number of different ways in
which three students out of a class of thirty can be arranged at the
blackboard is altogether 30x29x28, or 24,360 ways, an amazing
total!
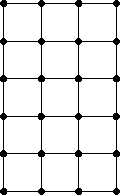 An important discrete mathematical model is that of a
network or graph, which consists of dots and lines
joining the dots; the dots are often called vertices (vertex is
the singular) and the lines are often called edges. (This is
different from other mathematical uses of the term "graph";
the two terms "network" and "graph" are used
interchangeably for this concept.) An example of a graph with 24
vertices and 38 edges is given at the left. Graphs can be used to
represent islands and bridges, or buildings and roads, or houses and
telephone cables; wherever a collection of things are joined by
connectors, the mathematical model used is that of a graph. At the
5-6 level, students should be familiar with thenotion of a graph and
recognize situations in which graphs can be an appropriate model. For
example, they should be familiar with problems involving routes for
garbage pick-ups, school buses, mail deliveries, snow removal, etc.;
they should be able to model such problems by using graphs, and be
able to solve such problems by finding suitable paths in these graphs,
such as in the town whose street map is the graph above.
An important discrete mathematical model is that of a
network or graph, which consists of dots and lines
joining the dots; the dots are often called vertices (vertex is
the singular) and the lines are often called edges. (This is
different from other mathematical uses of the term "graph";
the two terms "network" and "graph" are used
interchangeably for this concept.) An example of a graph with 24
vertices and 38 edges is given at the left. Graphs can be used to
represent islands and bridges, or buildings and roads, or houses and
telephone cables; wherever a collection of things are joined by
connectors, the mathematical model used is that of a graph. At the
5-6 level, students should be familiar with thenotion of a graph and
recognize situations in which graphs can be an appropriate model. For
example, they should be familiar with problems involving routes for
garbage pick-ups, school buses, mail deliveries, snow removal, etc.;
they should be able to model such problems by using graphs, and be
able to solve such problems by finding suitable paths in these graphs,
such as in the town whose street map is the graph above.
Students should recognize and work with repetitive patterns and
processes involving numbers and shapes, with objects found in the
classroom and in the world around them. Building on these
explorations, fifth- and sixth-graders should also recognize and work
with iterative and recursive processes. They explore iteration
using Logo software, where they recreate a variety of interesting
patterns (such as a checkerboard) by iterating the construction of a
simple component of the pattern (in this case a square). As with
younger students, 5th and 6th graders are fascinated with the
Fibonacci sequence 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... where
every number is the sum of the previous two numbers. Although the
Fibonacci sequence starts with small numbers, the numbers in the
sequence become large very quickly. Students can now also begin to
understand the Fibonacci sequence and other sequences recursively
- where each term of the sequence is described in terms of
preceding terms.
Students in the 5th and 6th grade should investigate sorting
items using Venn diagrams, and continue their explorations
of recovering hidden information by decoding messages. They
should begin to explore how codes are used to communicate
information, by traditional methods such as Morse code or
semaphore (flags used for ship-to-ship messages) and also by current
methods such as zip codes, which describe a location in the United
States by a five-digit (or nine-digit) number. Students should also
explore modular arithmetic through applications involving clocks,
calendars, and binary codes.
Finally, at grades 5-6, students should be able to describe,
devise, and test algorithms for solving a variety of
problems. These include finding the shortest route from one
location to another, dividing a cake fairly, planning a tournament
schedule, and planning layouts for a class newspaper.
Two important resources on discrete mathematics for teachers at all
levels is the 1991 NCTM Yearbook Discrete Mathematics Across the
Curriculum K-12 and the 1997 DIMACS Volume Discrete Mathematics
in the Schools: Making An Impact. Another important
resource for 5-6 teachers is This Is MEGA-Mathematics!
Standard 14 - Discrete Mathematics - Grades 5-6
Indicators and Activities
The cumulative progress indicators for grade 8 appear below in
boldface type. Each indicator is followed by activities which
illustrate how it can be addressed in the classroom in grades 5 and
6.
Building upon knowledge and skills gained in the preceding grades,
experiences will be such that all students in grades 5-6:
6. Use systematic listing, counting, and
reasoning in a variety of different contexts.
- Students determine the number of different sandwiches or
hamburgers that can be created at local eateries using a combination
of specific ingredients.
- Students find the number of different ways to
make a row of flowers each of which is red or yellow, if the row has
1, 2, 3, 4, or 5 flowers. Modeling this with Unifix cubes, they
discover that adding an additional flower to the row doubles the
number of possible rows, provide explanations for this, and generalize
to longer rows. Similar activities can be found in the Pizza
Possibilities and Two-Toned Towers lessons that are
described in the First Four Standards of this
Framework.
- Students find the number of ways of asking three different
students in the class to write three homework problems on the
blackboard.
- Students understand and use the concept of permutation.
They determine the number of ways any five items can be arranged in
order, justify their conclusion using a tree diagram, and use
factorial notation, 5!, to summarize the result.
- Students find the number of possible telephone numbers with
a given area code and investigate why several years ago the telephone
company introduced a new area code (908) in New Jersey, and why
additional area codes are being introduced in 1997. Is the
situation the same with zip codes?
- Students estimate and then calculate the number
of possible license plates with two letters followed by three numbers
followed by one letter. They investigate why the state license bureau
tried to introduce license plates with seven characters and why this
attempt might have been unsuccessful.
- Students explore the sequence of triangular
numbers 1, 1 + 2, 1 + 2 + 3, 1 + 2 + 3 + 4, ... which represent the
number of dots in the triangular arrays below, and find the location
of the triangular numbers in Pascal's triangle.

- Students look for patterns in the various diagonals of
Pascal's triangle, and in the differences between consecutive
terms in these diagonals. Patterns in Pascal's
Triangle Poster is a nice resource for introducing these
ideas.
- Students analyze simple games like the following: Beth
wins the game whenever the two dice give an even total, and Hobart
wins whenever the two dice give an odd total. They play the game a
number of times, and using experimental evidence, decide whether the
game is fair, and, if not, which player is more likely to win. They
then try to justify their conclusions theoretically, by counting the
number of combinations of dice that would result in a win for each
player.
- Students create a table in the form of a grid which
indicates how many of each of the coins of the fictitious country
"Ternamy" - in denominations of 1, 3, 9, 27, and 81
"terns" - are needed to make up any amount from 1 to
200. They list the denominations in the columns at the top of the
table and the amounts they are trying to make in the rows at the left.
They write the number of each coin needed to add up to the desired
amount in the appropriate squares in that row. The only
"rule" to be followed is that the least number of coins must
be used; for example, three 1's should always be replaced by one 3.
This table can be used to introduce base 3 ("ternary")
numbers, and then numbers in other bases.
7. Recognize common discrete mathematical models, explore
their properties, and design them for specific
situations.
- Students experiment with drawing make-believe
maps which can be colored with two, three, and four colors (where
adjacent countries must have different colors), and explain why their
fictitious maps, and real maps like the map of the 50 states, cannot
be colored with fewer colors. Note that it was proven in 1976 that no
map can be drawn on a flat surface which requires more than four
colors. The Mathematician's Coloring Book contains
a variety of map-coloring activities, as well as historical background
on the map coloring problem.
- Students play games using graphs. For example,
in the strolling game, two players stroll together on a path through
the graph which never repeats itself; they alternate in selecting
edges for the path, and the winner is the one who selects the last
edge on the path. Who wins? In the game below, Charles
and Diane both start at V, Charles picks the first edge (marked 1) and
they both stroll down that edge. Then Diane picks the second edge
(marked 2) and the game continues. Diane has won this play of the
game since the path cannot be continued after the sixth edge without
repeating itself. Does Diane have a way of always winning
this game, or does Charles have a winning strategy? What if there was
a different starting point? What if a different graph was
used? What if the path must not cross itself (instead of
requiring that it not repeat itself)? Students should try to
explain in each case why a certain player has a winning
strategy.

- Students find paths in graphs which utilize each edge
exactly once; a path in a graph is asequence of edges each of which
begins where the previous one ends. They apply this idea by
converting a street map to a graph where vertices on the graph
correspond to intersections on the street map, and by using this graph
to determine whether a garbage truck can complete its sector without
repeating any streets. See the segment Snowbound: Euler
Circuits on the videotape Geometry: New Tools for New
Technologies; the module Drawing Pictures With One Line
provides a strong background for problems of this kind.
- Students plan emergency evacuation routes at school or from
home using graphs.
- All of the students together create a
"human graph" where each child in the class is holding two
strings, one in each hand. This can be accomplished by placing in the
center of the room a number of pieces of yarn (each six feet long)
equal to the number of students, and having each student take the ends
of two strings. The children are asked to untangle themselves, and
discuss or write about what happens.
- Students play the game of Sprouts, in which two
students take turns in building a graph until one of them (the
winner!) completes the graph. The rules are: start the game with two
or three vertices; each person adds an edge (it can be a curved line!)
joining two vertices, and then adds a new vertex at the center of that
edge; no more than three edges can occur at a vertex; edges may not
cross. In the sample game below, the second player (B) wins because
the first player (A) cannot draw an edge connecting the only two
vertices that have degree less than three without crossing an existing
edge.

8. Experiment with iterative and recursive processes,
with the aid of calculators and computers.
- Students develop a method for solving the Tower of Hanoi
problem: There are three pegs, on the first of which is stacked five
disks, each smaller than the ones underneath it (see diagram below);
the problem is to move the entire stack to the third peg, moving
disks, one at a time, from any peg to either of the other two pegs,
with no disk ever placed upon a smaller one. How many moves are
required to do this?
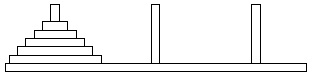
- Students use iteration in Logo software to draw
checkerboards, stars, and other designs. For example, they iterate the
construction of a simple component of a pattern, such as a square, to
recreate an entire checkerboard design.
- Students use paper rabbits (prepared by the teacher) with
which to simulate Fibonacci's 13th century investigation into the
growth of rabbit populations: If you start with one pairof
baby rabbits, how many pairs of rabbits will there be a year
later? Fibonacci's assumption was that each pair of baby
rabbits results in another pair of baby rabbits two months later
- allowing a month for maturation and a month for gestation.
Once mature, each pair has baby rabbits monthly. (Each pair of
students should be provided with 18 cardboard pairs each of baby
rabbits, not-yet-mature rabbits, and mature rabbits.) The
Fascinating Fibonaccis by Trudi Garland illustrates the
rabbit problem and a number of other interesting Fibonacci facts. In
Mathematics Mystery Tour by Mark Wahl, an elementary school
teacher provides a year's worth of Fibonacci explorations and
activities.
- Students use calculators to compare the growth
of various sequences, including counting by 4's (4, 8, 12, 16, ... ),
doubling (1, 2, 4, 8, 16, ... ), squaring (1, 4, 9, 16, 25, ... ), and
Fibonacci (1, 1, 2, 3, 5, 8, 13, ... ).
- Students explore their surroundings to find rectangular
objects whose ratio of length to width is the "golden
ratio." Since the golden ratio can be approximated by the ratio
of two successive Fibonacci numbers, students should cut a rectangular
peephole of dimensions 21mm x 34 mm out of a piece of cardboard, and
use it to "frame" potential objects; when it
"fits," the object is a golden rectangle. They describe
these activities in their math journals.
- Students study the patterns of patchwork quilts, and make
one of their own. They might first read Eight Hands Round.
- Students make equilateral triangles whose sides are
9", 3", and 1" (or other lengths in ratio 3:1), and use
them to construct "Koch snowflakes of stage 2" (as shown
below) by pasting the 9" triangle on a large sheet of paper,
three 3" triangles at the middle of the three sides of the
9" triangle (pointing outward), and twelve 1" triangles at
the middle of the exposed sides of the twelve 3" segments
(pointing outward). To get Koch snowflakes of stage 3, add
forty-eight 1/3" equilateral triangles. How many 1/9"
equilateral triangles would be needed for the Koch snowflake of
stage 4? Fractals for the Classroom is a valuable resource
for these kinds of activities and explorations.
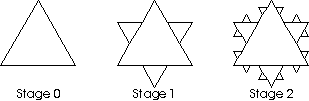
- Students mark one end of a long string and make another
mark midway between the two ends. They then continue marking the
string by following some simple rule such as "make a new mark
midway between the last midway mark and the marked end" and then
repeat this instruction. Students investigate the relationship of the
lengths of the segments between marks. How many marks are possible
in this process if it is assumed that the marks take up no
space on the string? What happens if the rule is changed to
"make a new mark midway between the last two
marks?"
9. Explore methods for storing, processing, and
communicating information.
- After discussing possible methods for communicating
messages across a football field, teams of students devise methods for
transmitting a short message (using flags, flashlights, arm signals,
etc.). Each team receives a message of the same length and must
transmit it to members of the team at the other end of the field as
quickly and accurately as possible.
- Students devise rules so that arithmetic expressions
without parentheses, such as 5 x 8 - 2 / 7, can be
evaluated unambiguously. They then experiment with calculators to
discover the calculators' built-in rules for evaluating these
expressions.
- Students explore binary arithmetic and arithmetic for other
bases through applications involving clocks (base 12), days of the
week (base 7), and binary (base 2) codes.
- Students assign each letter in the alphabet a numerical
value (possibly negative) and then look for words worth a specified
number of points.
- Students send and decode messages in which letters of the
message are systematically replaced by other letters. The Secret
Code Book by Helen Huckle shows these coding systems as well as
others.
-
 Students use Venn diagrams to sort and then report on
their findings in a survey. For example, they can seek responses to
the question, When I grow up I want to be a) rich and
famous, b) a parent, c) in a profession I love, where
respondents can choose more than one option. The results can be
sorted into a Venn diagram like that at the right, where entries
"m" and "f" are used for male and female
students. The class can then determine answers to questions like
Are males or females in our class more likely to have a single
focus? Tabletop, Jr. software can be used to sort and
explore data using Venn diagrams.
Students use Venn diagrams to sort and then report on
their findings in a survey. For example, they can seek responses to
the question, When I grow up I want to be a) rich and
famous, b) a parent, c) in a profession I love, where
respondents can choose more than one option. The results can be
sorted into a Venn diagram like that at the right, where entries
"m" and "f" are used for male and female
students. The class can then determine answers to questions like
Are males or females in our class more likely to have a single
focus? Tabletop, Jr. software can be used to sort and
explore data using Venn diagrams.
10. Devise, describe, and test algorithms for
solving optimization and search problems.
- Students use a systematic procedure to find the total
number of routes from one location in their town to another, and the
shortest such route. (See Problem Solving Using Graphs.)
- In Turtle Math, students use Logo
commands to go on a treasure hunt, and look for the shortest route to
complete the search.
- Students discuss and write about various methods of
dividing a cake fairly, such as the "divider/chooser method"
for two people (one person divides, the other chooses) and the
"lone chooser method" for three people (two people divide
the cake using the divider/chooser method, then each cuts his/her half
into thirds, and then the third person takes one piece from each of
the others). Fair Division: Getting Your Fair Share can be
used to explore methods of fairly dividing a cake or an estate.
- Students conduct a class survey for the top ten songs and
discuss different ways to use the information to select the
winners.
- Students devise a telephone tree for disseminating messages
to all 6th grade students and their parents.
- Students schedule the matches of a volleyball tournament in
which each team plays each other team once.
- Students use flowcharts to represent visually the
instructions for carrying out a complex project, such as scheduling
the production of the class newspaper.
- Students develop an algorithm to create an efficient layout
for a class newspaper.
References
-
Bennett, S., et al. Fair Division: Getting Your Fair
Share. Consortium for Mathematics and Its Applications
(COMAP). Module #9, 1987.
Casey, Nancy, and Mike Fellows. This is MEGA-Mathematics!
- Stories and Activities for
Mathematical Thinking, Problem-Solving, and Communication.
Los Alamos, CA: Los Alamos National Laboratories, 1993. (A
version is available online at
http://www.c3.lanl.gov/mega-math)
Chavey, D. Drawing Pictures With One Line. Consortium
for Mathematics and Its Applications (COMAP). Module #21,
1992.
Cozzens, M., and R. Porter. Problem Solving Using Graphs.
Consortium for Mathematics and Its Applications (COMAP). Module
#6, 1987.
Francis, R. The Mathematician's Coloring
Book. Consortium for Mathematics and Its Applications
(COMAP). Module #13.
Garland, Trudi. The Fascinating Fibonaccis. Palo Alto,
CA: Dale Seymor Publications, 1987.
Huckle, Helen. The Secret Code Book. Dial Books.
Kenney, M. J., Ed. Discrete Mathematics Across the Curriculum
K-12. 1991 Yearbook of the National Council of Teachers of
Mathematics (NCTM). Reston, VA, 1991.
Paul, A. Eight Hands Round. New York: Harper Collins,
1991.
Peitgen, Heinz-Otto, et al. Fractals for the Classroom:
Strategic Activities Volume One & Two. Reston, VA: NCTM and
New York: Springer- Verlag, 1992.
Rosenstein, J. G., D. Franzblau, and F. Roberts, Eds.
Discrete Mathematics in the Schools:
Making an Impact. Proceedings of a 1992 DIMACS Conference
on "Discrete Mathematics in the Schools." DIMACS Series
on Discrete Mathematics and Theoretical Computer Science.
Providence, RI: American Mathematical Society (AMS), 1997.
(Available online from this chapter in
http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/.)
Wahl, Mark. Mathematical Mystery Tour: Higher-Thinking Math
Tasks. Tucson, AZ: Zephyr Press, 1988.
Software
-
Logo. Many versions of Logo are commercially
available.
Tabletop, Jr. Broderbund, TERC.
Turtle Math. LCSI.
Video
-
Geometry: New Tools for New Technologies, videotape by
the Consortium for Mathematics and Its Applications (COMAP).
Lexington, MA, 1992.
On-Line Resources
-
http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/
The Framework will be available at this site during
Spring 1997. In time, we hope to post additional resources
relating to this standard, such as grade-specific activities submitted
by New Jersey teachers, and to provide a forum to discuss the
Mathematics Standards.
|
 An important discrete mathematical model is that of a
network or graph, which consists of dots and lines
joining the dots; the dots are often called vertices (vertex is
the singular) and the lines are often called edges. (This is
different from other mathematical uses of the term "graph";
the two terms "network" and "graph" are used
interchangeably for this concept.) An example of a graph with 24
vertices and 38 edges is given at the left. Graphs can be used to
represent islands and bridges, or buildings and roads, or houses and
telephone cables; wherever a collection of things are joined by
connectors, the mathematical model used is that of a graph. At the
5-6 level, students should be familiar with thenotion of a graph and
recognize situations in which graphs can be an appropriate model. For
example, they should be familiar with problems involving routes for
garbage pick-ups, school buses, mail deliveries, snow removal, etc.;
they should be able to model such problems by using graphs, and be
able to solve such problems by finding suitable paths in these graphs,
such as in the town whose street map is the graph above.
An important discrete mathematical model is that of a
network or graph, which consists of dots and lines
joining the dots; the dots are often called vertices (vertex is
the singular) and the lines are often called edges. (This is
different from other mathematical uses of the term "graph";
the two terms "network" and "graph" are used
interchangeably for this concept.) An example of a graph with 24
vertices and 38 edges is given at the left. Graphs can be used to
represent islands and bridges, or buildings and roads, or houses and
telephone cables; wherever a collection of things are joined by
connectors, the mathematical model used is that of a graph. At the
5-6 level, students should be familiar with thenotion of a graph and
recognize situations in which graphs can be an appropriate model. For
example, they should be familiar with problems involving routes for
garbage pick-ups, school buses, mail deliveries, snow removal, etc.;
they should be able to model such problems by using graphs, and be
able to solve such problems by finding suitable paths in these graphs,
such as in the town whose street map is the graph above.




 Students use Venn diagrams to sort and then report on
their findings in a survey. For example, they can seek responses to
the question, When I grow up I want to be a) rich and
famous, b) a parent, c) in a profession I love, where
respondents can choose more than one option. The results can be
sorted into a Venn diagram like that at the right, where entries
"m" and "f" are used for male and female
students. The class can then determine answers to questions like
Are males or females in our class more likely to have a single
focus? Tabletop, Jr. software can be used to sort and
explore data using Venn diagrams.
Students use Venn diagrams to sort and then report on
their findings in a survey. For example, they can seek responses to
the question, When I grow up I want to be a) rich and
famous, b) a parent, c) in a profession I love, where
respondents can choose more than one option. The results can be
sorted into a Venn diagram like that at the right, where entries
"m" and "f" are used for male and female
students. The class can then determine answers to questions like
Are males or females in our class more likely to have a single
focus? Tabletop, Jr. software can be used to sort and
explore data using Venn diagrams.