The five major themes of discrete mathematics, as discussed in the K-12 Overview, are systematic listing, counting, and reasoning; discrete mathematical modeling using graphs (networks) and trees; iterative (that is, repetitive) patterns and processes; organizing and processing information; and following and devising lists of instructions, called "algorithms," and using them to find the best solution to real-world problems.

The following discussion of activities at the 9-12 grade levels in discrete mathematics presupposes that corresponding activities have taken place at the K-8 grade levels. Hence high school teachers should review the discussions of discrete mathematics at earlier grade levels and might use activities similar to those described there before introducing the activities for these grade levels.

At the high school level, students are becoming familiar with algebraic and functional notation, and their understanding of all of the themes of discrete mathematics and their ability to generalize earlier activities should be enhanced by their algebraic skills and understandings. Thus, for example, they should use formulas to express the results of problems involving permutations and combinations, relate Pascal's triangle to the coefficients of the binomial expansion of (x+y)ⁿ, explore models of growth using various algebraic models, explore iterations of functions, and discuss methods for dividing an estate among several heirs.

At the high school level, students are particularly interested in applications; they ask What is all of this good for? In all five areas of discrete mathematics, students should focus on how discrete mathematics is used to solve practical problems. Thus, for example, they should be able to apply their understanding of counting techniques, to analyze lotteries; of graph coloring, to schedule traffic lights at a local intersection; of paths in graphs, to devise patrol routes for police cars; of iterative processes, to analyze and predict fish populations in a pond or concentration of medicine in the bloodstream; of codes, to understand how bar-code scanners detect errors and how CD's correct errors; and of optimization, to understand the 200 year old debates about apportionment and to find efficient ways of scheduling the components of a complex project.

Two important resources on discrete mathematics for teachers at all grade levels are the 1991 NCTM Yearbook, Discrete Mathematics Across the Curriculum K-12 and the DIMACS Volume, Discrete Mathematics in the Schools: Making an Impact edited by J. Rosenstein, D. Franzblau, and F. Roberts. Useful resources at the high school level are Discrete Mathematics Through Applications by N. Crisler, P. Fisher, and G. Froelich; For All Practical Purposes: Introduction to Contemporary Mathematics, by the Consortium for Mathematics and its Applications; and Excursions in Modern Mathematics by P. Tannenbaum and R. Arnold.

The cumulative progress indicators for grade 12 appear below in boldface type. Each indicator is followed by activities which illustrate how it can be addressed in the classroom in grades 9, 10, 11, and 12.

Building upon knowledge and skills gained in the preceding grades, experiences will be such that all students in grades 9-12:

11. Understand the basic principles of iteration, recursion, and mathematical induction.

• Students relate the possible outcomes of tossing five coins with the binomial expansion of (x+y)⁵ and the fifth row of Pascal's triangle, and generalize to values of n other than 5.

• Students develop formulas for counting paths on grids or other simple street maps.

• Students find the number of cuts needed in order to divide a giant pizza so that each student in the school gets at least one piece.

• Students develop a precise description, using iteration, of the standard algorithm for adding two integers.

12. Use basic principles to solve combinatorial and algorithmic problems.

• Students determine the number of ways of spelling "mathematics" in the array below by following a path from top to bottom in which each letter is directly below, and just to the right or left of the previous letter.

  					M
  				A		A
  			T		T		T
  		H		H		H		H
  	E		E		E		E		E
  M		M		M		M		M		M
  	A		A		A		A		A
  		T		T		T		T
  			I		I		I
  				C		C
  					S

• Students determine the number of ways a committee of three members could be selected from the class, and the number of ways three people with specified roles could be selected. They generalize this activity to finding a formula for the number of ways an n person committee can be selected from a class of m people, and the number of ways n people with specified roles can be selected from a class of m people.

• Students find the number of ways of lining up thirty students in a class, and compare that to other large numbers; for example, they might compare it to the number of raindrops (volume = .1 cc) it would take to fill a sphere the size of the earth (radius = 6507 KM).

• Students determine the number of ways of dividing 52 cards among four players, as in the game of bridge, and compare the number of ways of obtaining a flush (five cards of the same suit) and a full house (three cards of one denomination and two cards of another) in the game of poker.

• Students play Nim (and similar games) and discuss winning strategies using binary representations of numbers.

13. Use discrete models to represent and solve problems.

• Students study the four color theorem and its history. (The Mathematicians' Coloring Book provides a good background for coloring problems.)

• Students using graph coloring to determine the minimum number of guards (or cameras) needed for museums of various shapes (and similarly for placement of lawn sprinklers or motionsensor burglar alarms).

• Students use directed graphs to represent tournaments (where an arrow drawn from A to B represents "A defeats B") and food webs (where an arrow drawn from A to B represents "A eats B"), and to construct oneway orientations of streets in a given town which involve the least inconvenience to drivers. (A directed graph is simply a graph where each edge is thought of as an arrow pointing from one endpoint to the other.)

• Students use tree diagrams to analyze the play of games such as tic-tac-toe or Nim, and to represent the solutions to weighing problems. Example: Given 12 coins one of which is "bad," find the bad one, and determine whether it is heavier or lighter than the others, using three weighings.

• Students use graph coloring to schedule the school's final examinations so that no student has a conflict, if at all possible, or to schedule traffic lights at an intersection.

• Students devise graphs for which there is a path that covers each edge of the graph exactly once, and other graphs which have no such paths, based on an understanding of necessary and sufficient conditions for the existence of such paths, called "Euler paths," in a graph. Drawing Pictures With One Line provides background and applications for Euler path problems.

• Students make models of polyhedra with straws and string, and explore the relationship between the numbers of edges, faces, and vertices, and generalize the conclusion to planar graphs.

• Students use graphs to solve problems like the "fire-station problem": Given a city where the streets are laid out in a grid composed of many square blocks, how many fire stations are needed to provide adequate coverage of the city if each fire station services its square block and the four square blocks adjacent to that one? The Maryland Science Center in Baltimore has a hands-on exhibit involving a fire-station problem for 35 square blocks arranged in a six-by-six grid with one corner designated a park.

14. Analyze iterative processes with the aid of calculators and computers.

• Students analyze the Fibonacci sequence 1, 1, 2, 3, 5, 8, 13, 21, ... as a recurrence relation A _{n + 2} = A_n + A_{n + 1} with connections to the golden ratio. Fascinating Fibonaccis illustrates a variety of connections between Fibonacci numbers and the golden ratio.

• Students solve problems involving compound interest using iteration on a calculator or on a spreadsheet.

• Students explore examples of linear growth, using the recursive model based on the formula A_n+1 = A_n + d, where d is the common difference, and convert it to the explicit linear formula, A_n+1 = A₁ + n × d.

• Students explore examples of population growth, using the recursive model based on the formula A_n+1 = A_n x r, where r is the common multiple or growth rate, convert it to the explicit exponential formula A_n+1 = A₁ rⁿ, and apply it to both economics (such as interest problems) and biology (such as concentration of medicine in blood supply).

• Students explore logistic growth models of population growth, using the recursive model based on the formula A_n+1 = A_n x (1 - A_n) x r, where r is the growth rate and A_n is the fraction of the carrying capacity of the environment, and apply this to the population of fish in a pond. Using a spreadsheet, students experiment with various values of the initial value A₁ and of the growth rate, and describe the relationship between the values chosen and the long term behavior of the population.

• Students explore the pattern resulting from repeatedly multiplying 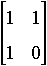by itself.

• Students use a calculator or a computer to study simple Markov chains, such as weather prediction and population growth models. (See Chapter 7.3 of Discrete Mathematics Through Applications.)

• Students explore graphical iteration by choosing a function key on a calculator and pressing it repeatedly, after choosing an initial number, to get sequences of numbers like 2, 4, 8, 16, 32, ... or 2, sqrt(2), sqrt(sqrt(2)), sqrt(sqrt(sqrt(2))), .... . They use the graphs of the functions to explain the behavior of the sequences obtained. They extend these explorations by iterating functions they program into the calculator, such as linear functions, where slope is the predictor of behavior, and quadratic functions f (x) = ax (1 - x), where 0< x <1 and 1< a <4, which exhibit chaotic behavior.

• Students explore iteration behavior using the function defined by the two cases

  f(x) = x + 1/2	for x between 0 and 1/2
  f(x) = 2 - 2x	for x between 1/2 and 1

  They use the initial values 1/2, 2/3, 5/9, and 7/10, and then, with a calculator or computer, the initial values .501, .667, and .701 (which differ by a small amount from the first group of "nice" initial values). They compare the behavior of the sequences generated by these values to the sequences generated by the previous initial values.

• Students play the Chaos Game. Each pair of students is provided with an identical transparency on which have been drawn the three vertices L, T, and R of an equilateraltriangle. Each team starts by selecting any point on the triangle. They roll a die and create a new point halfway to L if they roll 1 or 2, halfway to R if they roll 3 or 4, and halfway to T if they roll 5 or 6. They repeat 20 times, each time using the new point as the starting point for the next iteration. The teacher overlays all of the transparencies and out of this chaos comes ... the familiar Sierpinski triangle. (The Sierpinski triangle is discussed in detail in the sections for earlier grade levels. Also see Unit 2 in Fractals for the Classroom. The Chaos Game software allows students to try variations and explore the game further.)

15. Apply discrete methods to storing, processing, and communicating information.

• Students discuss various algorithms used for sorting large numbers of items alphabetically or numerically, and explain why some sorting algorithms are substantially faster than others. To introduce the topic of sorting, give each group of students 100 index cards each with one word on it, and let them devise strategies for efficiently putting the cards into alphabetical order.

• Students discuss how scanners of bar codes (zip codes, UPCs, and ISBNs) are able to detect errors in reading the codes, and evaluate and compare how error-detection is accomplished in different codes. (See the COMAP Module Codes Galore or Chapter 9 of For All Practical Purposes.)

• Students investigate methods of error correction used to transmit digitized pictures from space (Voyager or Mariner probes, or the Hubble space telescope) over noisy or unreliable channels, or to ensure the fidelity of a scratched CD recording. (See Chapter 10 of For All Practical Purposes.)

• Students read about coding and code-breaking machines and their role in World War II.

• Students research topics that are currently discussed in the press, such as public-key encryption, enabling messages to be transmitted securely, and data-compression, used to save space on a computer disk.

16. Apply discrete methods to problems of voting, apportionment, and allocations, and use fundamental strategies of optimization to solve problems.

• Students find the best route when a number of alternate routes are possible. For example: In which order should you pick up the six friends you are driving to the school dance? In which order should you make the eight deliveries for the drug store where you work? In which order should you visit the seven "must-see" sites on your vacation trip? In each case, you want to find the "best route," the one which involves the least total distance, or least total time, or least total expense. Students create their own problems, using actual locations and distances, and find the best route. For a larger project, students can try to improve the route taken by their school bus.

• Students study the role of apportionment in American history, focusing on the 1790 census (acting out the positions of the thirteen original states and discussing George Washington's first use of the presidential veto), and the disputed election of 1876, and discuss the relative merits of different systems of apportionment that have been proposed and used. (This activity provides an opportunity for mathematics and history teachers to work together.) They also devise a student government where the seats are fairly apportionedamong all constituencies. (See the COMAP module The Apportionment Problem or Chapter 14 of For All Practical Purposes.)

• Students analyze mathematical methods for dividing an estate fairly among various heirs. (See Chapter 2 of Discrete Mathematics Through Applications, Chapter 3 of Excursions in Modern Mathematics, or Chapter 13 of For All Practical Purposes.)

• Students discuss various methods, such as preference schedules or approval voting, that can be used for determining the winner of an election involving three or more candidates (for example, the prom king or queen). With preference schedules, each voter ranks the candidates and the individual rankings are combined, using various techniques, to obtain a group ranking; preference schedules are used, for example, in ranking sports teams or determining entertainment awards. In approval voting, each voter can vote once for each candidate which she finds acceptable; the candidate who receives the most votes then wins the election. (See the COMAP module The Mathematical Theory of Elections or Chapter 11 of For All Practical Purposes.)

• Students find an efficient way of doing a complex project (like preparing an airplane for its next trip) given which tasks precede which and how much time each task will take. (See Chapter 8 of Excursions of Modern Mathematics or Chapter 3 of For All Practical Purposes.)

• Students find an efficient way of assigning songs of various lengths to the two sides of an audio tape so that the total times on the two sides are as close together as possible. Similarly, they determine the minimal number of sheets of plywood needed to build a cabinet with pieces of specified dimensions.

• Students apply algorithms for matching in graphs to schedule when contestants play each other in the different rounds of a tournament.

• Students devise a strategy for finding a "secret number" from 1 to 1000 using questions of the form Is your number bigger than 837? and determine the least number of questions needed to find the secret number.

References

Bennett, S., D. DeTemple, M. Dirks, B. Newell, J. Robertson, and B. Tyus. The Apportionment Problem: The Search for the Perfect Democracy. Consortium for Mathematics and Its Applications (COMAP), Module #18, 1986.

Chavey, D. Drawing Pictures with One Line. Consortium for Mathematics and Its Applications (COMAP), Module #21, 1987.

Consortium for Mathematics and Its Applications. For All Practical Purposes: Introduction to Contemporary Mathematics. W. H. Freeman and Company,Third Edition, 1993.

Crisler, N., P. Fisher, and G. Froelich, Discrete Mathematics Through Applications. W. H. Freeman and Company, 1994.

Francis, R. The Mathematician's Coloring Book. Consortium for Mathematics and Its Applications (COMAP), Module #13, 1989.

Garland, T. H. Fascinating Fibonaccis. Palo Alto, CA: Dale Seymour Publications, 1987.

Kenney, M. J., Ed. Discrete Mathematics Across the Curriculum K-12, 1991 Yearbook of the National Council of Teachers of Mathematics (NCTM). Reston, VA, 1991.

Malkevitch, J. The Mathematical Theory of Elections. Consortium for Mathematics and Its Applications (COMAP). Module #1, 1985.

Malkevitch, J., G. Froelich, and D. Froelich. Codes Galore. Consortium for Mathematics and Its Applications (COMAP). Module #18, 1991.

Peitgen, Heinz-Otto, et al. Fractals for the Classroom: Strategic Activities Volume One & Two. Reston, VA: NCTM and New York: Springer-Verlag, 1992.

Rosenstein, J. G., D. Franzblau, and F. Roberts, Eds. Discrete Mathematics in the Schools: Making an Impact. Proceedings of a 1992 DIMACS Conference on "Discrete Mathematics in the Schools." DIMACS Series on Discrete Mathematics and Theoretical Computer Science. Providence, RI: American Mathematical Society (AMS), 1997. (Available online from this chapter in http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/.)

Seymour, D. Patterns in Pascal's Triangle. Poster. Palo Alto, CA: Dale Seymour Publications.

Tannenbaum, P. and R. Arnold. Excursions in Modern Mathematics. Prentice-Hall, 1992.

Software

The Chaos Game. Minnesota Educational Computer Consortium (MECC).

On-Line Resources

http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/

The Framework will be available at this site during Spring 1997. In time, we hope to post additional resources relating to this standard, such as grade-specific activities submitted by New Jersey teachers, and to provide a forum to discuss the Mathematics Standards.