STANDARD 14 - DISCRETE MATHEMATICS
|
All students will apply the concepts and methods of discrete
mathematics to model and explore a variety of practical
situations.
|
Standard 14 - Discrete Mathematics - Grades K-2
Overview
The five major themes of discrete mathematics, as discussed in the
K-12 Overview, are systematic listing, counting, and
reasoning; discrete mathematical modeling using graphs (networks) and
trees; iterative (that is, repetitive) patterns and processes;
organizing and processing information; and following and
devising lists of instructions, called
"algorithms," and using them to find the best
solution to real-world problems.
Despite their formidable titles, these five themes can be addressed
with activities at the K-2 grade level which involve purposeful play
and simple analysis. Indeed, teachers will discover that many
activities they already are using in their classrooms reflect these
themes. These five themes are discussed in the paragraphs below.
 Activities involving systematic listing, counting, and
reasoning can be done very concretely at the K-2 grade level. For
example, dressing cardboard teddy bears with different outfits becomes
a mathematical activity when the task is to make a list of all
possible outfits and count them; pictured on the right are the six
outfits that can be arranged using one of two types of shirts and one
of three types of shorts. Similarly, playing any game involving
choices becomes a mathematical activity when children reflect on the
moves they make in the game.
Activities involving systematic listing, counting, and
reasoning can be done very concretely at the K-2 grade level. For
example, dressing cardboard teddy bears with different outfits becomes
a mathematical activity when the task is to make a list of all
possible outfits and count them; pictured on the right are the six
outfits that can be arranged using one of two types of shirts and one
of three types of shorts. Similarly, playing any game involving
choices becomes a mathematical activity when children reflect on the
moves they make in the game.
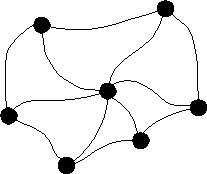 An important discrete mathematical model is that of a
network or graph, which consists of dots and lines
joining the dots; the dots are often called vertices (vertex is
the singular) and the lines are often called edges. (This is
different from other mathematical uses of the term "graph.")
The two terms "network" and "graph" are used
interchangeably for this concept. An example of a graph with seven
vertices and twelve edges is given below. You can think of the
vertices of this graph as islands in a river and the edges as
bridges. You can also think of them as buildings and roads,
or houses and telephone cables, or people and handshakes; wherever a
collection of things are joined by connectors, the mathematical model
used is that of a network or graph. At the K-2 level, children can
recognize graphs and use life-size models of graphs in various ways.
For example, a large version of this graph, or any other graph, can be
"drawn" on the floor using paper plates as vertices and
masking tape as edges. Children might select two "islands"
and find a way to go from one island to the other island by crossing
exactly four "bridges." (This can be done for any two
islands in this graph, but not necessarily in another graph.)
An important discrete mathematical model is that of a
network or graph, which consists of dots and lines
joining the dots; the dots are often called vertices (vertex is
the singular) and the lines are often called edges. (This is
different from other mathematical uses of the term "graph.")
The two terms "network" and "graph" are used
interchangeably for this concept. An example of a graph with seven
vertices and twelve edges is given below. You can think of the
vertices of this graph as islands in a river and the edges as
bridges. You can also think of them as buildings and roads,
or houses and telephone cables, or people and handshakes; wherever a
collection of things are joined by connectors, the mathematical model
used is that of a network or graph. At the K-2 level, children can
recognize graphs and use life-size models of graphs in various ways.
For example, a large version of this graph, or any other graph, can be
"drawn" on the floor using paper plates as vertices and
masking tape as edges. Children might select two "islands"
and find a way to go from one island to the other island by crossing
exactly four "bridges." (This can be done for any two
islands in this graph, but not necessarily in another graph.)
 Children can recognize and work with repetitive patterns
and processes involving numbers and shapes, using objects
in the classroom and in the world around them. For example, children
at the K-2 level can create (and decorate) a pattern of triangles or
squares (as pictured here) that cover a section of the floor (this is
called a "tessellation"), or start with a number and
repeatedly add three, or use clapping and movement to simulate
rhythmic patterns.
Children can recognize and work with repetitive patterns
and processes involving numbers and shapes, using objects
in the classroom and in the world around them. For example, children
at the K-2 level can create (and decorate) a pattern of triangles or
squares (as pictured here) that cover a section of the floor (this is
called a "tessellation"), or start with a number and
repeatedly add three, or use clapping and movement to simulate
rhythmic patterns.
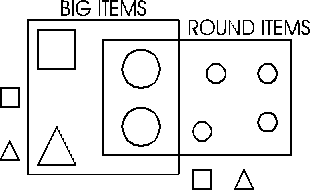 Children at the K-2 grade levels should investigate ways of
sorting items according to attributes like color, shape,
or size, and ways of arranging data into charts, tables, and
family trees. For example, they can sort attribute blocks or stuffed
animals by color or kind, as in the diagram, and can count the number
of children who have birthdays in each month by organizing themselves
into birthday-month groups.
Children at the K-2 grade levels should investigate ways of
sorting items according to attributes like color, shape,
or size, and ways of arranging data into charts, tables, and
family trees. For example, they can sort attribute blocks or stuffed
animals by color or kind, as in the diagram, and can count the number
of children who have birthdays in each month by organizing themselves
into birthday-month groups.
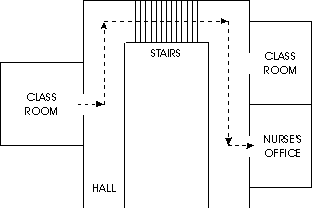
Finally, at the K-2 grade levels, children should be able to
follow and describe simple procedures and determine and discuss
what is the best solution to a problem. For example, they
should be able to follow a prescribed route from the classroom to
another room in the school (as pictured below) and to compare various
alternate routes, and in the second grade should determine the
shortest path from one site to another on a map laid out on the
classroom floor.
Two important resources on discrete mathematics for teachers at all
levels are the 1991 NCTM Yearbook Discrete Mathematics Across the
Curriculum K-12 and the 1997 DIMACS Volume Discrete Mathematics
in the Schools: Making An Impact. Another important
resource for K-2 teachers is This Is MEGA-Mathematics!
Standard 14 - Discrete Mathematics - Grades K-2
Indicators and Activities
The cumulative progress indicators for grade 4 appear below in
boldface type. Each indicator is followed by activities which
illustrate how it can be addressed in the classroom in kindergarten
and grades 1 and 2.
Experiences will be such that all students in grades K-2:
1. Explore a variety of puzzles, games, and
counting problems.
- Students use teddy bear cutouts with, for example, shirts
of two colors and shorts of three colors, and decide how many
different outfits can be made by making a list of all possibilities
and arranging them systematically. (See illustration in K-2
Overview.)
- Students use paper faces or Mr. Potato Head type
models to create a "regular face" given a nose, mouth, and a
pair of eyes. Then they use another pair of eyes, then another nose,
and then another mouth (or other parts) and explore and record the
number of faces that can be made after each additional part has been
included.
- Students read A Three Hat Day and then
try to create as many different hats as possible with three hats, a
feather, a flower, and a ribbon as decoration. Students count the
different hats they've made and discuss their
answers.
- Students count the number of squares of each
size (1 x 1, 2 x 2, 3 x 3) that they can find on the square grid
below. They can be challenged to find the numbers of small squares of
each size on a larger square or rectangular grid.

- Students work in groups to figure out the rules of addition
and placement that are used to pass from one row to the next in the
diagram below, and use these rules to find the numbers in the next few
rows.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
In this diagram, called Pascal's triangle, each number is the
sum of the two numbers that are above it, to its left and right; the
numbers on the left and right edges are all 1.
- Students cut out five "coins" labeled 1 cent,
2 cents, 4 cents, 8 cents, and 16 cents. For each number in the
counting sequence 1, 2, 3, 4, 5, ... (as far as is appropriate for a
particular group ofstudents), students determine how to obtain that
amount of money using a combination of different coins.
- Students play simple games and discuss why they make the
moves they do. For example, two students divide a six-piece domino
set (with 0-0, 0-1, 0-2, 1-1, 1-2, and 2-2) and take turns placing
dominoes so that dominoes which touch have the same numbers and so
that all six dominoes are used in the chain.
2. Use networks and tree diagrams to represent
everyday situations.
- Students find a way of getting from one island
to another, in the graph described in the K-2 Overview laid out on the
classroom floor with masking tape, by crossing exactly four bridges.
They make their own graphs, naming each of the islands, and make a
"from-to" list of islands for which they have found a
four-bridge-route. (Note: it may not always be possible to find
four-bridge-routes.)
- Students count the number of edges at each
vertex (called the degree of the vertex) of a network and
construct graphs where all vertices have the same degree, or where all
the vertices have one of two specified degrees.
-
 On a pattern of islands and bridges laid out on the
floor, students try to find a way of visiting each island exactly
once; they can leave colored markers to keep track of islands already
visited. Note that for some patterns this may not be possible!
Students can be challenged to find a way of visiting each island
exactly once which returns them to their starting point. Similar
activities can be found in Inside, Outside, Loops, and
Lines by Herbert Kohl.
On a pattern of islands and bridges laid out on the
floor, students try to find a way of visiting each island exactly
once; they can leave colored markers to keep track of islands already
visited. Note that for some patterns this may not be possible!
Students can be challenged to find a way of visiting each island
exactly once which returns them to their starting point. Similar
activities can be found in Inside, Outside, Loops, and
Lines by Herbert Kohl.
- Students create a map with make-believe
countries (see example below), and color the maps so that countries
which are next to each other have different colors. How many
colors were used? Could it be done with fewer colors? with
four colors? with three colors? with two colors? A
number of interesting map coloring ideas can be found in Inside,
Outside, Loops and Lines by Herbert Kohl.

3. Identify and investigate sequences and patterns
found in nature, art, and music.
- Students use a calculator to create a sequence of
ten numbers starting with zero, each of which is three more than the
previous one; on some calculators, this can be done bypressing 0 + 3 =
= = . . . , where = is pressed ten times. As they proceed, they count
one 3, two 3s, three 3s, etc.
 Students "tessellate" the plane, by using
groups of squares or triangles (for example, from sets of pattern
blocks) to completely cover a sheet of paper without overlapping; they
record their patterns by tracing around the blocks on a sheet of paper
and coloring the shapes.
Students "tessellate" the plane, by using
groups of squares or triangles (for example, from sets of pattern
blocks) to completely cover a sheet of paper without overlapping; they
record their patterns by tracing around the blocks on a sheet of paper
and coloring the shapes.- Students listen to or read Grandfather
Tang's Story by Ann Tompert and then use tangrams to
make the shape-changing fox fairies as the story progresses. Students
are then encouraged to do a retelling of the story with tangrams or to
invent their own tangram characters and stories.
- Students read The Cat in the Hat or
Green Eggs and Ham by Dr. Seuss and identify the pattern of
events in the book. Students could create their own books with
similar patterns.
- Students collect leaves and note the patterns of the veins.
They look at how the veins branch off on each side of the center vein
and observe that their branches are smaller copies of the original
vein pattern. Students collect feathers, ferns, Queen Anne's
lace, broccoli, or cauliflower and note in each case how the pattern
of the original is repeated in miniature in each of its branches or
clusters.
- Students listen for rhythmic patterns in musical selections
and use clapping, instruments, and movement to simulate those
patterns.
- Students take a "patterns walk"
through the school, searching for patterns in the bricks, the play
equipment, the shapes in the classrooms, the number sequences of
classrooms, the floors and ceilings, etc.; the purpose of this
activity is to create an awareness of all the patterns around
them.
4. Investigate ways to represent and classify data
according to attributes, such as shape or color, and
relationships, and discuss the purpose and usefulness of such
classification.
- Students sort themselves by month of birth, and then within
each group by height or birth date. (Other sorting activities can be
found in Mathematics Their Way, by Mary Baratta-Lorton.)
- Each student is given a card with a different number on it.
Students line up in a row and put the numbers in numerical order by
exchanging cards, one at a time, with adjacent children. (After
practice, this can be accomplished without talking.)
- Students draw stick figures of members of their
family and arrange them in order of size.
- Students sort stuffed animals in various ways and explain
why they sorted them as they did. Students can use Tabletop,
Jr. software to sort characters according to a variety of
attributes.
- Using attribute blocks, buttons, or other objects with
clearly distinguishable attributes such as color, size, and shape,
students develop a sequence of objects where each differs from the
previous one in only one attribute. Tabletop, Jr. software can
also be used to create such sequences of objects.
- Students use two Hula Hoops (or large circles drawn on
paper so that a part of their interiors overlap) to assist in sorting
attribute blocks or other objects according to two characteristics.
For example, given a collection of objects of different colors and
shapes, students are asked to place them so that all red items go
inside hoop #1 and all others go on the outside, and so that all
square items go inside hoop #2 and all others go on the outside.
What items should be placed in the overlap of the two hoops? What
is inside only the first hoop? What is outside both
hoops?
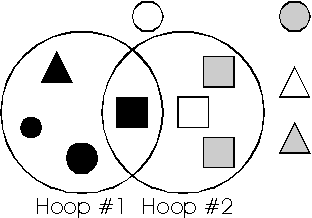
This is an example of a Venn diagram. Students can also use Venn
diagrams to organize the similarities and differences between the
information in two stories by placing all features of the first story
in hoop #1 and all features of the second story in hoop #2, with
common features in the overlap of the two hoops. A similar activity
can be found in the Shapetown lesson that is described in the
First Four Standards of this Framework. Tabletop, Jr.
software allows students to arrange and sort data, and to explore
these concepts easily.
5. Follow, devise, and describe practical lists of
instructions.
- Students follow directions for a trip within the classroom
- for example, students are asked where they would end up if they
started at a given spot facing in a certain direction, took three
steps forward, turned left, took two steps forward, turned right, and
moved forward three more steps.
- Students follow oral directions for going from the
classroom to the lunchroom, and represent these directions with a
diagram. (See K-2 Overview for a sample diagram.)
- Students agree on a procedure for filling a box with
rectangular blocks. For example, a box with dimensions
4"x4"x5" can be filled with 10 blocks of dimensions
1"x2"x4". (Linking cubes can be used to create the
rectangular blocks.)
- Students explore the question of finding the shortest route
from school to home on a diagram like the one pictured below, laid out
on the floor using masking tape, where students place a number of
counters on each line segment to represent the length of that segment.
(The shortest route will depend on the placement of the counters; what
appears to be the most direct route may not be the shortest.)
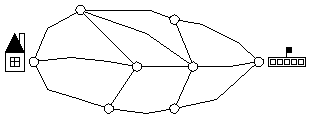
- Students find a way through a simple maze. They
discuss the different paths they took and their reasons for doing
so.
- Students use Logo software to give the turtle
precise instructions for movement in specified
directions.
References
-
Baratta-Lorton, Mary. Mathematics Their Way. Menlo Park,
CA: Addison Wesley, 1993.
Casey, Nancy, and Mike Fellows. This is MEGA-Mathematics!
- Stories and Activities for
Mathematical Thinking, Problem-Solving, and Communication.
Los Alamos, CA: Los Alamos National Laboratories, 1993. (A
version is available online at
http://www.c3.lanl.gov/mega-math)
Geringer, Laura. A Three Hat Day. New York: Harper Row
Junior Books, 1987.
Kenney, M. J., Ed. Discrete Mathematics Across the Curriculum
K-12. 1991 Yearbook of the National Council of Teachers of
Mathematics (NCTM). Reston, VA: 1991.
Kohl, Herbert. Insides, Outsides, Loops, and Lines. New
York: W. H. Freeman, 1995.
Murphy, Pat. By Nature's Design. San
Francisco, CA: Chronicle Books, 1993.
Rosenstein, J. G., D. Franzblau, and F. Roberts, Eds.
Discrete Mathematics in the Schools:
Making an Impact. Proceedings of a 1992 DIMACS Conference
on "Discrete Mathematics in the Schools." DIMACS Series
on Discrete Mathematics and Theoretical Computer Science.
Providence, RI: American Mathematical Society (AMS), 1997.
(Available online from this chapter in
http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/.)
Seuss, Dr. Cat in the Hat. Boston, MA: Houghton
Mifflin, 1957.
Seuss, Dr. Green Eggs and Ham. Random House.
Tompert, Ann. Grandfather Tang's Story.
Crown Publishing, 1990.
Software
-
Logo. Many versions of Logo are commercially
available.
Tabletop, Jr. Broderbund Software. TERC.
On-Line Resources
-
http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/
The Framework will be available at this site during
Spring 1997. In time, we hope to post additional resources
relating to this standard, such as grade-specific activities submitted
by New Jersey teachers, and to provide a forum to discuss the
Mathematics Standards.
|

 Activities involving systematic listing, counting, and
reasoning can be done very concretely at the K-2 grade level. For
example, dressing cardboard teddy bears with different outfits becomes
a mathematical activity when the task is to make a list of all
possible outfits and count them; pictured on the right are the six
outfits that can be arranged using one of two types of shirts and one
of three types of shorts. Similarly, playing any game involving
choices becomes a mathematical activity when children reflect on the
moves they make in the game.
Activities involving systematic listing, counting, and
reasoning can be done very concretely at the K-2 grade level. For
example, dressing cardboard teddy bears with different outfits becomes
a mathematical activity when the task is to make a list of all
possible outfits and count them; pictured on the right are the six
outfits that can be arranged using one of two types of shirts and one
of three types of shorts. Similarly, playing any game involving
choices becomes a mathematical activity when children reflect on the
moves they make in the game. An important discrete mathematical model is that of a
network or graph, which consists of dots and lines
joining the dots; the dots are often called vertices (vertex is
the singular) and the lines are often called edges. (This is
different from other mathematical uses of the term "graph.")
The two terms "network" and "graph" are used
interchangeably for this concept. An example of a graph with seven
vertices and twelve edges is given below. You can think of the
vertices of this graph as islands in a river and the edges as
bridges. You can also think of them as buildings and roads,
or houses and telephone cables, or people and handshakes; wherever a
collection of things are joined by connectors, the mathematical model
used is that of a network or graph. At the K-2 level, children can
recognize graphs and use life-size models of graphs in various ways.
For example, a large version of this graph, or any other graph, can be
"drawn" on the floor using paper plates as vertices and
masking tape as edges. Children might select two "islands"
and find a way to go from one island to the other island by crossing
exactly four "bridges." (This can be done for any two
islands in this graph, but not necessarily in another graph.)
An important discrete mathematical model is that of a
network or graph, which consists of dots and lines
joining the dots; the dots are often called vertices (vertex is
the singular) and the lines are often called edges. (This is
different from other mathematical uses of the term "graph.")
The two terms "network" and "graph" are used
interchangeably for this concept. An example of a graph with seven
vertices and twelve edges is given below. You can think of the
vertices of this graph as islands in a river and the edges as
bridges. You can also think of them as buildings and roads,
or houses and telephone cables, or people and handshakes; wherever a
collection of things are joined by connectors, the mathematical model
used is that of a network or graph. At the K-2 level, children can
recognize graphs and use life-size models of graphs in various ways.
For example, a large version of this graph, or any other graph, can be
"drawn" on the floor using paper plates as vertices and
masking tape as edges. Children might select two "islands"
and find a way to go from one island to the other island by crossing
exactly four "bridges." (This can be done for any two
islands in this graph, but not necessarily in another graph.) Children can recognize and work with repetitive patterns
and processes involving numbers and shapes, using objects
in the classroom and in the world around them. For example, children
at the K-2 level can create (and decorate) a pattern of triangles or
squares (as pictured here) that cover a section of the floor (this is
called a "tessellation"), or start with a number and
repeatedly add three, or use clapping and movement to simulate
rhythmic patterns.
Children can recognize and work with repetitive patterns
and processes involving numbers and shapes, using objects
in the classroom and in the world around them. For example, children
at the K-2 level can create (and decorate) a pattern of triangles or
squares (as pictured here) that cover a section of the floor (this is
called a "tessellation"), or start with a number and
repeatedly add three, or use clapping and movement to simulate
rhythmic patterns. Children at the K-2 grade levels should investigate ways of
sorting items according to attributes like color, shape,
or size, and ways of arranging data into charts, tables, and
family trees. For example, they can sort attribute blocks or stuffed
animals by color or kind, as in the diagram, and can count the number
of children who have birthdays in each month by organizing themselves
into birthday-month groups.
Children at the K-2 grade levels should investigate ways of
sorting items according to attributes like color, shape,
or size, and ways of arranging data into charts, tables, and
family trees. For example, they can sort attribute blocks or stuffed
animals by color or kind, as in the diagram, and can count the number
of children who have birthdays in each month by organizing themselves
into birthday-month groups.
 On a pattern of islands and bridges laid out on the
floor, students try to find a way of visiting each island exactly
once; they can leave colored markers to keep track of islands already
visited. Note that for some patterns this may not be possible!
Students can be challenged to find a way of visiting each island
exactly once which returns them to their starting point. Similar
activities can be found in Inside, Outside, Loops, and
Lines by Herbert Kohl.
On a pattern of islands and bridges laid out on the
floor, students try to find a way of visiting each island exactly
once; they can leave colored markers to keep track of islands already
visited. Note that for some patterns this may not be possible!
Students can be challenged to find a way of visiting each island
exactly once which returns them to their starting point. Similar
activities can be found in Inside, Outside, Loops, and
Lines by Herbert Kohl.
 Students "tessellate" the plane, by using
groups of squares or triangles (for example, from sets of pattern
blocks) to completely cover a sheet of paper without overlapping; they
record their patterns by tracing around the blocks on a sheet of paper
and coloring the shapes.
Students "tessellate" the plane, by using
groups of squares or triangles (for example, from sets of pattern
blocks) to completely cover a sheet of paper without overlapping; they
record their patterns by tracing around the blocks on a sheet of paper
and coloring the shapes.
