Finding the
"Middle" of a Graph
and Why it Matters
Joseph Malkevitch
Mathematics and Computing Dept.
York College (CUNY)
Jamaica, New York 11451
What is the public's
perception of
mathematics and
mathematicians?
Typical response:
Mathematics is a sea of problems involving symbols whose meaning I can not understand!
Samples:
(x2)- 5 = ?
x/(x-3) + (x-4)/(x+7) = ?
X2(y - 4x) - y(3X2 + 3Y) = ?
3x - 2(5x - 4) = 8 (Solve for x)
Typical response:
Mathematicians are aging males who wear beards and glasses and if they have any hair, it's a mess
or
Albert Einstein is the
greatest living
mathematician.
Neither the general public nor surprisingly large parts of the scientific community are aware of:
a. The dramatic growth in new mathematical tools.
b. The role of mathematics in the development of many recent technologies.
Examples:
Medical imaging
Fax and wireless communication
Compact disc and CD-ROM technology
Fuel efficient transportation
Mapping the human genome
c. The emerging role of mathematics in areas outside of the sciences and engineering.
Examples:
Political science
Applications: elections, legislative apportionment, weighted voting, political gamesEconomics
Applications: bankruptcy, fair allocation, cost sharing, equilibrium prices, efficiency, gamesBusiness
Applications: bargaining, optimization, security, fairness, new financial instrumentsAccounting
Applications: internal cost sharing, financial instruments, generational equityFine arts
Applications: fabric design, classification of patterns
Mathematics can be
viewed as a subject which
has concerns with various
themes
in contrast with various
techniques.
Techniques:
0. Arithmetic
1. Algebra
2. Geometry
3. Trigonometry
4. Calculus
5. Linear (Matrix) Algebra
6. Probability and Statistics
7. Graph Theory
8. Modern Algebra
9. Coding Theory
10. Knot Theory
(Many more!)
Themes
1. Optimization
2. Growth and Change
3. Information
4. Fairness and Equity
5. Risk
6. Shape and Space
7. Pattern and Symmetry
8. Order and Disorder
9. Reconstruction
10. Conflict and Cooperation
11. Unintuitive behavior
Example:
What is the best
location for a
hospital in this community?
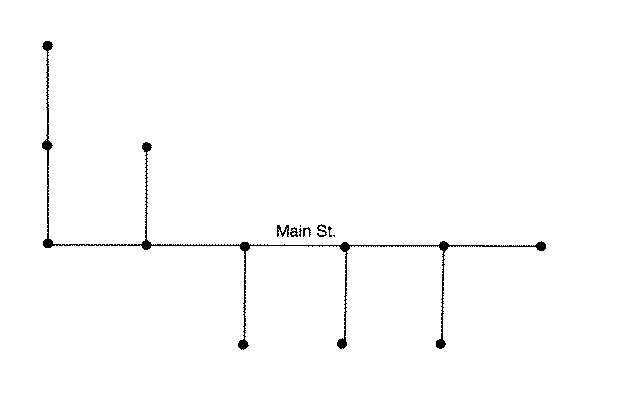
How would your analysis differ
if the problem involved locating a
firehouse a school, or a super-market?
What difference is there if a facility must
be at a vertex versus located somewhere
along an edge?
Distance:
* Two points in space
* Insulin molecules in a gorilla and chimpanzee
* Two relatives
* Preference schedules of two voters
* Two images or texts
* Two code words
Distances between two points in space:
Euclidean distance
Taxicab distance
Max distance
Abstract properties of distance:
1. Distance is a non-negative real number.
2. The distance between two points is zero if and only if they are the same.
3. The distance between p and q is the same as the distance between q and p.
4. The triangle inequality: The distance from p to q plus the distance from q to r is at least as large as the distance from p to r.
Eccentricity of a vertex v:
Maximum distance any vertex can be from v
Central vertex:
Vertex with minimum value for its eccentricity
Center:
Subgraph induced by the central vertices of a graph
Jordan's Theorem:
The center of a tree is either a single vertex or a pair of vertices joined by an edge.
Exercise:
A tree has one central vertex if and only
if the diameter of the tree is twice its radius.
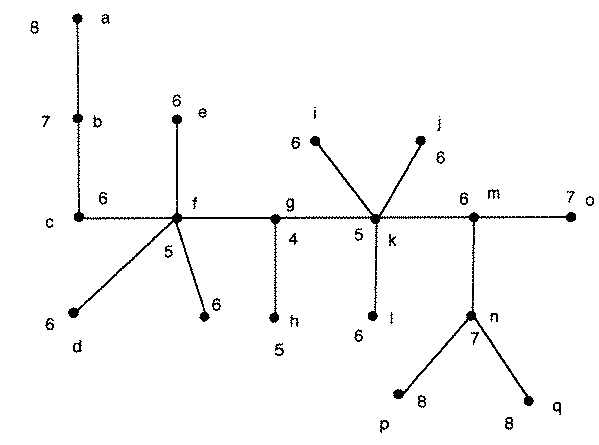
Numbers are eccentricities of the vertices.
Branch weight:

Numbers show the branch weights of the vertices.