A matching in G is a set M of edges of G, no two of which share a vertex. The matching M is a maximum matching in G if G has no matching with more edges then M. The size of any maximum matching of G is called the matching number of g denoted by alpha' (G).
The matching M is said to be saturate vertex v if v is an end of an edge of M, otherwise v is said to be M-unsaturated. The vertex v is universal in G if every maximum matching of G saturates v, so lambda' (G/v)=alpha' (G)-1. (And conversely, if v is not universal in G, then alpha' (G/v)=alpha' (G).
The Slither Theorem
I.) If v0 is universal in G, then the first player can force a win in Slither as follows. Let M be any maximum matching in G. The first players winning strategy is to always pick edges from M.
II.)If v0 is not universal in G, then the second player can force a win in Slither as follows. Let
M be any maximum matching in G not saturating v0. The second playerís winning strategy is to always pick edges from M.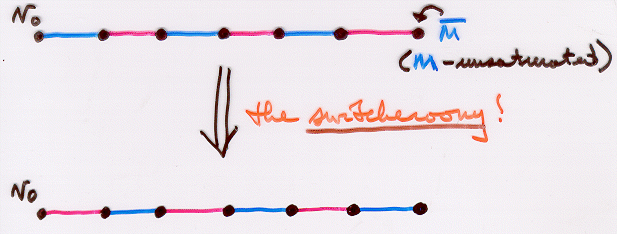
M'
is a maximum matching not saturating v0.IV.)What if player 2 canít follow the strategy?

M'
is a layer matching.An M-alternating path is a path whose edges are alternately in M and not in M. An M-augmenting path is an M-alternating path with two M-unsaturated ends.
True Fact
If there is an M-augmenting path,
then M is not a maximum matching.
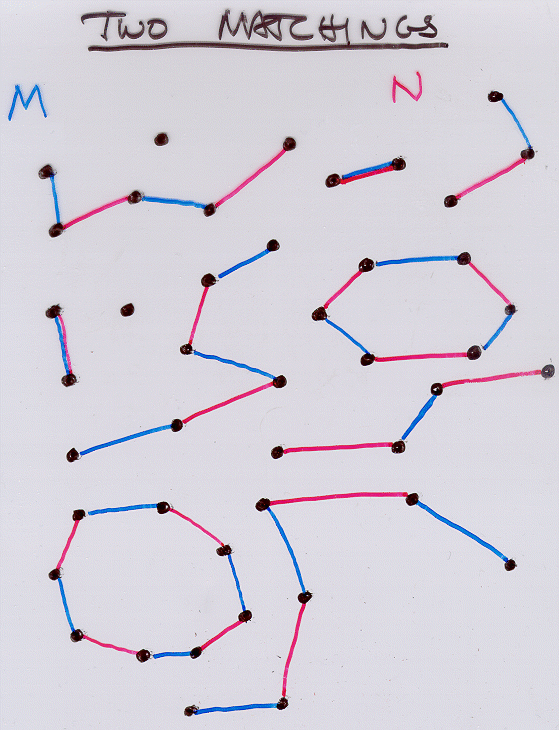
Let
M and N be matching in G, let H be the graph with the same vertex set as G, and edges M (union) N. Then the components of H are each, one of the following six types.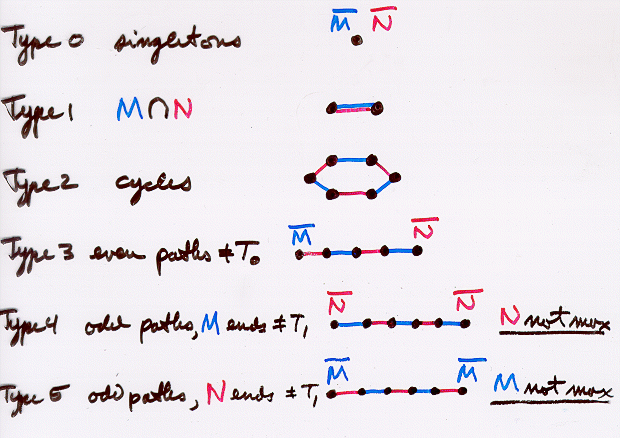
Claude Berge's Theorem
Let M be a matching in G that is not maximum. Then G has an M-augmenting path.
Proof: Let
N be a larger matching. Then H must have a type 5 component, which in an M-augmenting path.Dom de Cain's Theorem
Let e=uv be an edge of G. Then:
Either
1.u is universal in G
2.v is universal in G
3.e is part of an odd cycle
Proof: If #1 is not true let
M be a maximum matching not saturating u. Then M must saturate v, otherwise M u{e} would be a larger matching. Similarly, if #2 is not true then there is a maximum matching N not saturating v, which must saturate u:
For each vertex x, let Tx be the component of H containing x. Then Tu and Tv are paths of type 3. If Tu does not equal Tv , preform a switcheroony on Tv:
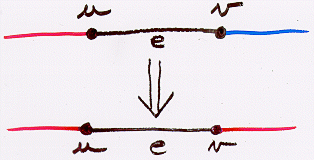
This produces a larger matching
M' u{e}, a contradiction. Thus Tu = Tv, and Tu u{e} is an odd cycle, so #3 Holds.Theorem
Let G be a connected graph on n vertices, non of which are universal. Then u is odd, and alpha'(G)=1/2(n-1)