THE FIRST FOUR STANDARDSSTANDARD 4 - REASONINGK-12 Overview
Descriptive StatementMathematical reasoning is the critical skill that enables a student to make use of all other mathematical skills. With the development of mathematical reasoning, students recognize that mathematics makes sense and can be understood. They learn how to evaluate situations, select problem-solving strategies, draw logical conclusions, develop and describe solutions, and recognize how those solutions can be applied. Mathematical reasoners are able to reflect on solutions to problems and determine whether or not they make sense. They appreciate the pervasive use and power of reasoning as a part of mathematics. Meaning and ImportanceThere are various terms used to refer to "reasoning": critical thinking, higher-order thinking, logical reasoning, or simply reasoning. Different subject areas tend to use different terms. Across all of these subject areas, however, there are commonalities. The following phrases often appear in discussions of how reasoning is used (adapted from Resnick, 1987, pp 2-3):
K-12 Development and EmphasesEvery student has potential for higher-order thinking. The key is to unlock the world of mathematics through a student's natural inclination to strive for purpose and meaning. Reasoning is fundamental to the knowing and doing of mathematics. Conjecturing and demonstrating the logical validity of conjectures are the essence of the creative act of doing mathematics. To give more students access to mathematics as a powerful way of making sense of the world, it is essential that an emphasis on reasoning pervade all mathematical activity. In order to become confident, self-reliant mathematical thinkers, students need to develop the capability to confront a mathematical problem, persevere in its solution, and evaluate and justify their results. Inductive reasoning involves looking for patterns and making generalizations. For example, students use this type of reasoning when they look at many different parallelograms, and try to list the characteristics they have in common. The reasoning process is enhanced by also considering figures that are not parallelograms and discussing how they are different. 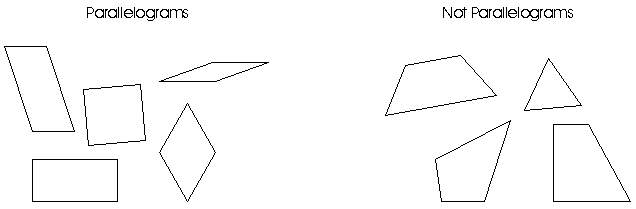
Students may use inductive reasoning to discover patterns in multiplying by ten or a hundred or in working with exponents. Learning mathematics should involve a constant search for patterns, with students making educated guesses, testing them, and then making generalizations. Many students use inductive reasoning more frequently than teachers realize, but the generalizations that they form are not always correct. For example, a student may see the examples 16/64 = 1/4 and 19/95 = 1/5 and reason inductively that the common digits in a fraction may be canceled. The student must realize that she needs to continue to test her conjecture before making such a generalization, since 17/76 is not equal to 1/6, for example. Students must also realize that while inductive reasoning demonstrates the power of mathematics and allows great leaps forward in understanding, it is insufficient in itself. The generalizations that are obtained by using inductive reasoning can only be accepted by "proving" them through deductive reasoning. Deductive reasoning involves making a logical argument, drawing conclusions, and applying generalizations to specific situations. For example, once students have developed an understanding of "parallelogram," they apply that generalization to new figures to decide whether or not each is a parallelogram. This kind of reasoning also may involve eliminating unreasonable possibilities and justifying answers. Although students as young as first graders can recognize valid conclusions, the ability to use deductive reasoning improves as students grow older. More complex reasoning skills, such as recognizing invalid arguments, are appropriate at the secondary level. Understanding the power of reasoning to make sense of mathematics is critical to helping students become self-reliant, independent mathematical thinkers. Students must be able to judge for themselves theaccuracy of their answers; they must be able to apply mathematical reasoning skills in other subject areas and in their daily lives. They must recognize that mathematical reasoning can be used in many different situations to help them make choices and reach decisions. In summary, mathematical reasoning is the glue that binds together all other mathematical skills. By using inductive and deductive reasoning as they learn mathematical concepts and solve mathematical problems, students come to recognize the extent to which reasoning applies to mathematics and to their world. References
|