STANDARD 8 - NUMERICAL OPERATIONS
|
All students will understand, select, and apply various methods of
performing numerical operations.
|
Standard 8 - Numerical Operations - Grades 3-4
Overview
The widespread availability of computing and calculating technology
has given us the opportunity to reconceive the role of computation and
numerical operations in our third and fourth grade mathematics
programs. Traditionally, tremendous amounts of time were spent at
these levels helping children to develop proficiency and accuracy with
paper-and-pencil procedures. Now, adults needing to perform
calculations quickly and accurately have electronic tools that are
both more accurate and more efficient than those procedures. At the
same time, though, the new technology has presented us with a
situation where some numerical operations, skills, and concepts are
much more important than they used to be. As described in the K-12
Overview, estimation, mental computation, and understanding
the meanings of the standard arithmetic operations all play
a more significant role than ever in the everyday life of a
mathematically literate adult.
The major shift in the curriculum that will take place in this
realm, therefore, is one away from drill and practice of
paper-and-pencil procedures with symbols and toward real-world
applications of operations, wise choices of appropriate
computational strategies, and integration of the numerical
operations with other components of the mathematics curriculum.
Third and fourth graders are primarily concerned with cementing
their understanding of addition and subtraction and developing new
meanings for multiplication and division. They should be in an
environment where they can do so by modeling and otherwise
representing a variety of real-world situations in which these
operations are appropriately used. It is important that the variety
of situations to which they are exposed include all the different
scenarios in which multiplication and division are used. There are
several slightly different taxonomies of these types of problems, but
minimally students at this level should be exposed to repeated
addition and subtraction, array, area, and expansion
problems. Students need to recognize and model each of these problem
types for both multiplication and division.
Basic facts in multiplication and division continue to be
very important. Students should be able to quickly and easily recall
quotients and products of one-digit numbers. The most effective
approach to enabling them to acquire this ability has been shown to be
the focused and explicit use of basic fact strategies-conceptual
techniques that make use of the child's understanding of the
operations and number relationships to help recover the appropriate
product or quotient. Doubles and near doubles are
useful strategies, as are discussions and understandings regarding the
regularity in the nines multiplication facts, the roles
of one and zero in these operations, and the roles of
commutativity and distributivity.
Students must still be able to perform two-digit multiplication
and division with paper and pencil, but the widespread
availability of calculators has made the particular procedure used to
perform the calculations less important. It need no longer be the
single fastest, most efficient algorithm chosen without respect to the
degree to which children understand it. Rather, the teaching of
two-digit computation should take on more of a problem solving
approach, a more conceptual, developmental approach. Students should
first use the models of multi-digit numbers that they are most
comfortable with (base ten blocks, money) to explore this new class of
problems. Students who have never formally done two-digit
multiplication might be asked to use their materials to help figure
out how many pencils are packed in the case just received in the
school office. There are 24 boxes with a dozen pencils in each box.
Are there enough for everystudent in the school to have
one? Other, similar, real-world problems would follow, some
involving regrouping and others not.
After initial exploration, students share with each other all of
the strategies they've developed, the best ways they've
found for working with the tens and ones in the problem, and their own
approaches to dealing with the place value issues involved. Most
students can, with direction, take the results of those discussions
and create their own paper-and-pencil procedures for multiplication
and division. The discussions can, of course, include the traditional
approaches, but these ought not to be seen as the only right
way to perform these operations.
Estimation and mental math become critically
important in these grade levels as students are inclined to use
calculators for more and more of their work. In order to use that
technology effectively, third and fourth graders must be able to use
estimation to know the range in which the answer to a given problem
should lie before doing any calculation. They also must be able to
assess the reasonableness of the results of a computation and be
satisfied with the results of an estimation when an exact answer is
unnecessary. Mental mathematics skills, too, play a more important
role in third and fourth grade. Simple two-digit addition and
subtraction problems and those involving powers of ten should be
performed mentally. Students should have enough confidence in their
ability with these types of computations to do them mentally instead
of relying on either a calculator or paper and pencil.
Technology should be an important part of the environment in
third and fourth grade classrooms. Calculators provide a valuable
teaching tool when used to do student-programmed repeated addition or
subtraction, to offer estimation and mental math practice with
target games, and to explore operations and number types that
the students have not yet formally encountered. Students should also
use calculators routinely to find answers to problems that they might
not be able to find otherwise. This use prevents the need to
artificially contrive real-world problems so that their answers are
numbers with which the students are already comfortable.
The topics that should comprise the numerical operations focus of
the third and fourth grade mathematics program are:
- multiplication and division basic facts
- multi-digit whole number addition and subtraction
- two-digit whole number multiplication and division
- decimal addition and subtraction
- explorations with fraction operations
Standard 8 - Numerical Operation - Grades 3-4
Indicators and Activities
The cumulative progress indicators for grade 4 appear below in
boldface type. Each indicator is followed by activities which
illustrate how it can be addressed in the classroom in grades 3 and
4.
Building upon knowledge and skills gained in the preceding grades,
experiences in grades 3-4 will be such that all students:
1. Develop meaning for the four basic arithmetic
operations by modeling and discussing a variety of
problems.
- Students broaden their initial understanding of
multiplication as repeated addition by dealing with situations
involving arrays, expansions, and combinations. Questions of these
types are not easily explained through repeated addition: How many
stamps are on this 7 by 8 sheet? How big would this painting
be if it was 3 times as big? How many outfits can you make
with 2 pairs of pants and 3 shirts?
- Students use counters to model both repeated subtraction
(There are 12 cookies. How many bags of 3?) and
sharing (There are 12 cookies and 3 friends. How many
cookies each?) meanings for division and write about the
difference in their journals.
- Students work through the Sharing Cookies
lesson that is described in the First Four Standards of this
Framework. They investigate division by using 8 cookies to be
shared equally among 5 people, and discuss the problem of simplifying
the number sentence which describes the amount of each person's
share.
- From the beginning of their work with division, children
are asked to make sense out of remainders in problem situations. The
answers to these three problems are different even though the division
is the same: How many cars will we need to transport 19 people if
each car holds 5? How many more packages of 5 ping-pong balls
can be made if there are 19 balls left in the bin? How much
does each of 5 children have to contribute to the cost of a $19
gift?
- Students explore division by reading The
Doorbell Rang by Pat Hutchins. In this story, Victoria and Sam
must share 12 cookies with increasing numbers of friends. Students
can use counters to show how many cookies each person
gets.
- Students learn about multiplication as an array
by reading One Hundred Hungry Ants by Elinor Pinczes, Lucy
and Tom's 1, 2, 3 by Shirley Hughes or Number
Families by Jane Srivastava.
- Students make books showing things that come in
3's, 4's, 5's, 6's, or 12's.
2. Develop proficiency with and memorize
basic number facts using a variety of fact strategies
(such as "counting on" and
"doubles").
- Students use streets and alleys as both a mental
model of multiplication and a useful way to recover facts when needed.
It simply involves drawing a series of horizontal lines(streets) to
represent one factor and a series of vertical lines (alleys) crossing
them to represent the other. The number of intersections of the
streets and alleys is the product!
- Students use a double maker on a calculator for
practice with doubles. They enter x 2 = on the calculator.
Any number pressed then, followed by the equal sign, will show the
number's double. Students work together to try to say the double
for each number before the calculator shows it.
- Students regularly use doubles, near doubles, and
use a related fact strategies for multiplication; they are
using the near doubles strategy when they calculate a sum like
15 + 17 by recognizing that it is 2 more than double
15. More generally, they are using the use a related
fact strategy when they use any fact they happen to remember, like
8 + 4 = 12, to make a related calculation like 8 + 5
=12 + 1 = 13. They also recover facts by knowledge of the role of
zero and one in multiplication, of commutativity, and of the regular
patterned behavior of multiples of nines. Practice sets of problems
are structured so that use of all these strategies is encouraged and
the students are regularly asked to explain the procedures they are
using.
- Pairs of students play Circles and Stars
(Burns, 1991). Each student rolls a die and draws as many circles as
the number shown, then rolls again and puts that number of stars in
every circle, and then writes a multiplication number sentence and
records how many stars there are all together. Each student takes
seven turns, and adds the total. The winner is the student with the
most stars.
- Students use color tiles to show how a given
number of candies can be arranged in a rectangular box.
- Students play multiplication war, using a
deck of cards with kings and queens removed. All of the cards are
dealt out. Each player turns up two cards and multiplies their values
(Jacks count as 0; aces count as 1). The
"general" draws a target number from a hat. The player
closest to the target wins a point. The first player to get 10
points wins the game.
- Students use computer programs such as Math
Workshop to practice multiplication facts.
3. Construct, use, and explain procedures for
performing whole number calculations in the various methods of
computation.
- Students work through the Product and Process
lesson that is described in the Introduction to this Framework.
It challenges students to use calculators and four of the five digits
1, 3, 5, 7, and 9 to discover the multiplication
problem that gives the largest product.
-
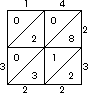 Students explore lattice multiplication and try to figure out
how it works. For example, the figure at the right shows 14
× 23 = 322.
Students explore lattice multiplication and try to figure out
how it works. For example, the figure at the right shows 14
× 23 = 322.
- Students use the skills they've developed with arrow
puzzles (See Standard 6-Number Sense-Grades
3-4-Indicator 3) to practice mental addition and subtraction of
2- and 3-digit numbers. To add 23 to 65, for instance,
they start at 65 on their "mental hundred number
chart," go down twice and to the right three times.
- Students use base ten blocks to help them decide
how many blocks there would be in eachgroup if they divided 123 blocks
among 3 people. The students describe how they used the blocks to
help them solve the problem and compare their solutions and solution
strategies.
4. Use models to explore operations with fractions and
decimals.
- Students use fraction circle pieces (each unit
fraction a different color) to begin to explore addition of fractions.
Questions like: Which of these sums are greater than 1? and
How do you know? are frequent.
- Students use the base ten models that they are most
familiar with for whole numbers and relabel the components with
decimal values. Base ten blocks represent 1 whole, 1 tenth, 1
hundredth, and 1 thousandth. Coins, which had represented a whole
number of cents, now represent hundredths of dollars.
- Students operate a school store with school supplies
available for sale. Other students, using play money, decide on
purchases, pay for them, receive and check on the amount of
change.
- In groups, students each roll a number cube and
use dimes to represent the decimal rolled. For example, a student
rolling a 4 would take 4 dimes to represent 4 tenths of a
dollar. When a student gets 10 dimes, he turns them in for a dollar.
The first student to get $5 wins the game.
- Students use money to represent fractions. For
example, a quarter and a quarter equals half a dollar.
- Students demonstrate equivalent fractions using
pattern blocks. For example, if a yellow hexagon is one whole, then
three green triangles (3/6) is the same size as one red
trapezoid (1/2). Pattern blocks may also be used to represent
addition and subtraction of fractions.
5. Use a variety of mental computation and estimation
techniques.
- Students frequently do warm-up drills that enhance their
mental math skills. Problems like: 3,000 x 7 = , 200
x 6 = , and 5,000 x 5 + 5 = are put on the
board as individual children write the answers without doing any
paper-and-pencil computation.
- Students make appropriate choices from among
front-end, rounding, and compatible numbers
strategies in their estimation work depending on the real-world
situation and the numbers involved. Front end strategies
involve using the first digits of the largest numbers to get an
estimate, which of course is too low, and then adjusting
up. Compatible numbers involves finding some numbers which can
be combined mentally, so that, for example, 762 + 2,444 + 248
is about (750 + 250) + 2,500, or 3,500.
- Students use money and shopping situations to practice
estimation and mental math skills. Is $20.00 enough to buy items
priced at $12.97, $4.95, and 3.95? About how much would 4 cans
of beans cost if each costs $0.79?
- Students explore estimation involving division as
they read The Greatest Guessing Game: A Book about Dividing
by Robert Froman. A little girl and her three friends solve a
variety of problems, estimating first and discussing what to do with
remainders.
6. Select and use appropriate computational methods from
mental math, estimation, paper-and-pencil, and calculator
methods, and check the reasonableness of results.
- Students play addition max out. Each
student has a 2 x 3 array of blanks (in standard 3-digit addition
form) into each of which will be written a digit. One student rolls a
die and everyone must write the number showing into one of their
blanks. Once the number is written in, it can not be changed.
Another roll - another number written, and so on. The object is
to be the player with the largest sum when all six digits have been
written. If a player has the largest possible sum that can be made
from the six digits rolled, there is a bonus for maxing
out.
- Students discuss this problem from the NCTM Standards
(p. 45): Three fourth grade teachers decided to take their
classes on a picnic. Mr. Clark spent $26.94 for refreshments.
He used his calculator to see how much the other two teachers should
pay him so that all three could share the cost equally. He
figured they each owed him $13.47. Is his answer reasonable?
As a follow-up individual assessment, they write about how they
might find an answer.
7. Understand and use relationships among
operations and properties of operations.
- Students take 7x8 block rectangular grids printed
on pieces of paper. They each cut along any one of the 7
block-long segments to produce two new rectangles, for example, a
7x6 and a 7x2 rectangle. They then discuss all of the
different rectangle pairs they produced and how they are all related
to the original one.
- Students write a letter to a second grader explaining why
2+5 equals 5+2 to demonstrate their understanding of
commutativity.
- Students explore modular, or clock, addition as an
operation that behaves differently from the addition they know how to
do. For example: 6 hours after 10 o'clock in the
morning is 4 o'clock in the afternoon, so 10 + 6 =
4 on a 12-hour clock. How is clock addition different
from regular addition? How is it the same? How would modular
subtraction and multiplication work?
References
-
Burns, Marilyn. Math By All Means: Multiplication, Grade 3.
New Rochelle, New York: Cuisenaire, 1991.
Froman, Robert. The Greatest Guessing Game: A Book About
Dividing. New York: Thomas Y. Crowell Publishers, 1978.
Hughes, Shirley. Lucy and Tom's 1, 2, 3. New
York: Viking Kestrel, 1987.
Hutchins, Pat. The Doorbell Rang. New York: Greenwillow
Books, 1986.
National Council of Teachers of Mathematics. Curriculum and
Evaluation Standards for School
Mathematics. Reston, VA, 1989.
Pinczes, Elinor J. One Hundred Hungry Ants. Boston:
Houghton Mifflin Company, 1993.
Srivastava, Jane. Number Families. New York: Thomas
Y. Crowell, 1979.
Software
-
Math Workshop. Broderbund.
On-Line Resources
-
http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/
The Framework will be available at this site during
Spring 1997. In time, we hope to post additional resources
relating to this standard, such as grade-specific activities submitted
by New Jersey teachers, and to provide a forum to discuss the
Mathematics Standards.
|
 Students explore lattice multiplication and try to figure out
how it works. For example, the figure at the right shows 14
× 23 = 322.
Students explore lattice multiplication and try to figure out
how it works. For example, the figure at the right shows 14
× 23 = 322.