STANDARD 11 - PATTERNS, RELATIONSHIPS, AND FUNCTIONS
|
All students will develop an understanding of patterns,
relationships, and functions and will use them to represent and
explain real-world phenomena.
|
Standard 11 - Patterns, Relationships, and Functions - Grades 3-4
Overview
The development of pattern-based thinking, using patterns to
analyze and solve problems, is an extremely powerful tool for doing
mathematics, and leads in later grades to an appreciation of how
functions are used to describe relationships. The key components of
pattern-based thinking at the early grade levels, as identified
in the K-12 Overview, are recognizing, constructing, and extending
patterns, categorizing and classifying objects
discovering rules, and working with input-output
situations.
In grades 3 and 4, students begin to learn the importance of
investigating a pattern in an organized and systematic way. Many of
the activities at these grade levels focus on creating and using
tables as a means of analyzing and reporting patterns. In addition,
students in these grades begin to move from learning about patterns to
learning with patterns, using patterns to help them make sense of the
mathematics that they are learning.
Students in grades 34 continue to construct, recognize, and
extend patterns. At these grade levels, pictorial or symbolic
representations of patterns are used much more extensively than in
grades K-2. In addition to studying patterns observed in the
environment, students should use manipulatives to investigate what
happens in a pattern as the number of terms is extended or as the
beginning number is changed. Students should also study patterns that
involve multiplication and division more extensively than in earlier
grades. Students continue to investigate what happens with patterns
involving money, measurement, time, and geometric shapes. They should
use calculators to explore patterns.
Students in these grades continue to categorize and classify
objects. Now categories can become more complex, however, with
students using two (or more) attributes to sort objects. For example,
attribute shapes can be described as red, large, red and large, or
neither red nor large. Classification of naturally-occurring objects,
such as insects or trees, continues to offer an opportunity for
linking the study of mathematics and science.
Students in grades 3 and 4 are more successful in playing
discover a rule games than younger students and can work with a
greater variety of operations. Most students will still be most
comfortable, however, with one-step rules, such as multiplying by
3 or dividing by 4.
Third and fourth graders also continue to work with input-output
situations. While they still enjoy putting these activities in a
story setting (such as Max the Magic Math Machine which takes
in numbers and hands out numbers according to certain rules), they are
now able to consider these situations in more abstract contexts.
Students at this age often enjoy pretending to be the machine
themselves and making up rules for each other.
In grades 3 and 4, then, students expand their study of patterns to
include more complex patterns based on a greater variety of numerical
operations and geometric shapes. They also work to organize their
study of patterns more carefully and systematically, learning to use
tables more effectively. In addition, they begin to apply their
understanding of patterns to learning about new mathematics concepts,
such as multiplication and division.
Standard 11 - Patterns, Relationships, and Functions - Grades 3-4
Indicators and Activities
The cumulative progress indicators for grade 4 appear below in
boldface type. Each indicator is followed by activities which
illustrate how it can be addressed in the classroom in grades 3 and
4..
Building upon knowledge and skills gained in the preceding grades,
experiences in grades 3-4 will be such that all students:
1. Reproduce, extend, create, and describe
patterns and sequences using a variety of materials.
- Students make a pattern book that shows
examples of patterns in the world around them.
- Students use pattern blocks, attribute blocks, cubes,
links, buttons, beans, toothpicks, counters, crayons, magic markers,
leaves, and other objects to create and extend patterns. They might
describe a pattern involving the number of holes in buttons, the
number of sides in a geometric figure, the shape or the thickness of
objects.
- Students use sequences of letters or numbers to identify
the patterns they have created.
- Students investigate the sum of the dots on opposite faces
of an ordinary die and find they always add up to 7.
- Students solve twodimensional attribute block
patterns where, for instance, each column is a different shape and
each row is a different color. They should be able to choose the
block that fills in the missing cell in such patterns.
- Students count by 2, 3, 4, 5, 6, 10 and 12 on a number
line, on a number grid, and on a circle design.
- Students begin with numbers between 50 and 100 and count
backwards by 2, 3, 5, or 10.
- Students create patterns with the calculator: They enter
any number such as 50, and then repeatedly add or subtract 1 or 2 or 3
etc. If, for example, they enter 50+1=== ... , the calculator will
automatically repeat the function and display 51, 52, 53, 54, ... .
Some calculators may need to have the pattern entered twice:
50+1=+1=== ... . Others may need 1++ 50=== ... .
- Students begin with a number less than 10, double it, and
repeat the doubling at least five times. They record the results of
each doubling in a table and summarize their observations in a
sentence.
- Students read Anno's Magic
Seeds by Mitsumasa Anno. In it, a wizard gives Jack two seeds and
tells him that if he eats one, he won't be hungry for a year and
if he plants the other one, two new seeds will be formed. Jack
continues in this way for awhile and then tries other schemes that
produce even more new seeds. The students work in groups to make
charts and tables to show how many seeds Jack has at given points in
time. As an individual assessment assignment, students are asked to
find how many seeds Jack has after ten years using one of the
discovered patterns and to support their answers in writing and with
tables.
- Students supply the missing numbers on a picture of a ruler
which has some blanks. Then they explore how to find the missing
numbers between any two given numbers on a number line. They extend
this to larger numbers; they might label each of five intervals from
200 to 300 or each of four intervals from 1,000 to 2,000.
- Students investigate number patterns using their
calculators. For example, they might begin at 30, repeatedly add 6,
and record the first 10 answers, making a prediction about what the
calculator will show before they hit the equals key. Or they might
begin at 90 and repeatedly subtract 9.
2. Use tables, rules, variables, open sentences, and
graphs to describe patterns and other relationships.
- As a regular assessment
activity, done during the year whenever new numerical operations have
been explored, students fill in guess my rule tables like those
shown below. Sometimes they are given the rule and sometimes they are
asked to find the rule.
- Students describe the pattern illustrated by the numbers in
a table by using words (e.g., twice as much as) and then represent it
with symbols in an open sentence
(
 = 2 x = 2 x  ). ).
- On a coordinate grid, students plot coordinate pairs
consisting of a number and the product of the number times 3. They
join them with a line, making a line graph. They relate this to a
table, and write the rule as an expression involving a variable, such
as 3 x
 . .
- Students repeatedly add (or subtract) multiples of 10 to
(from) a 3-digit starting number. They describe the pattern orally and
write it symbolically as, for example, 357, 337, 317, 297, ... .
- Students work in groups to solve problems that involve
organizing information in a table and looking for a pattern. For
example, If you have 12 wheels, how many bicycles can you
make? How many tricycles? How many bicycles and tricycles
together? Using objects or pictures, children make models and
organize the information in a table. They discuss whether they have
looked at all of the possibilities systematically and describe in
words the patterns they have found. They write about the patterns in
their journals and, with some assistance, develop some symbolic
notation (e.g., 2 wheels for each bike and 3 wheels for each trike to
get 12 wheels all together might become 2xB + 3xT = 12).
3. Use concrete and pictorial models to explore the
basic concept of a function.
- Students use buttons with two or four holes and describe
how the total number of holes is related to the number of buttons.
- Students use multilink cubes or base ten blocks to build
rectangular solids. They count how many cubes tall their structure
is, how many cubes long it is, and how many cubeswide it is. Then
they count the total number of cubes in their structure. They record
all of this information in a table and look for patterns.
- Students take turns putting numbers into Max the Magic
Math Machine, reading what comes out, and finding the rule that
tells what Max is doing to each number. A student acts as Max each
time. Appropriate rules to use in grades 3 and 4 involve
multiplication and division.
4. Observe and explain how a change in one
physical quantity can produce a corresponding
change in another.
- Students use cubes to build a
one-story "house" and count the number of cubes used. They
add a story and observe how the total number of cubes used changes.
They explain how changing the number of stories changes the number of
cubes used to build the house.
- Students measure the temperature of a cup of water with ice
cubes in it every fifteen minutes over the course of a day. They
record their results (time passed and temperature) in a table and plot
this information on a coordinate grid to make a broken line
graph. They discuss how the temperature changes over time and why.
- Students plant seeds in vermiculite and in soil. They
observe the plants as they grow, measuring their height each week and
recording their data in tables. They examine not only how the height
of each plant changes as time passes but also whether the seeds in
vermiculite or soil grow faster.
5. Observe and recognize examples of patterns,
relationships, and functions in other disciplines and
contexts.
- Students go on a scavenger hunt for
patterns around the classroom and the school. They are given a list
of verbal descriptions of specific patterns to look for, such as a
pattern using squares or an ABAB pattern. They use
cameras to make photographs of the patterns that they find.
- Students read The Twelve Days of Summer by
Elizabeth Lee O'Donnell and Karen Lee Schmidt. Using the same
pattern as the song The Twelve Days of Christmas, the authors
tell the story of a young girl on vacation by the ocean. On the first
day, she sees "a little purple sea anemone," on the eighth,
"eight crabs ascuttling," and so on. Since she sees
everything that she has previously seen on every succeeding day, the
book offers the obvious question How many things did the little
girl see today?
- Students learn about the different time zones across the
country. They describe the number patterns found in moving from east
to west, and vice versa.
- Students read books such as Six Dinner Sid by Inga
Moore or The Greedy Triangle by Marilyn Burns. They explore
the patterns and relationships found in these books.
- Students study patterns in television programming. For
example, they might look at the number of commercials on TV in an hour
or how many cartoon shows are on at different times of the day. They
discuss the patterns that they find as well as possible reasons for
those patterns.
6. Form and verify generalizations based
on observations of patterns and relationships.
- Students measure the length of one side of a square in
inches. They find the perimeter of one square, two squares (not
joined), three squares, and so on. They make a table of values and
describe a rule which relates the perimeter to the number of squares.
They predict the perimeter of ten squares.
- Students use their calculators to find the answers to a
number of problems in which they multiply a two-digit number by 10,
100, or 1000. Looking at their answers, they develop a
"rule" that they think will help them do this type of
multiplication without the calculator. They test their rule on some
new problems and check whether their rule works by multiplying the
numbers on the calculator.
References
-
Anno, Mitsumasa. Anno's Magic Seed. New
York: Philomel Books, 1995.
Burns, Marilyn. The Greedy Triangle. New York:
Scholastic Inc., 1994.
O'Donnell, Elizabeth Lee, and Karen Lee Schmidt. The
Twelve Days of Summer. Morrow Junior Books, 1991.
Moore, Inga. Six Dinner Sid. New York: Simon and
Schuster, 1993.
On-Line Resources
-
http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/
The Framework will be available at this site during
Spring 1997. In time, we hope to post additional resources
relating to this standard, such as grade-specific activities submitted
by New Jersey teachers, and to provide a forum to discuss the
Mathematics Standards.
|
 = 2 x
= 2 x 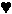 ).
).