Students can develop a strong understanding of algebraic concepts and processes from consistent experiences in classroom activities where a variety of manipulatives and technology are used. The key components of this understanding in algebra, as identified in the K-12 Overview, are: patterns, unknown quantities, properties, functions, modeling real-world situations, evaluating expressions and solving equations and inequalities.

Students in grades 7 and 8 continue to explore algebraic concepts in an informal way. By using physical models, data, graphs, and other mathematical representations, students learn to generalize number patterns to model, represent, or describe observed physical patterns, regularities, and problems. These informal explorations help students gain confidence in their ability to abstract relationships from contextual information and use a variety of representations to describe those relationships. Manipulatives such as algebra tiles provide opportunities for students with different learning styles to understand algebraic concepts and manipulations. Graphing calculators and computers enable students to see the behaviors of functions and study concepts such as slope.

Students need to continue to see algebra as a tool which is useful in describing mathematics and solving problems. The algebraic experiences should develop from modeling situations where students gather data to solve problems or explain phenomena. It is important that all concepts are presented within a context, preferably one meaningful to students, rather than through traditional symbolic exercises. Once a concept is well-understood, the students can use traditional problems to reinforce the algebraic manipulations associated with the concept.

Many activities which are used in earlier grades should be revisited as students become more sophisticated in their use of algebra. At the same time, activities used in later grades can be incorporated on an informal basis. For example, students in earlier grades might have gathered the heights and armspans and attempted to generalize the relationship between them in words. As students became familiar with the rectangular coordinate system, they might have generalized the relationship using a scatterplot and fitting a line to the data. In seventh and eighth grade, students might be taught how to find the medianmedian line to determine the line of best fit and use that line to solve problems. In later grades, when students have learned to find the slope of a line through two points symbolically, they can determine the equation of the median-median line. (The median-median line, available on many calculators which have statistics capabilities, is found by dividing the data points on the x-y plane into three equal sets, grouped by x-value, finding a single point for each set whose coordinates are the medians of the respective coordinates of the points in the set, connecting the first and third points by a straight line, and shifting this line 1/3 of the way toward the second point.)

Students should have numerous opportunities to develop an understanding of the relationship between a function and its graph. A limited number of functions should be plotted by hand, but students should also use technology to graph functions. While linear relationships should be the focus, inequalities and nonlinear functions should be explored as well. Students should develop an understanding of the relationship between solutions of equations and graphs of functions. For example, the solution of the equation 3 x - 4 = 5 can be found by plotting y = 3x - 4, tracing along the function until a y-value of 5is found, and then determining the corresponding x-value. Students should develop the ability to find solutions using the trace function of graphing calculators and computer graphing programs and discuss how it assists in solving equations. They should also have opportunities to use spreadsheets as a method for representing and solving problems.

Students should be able to evaluate expressions using all forms of real numbers when calculators are available. They should have developed an understanding of the importance of the algebraic order of operations and be able to correctly evaluate expressions using it. It is imperative that students understand that they cannot blindly accept answers produced on the calculator. They should recognize that a standard fourfunction calculator does not use the standard order of operations. They should recognize that even with a scientific calculator, operations such as the division of two binomial quantities requires the use of parentheses.

Students should refine their ability to solve simple linear equations (i.e., ax+b=cx + d). Students may continue to use informal, concrete, and graphic methods but should begin to link these methods to more formal symbolic methods. As students have opportunities to explore interesting problems, applications, and situations, they need to be encouraged to reflect on their explorations and summarize concepts, relationships, processes, and facts that have emerged from their discussions. Developing a suitable notation to describe these conclusions leads naturally to a more formal, more symbolic view of algebra.

The cumulative progress indicators for grade 8 appear below in boldface type. Each indicator is followed by activities which illustrate how it can be addressed in the classroom in grades 7 and 8.

Building upon knowledge and skills gained in the preceding grades, experiences in grades 7-8 will be such that all students:

5. Understand and use variables, expressions, equations, and inequalities.

• Students make a model of the relationship between Celsius and Fahrenheit temperatures. They represent the relationship as a formula, and check the formula against two known data points - 0 degrees Centigrade = 32 degrees Fahrenheit and 100 degrees Centigrade = 212 degrees Fahrenheit. Students use their formula to convert between Celsius and Fahrenheit temperatures.

• Students examine the following situation, making a table for the first few months to gain an understanding of the pattern involved in the problem.

  Juanita opened a checking account and deposited $500. She works as a parttime engineer's assistant in a local firm and will receive a check for $130 on the 1st and 15th of each month. She intends to take $40 from each paycheck for cash expenses and then deposit the remainder. On the 15th of each month, she will write a check for $220 to cover the cost of her car payment.

  The students develop an equation that describes how much money is in the account on the 1st and the 15th of each month. They use their equation to determine the amount for various months in the future as well as to find out when Juanita will overdraw the account. Students use their equations and the information they have found to write a letter to Juanita explaining why her plan is not financially sound and what she might do to correct it.

6. Represent situations and number patterns with concrete materials, tables, graphs, verbal rules, and standard algebraic notation.

• The seventh grade is preparing for a skiing trip. The interdisciplinary team has decided to integrate the planning for the trip into all the courses. One of the items being discussed in math class is the number of buses that will be required. Since the actual number of people is not yet determined, the situation is best modeled with variables and unknowns. Knowing that each bus holds 35 people, students develop a table based on 5 or 6 different numbers of people on the trip, in an attempt to find a pattern. Some students who require more concrete operations to develop a sense of the pattern use unit cubes and decimal rods to represent the situation with different numbers of people. The group works together to develop a graph based on their findings. The discussion begins with one person suggestinggraphing the points (35,1), (70,2), and (105,3) and then connecting them with a straight line. The teacher does this (in a way that can be readily erased later) and asks the class if there is any problem with this solution. More discussion leads to understanding that the graph would be made up of discrete points since there cannot be fractions of people and the graph would not be a straight line but a series of steps 35 people long and going up by 1 bus. Students are able to verbalize the rule but are curious as to how it would be represented symbolically. The teacher shows them the symbol for the step function, _x_.

• Students construct squares on each side of right triangles on their geoboards, then find the area of each square. They record their results in a table and look for a pattern, leading them to "discover" the Pythagorean Theorem.

7. Use graphing techniques on a number line to model both absolute value and arithmetic operations.

• Students use a graphic representation of the mapping resulting from a multiplication by a negative number (such as 2 as shown below) to explain why the order of the inequality reverses when both sides are multiplied by that negative number.
  

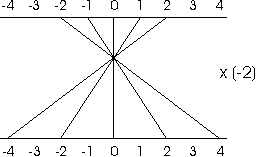
  They explain that while the original sequence of inputs is ascending {2,1,0,1,2}, the images are descending {4,2,0,2,4}.

• Presented with an absolute value equation such as | x - 5 | < 3, the students use the idea that this means identifying all the points which are 3 units or less from 5. They represent the solution set with dots at 2 and 8 and a line connecting them.

• Students represent multiplication of integers on the number line as repeated addition. They use the idea that 3 × 4 is 4 + 4 + 4, and, on the number line, it would be represented by three segments, each four units in length, placed end to end starting at zero. The students write in their journals how they would picture 3 × (4). After reviewing their responses and clarifying concerns, they discuss that (3) × (4) would be the opposite of 3 × (4).

8. Analyze tables and graphs to identify properties and relationships.

• Students work on the handshake problem (How many handshakes would there be in a group of 25 people if each person shook hands with every other person exactly once?) by considering smaller groups of people and recording the results for these smaller groups in a table. Students identify the pattern and develop an expression which relates the number of people to the number of handshakes. Some students place 25 points on paper, forming a polygon, and begin drawing the segments which connect the points to generate a geometric pattern.

• Students explore the relationship between the number of sides of a regular polygon and the total number of diagonals that can be drawn in that polygon. They organize their work in a table, graph the data, and write a general rule that could be applied to the nth polygon. They connect this problem to the handshake problem.

• Students work in groups on the following EWT-like problem from the Mathematics Instructional Guide published by the New Jersey State Department of Education:

  The Hiking Club takes a long walk every Saturday. If they hike at a constant speed, which graph shows the relationship between the distance they cover and the time it takes them to cover the distance?

  

• Students perform an experiment in which they determine how far a toy car rolls from the end of a ramp as the height of the ramp changes. They gather the data, make a scatterplot, and fit a line to the data using the medianmedian line method. They use the graph to answer additional questions regarding the situation. Some students find the slope and y-intercept of the graph and use these to determine the equation of the line. The class then uses the equation to check its answers to the questions.

9. Understand and use the rectangular coordinate system.

• Students draw the quadrilateral ABCD, where the coordinates of the vertices are A(3,2), B(4,7), C(2,3), and D(5,6). They produce the figure that results from a size change of 1/2 and then slide that quadrilateral left 3 units and down 5.

• Students understand that the point (5,3) is the intersection of two lines which have the equations x=5 and y=3. They can identify quickly lines with equations such as x=5 and y=3. They can identify the half planes and intersections of half planes identified by inequalities such as x>5 and y< 3.

• Students study the relationship between perimeters and areas of rectangles. Some students keep the perimeter constant and study the changes in area while others keep the area constant and study the changes in perimeter. Both groups plot their results as graphs and look for patterns.

• Students use squares or grid paper to study the relationship between the radius of a circle and its area (found by counting squares on centimeter grid paper). They graph their data and use it to predict the area of a circle of radius r.

• Students play Green Globs on the computer, entering equations and trying to hit as many globs as possible with them.

10. Solve simple linear equations using concrete, informal, and graphical methods, as well as appropriate paper-and-pencil techniques.

• Presented with a picture of a balance scale showing objects with unknown weights on both sides as well as known weights (e.g., 3x + 12 = 7x + 4), students identify the standard algebraic equation related to the picture, describe in words how it would be solved using the concrete objects on the balance scale, and record their actions symbolically.

• Students use algebra tiles to solve an equation like 3(2x + 5) = 21. They first place 21 units on the right and three groups of two strips and five units on the left. They then note that this is the same as saying 6 strips and 15 units balance 21 units (6x + 15 = 21). Then they take 15 units off both sides, leaving 6 strips balanced with 6 units (6x = 6). They conclude that one strip must equal one unit (x = 1).

• As part of a regular exam, students write a verbal explanation describing the relationship between the function y=2x+4, its graph, and the equation 2=2x+4.

11. Explore linear equations through the use of calculators, computers, and other technology.

• The students perform an experiment to answer the question about how long it would take a wave to go around Veterans' Stadium. They gather data by timing waves done by a various numbers of people, plot the data, and determine the line of best fit using the medianmedian line method. They determine the number of people that could sit around Veterans Stadium, but they discover that, unlike the previous data sets, they cannot use the graph to answer the question directly. The teacher explains that they need to determine an equation for the line. She has the students investigate functions of the form y=mx+b using a graphing calculator in order to develop the idea that m represents the slope and b represents the y-intercept.

• Using a motion detector connected to a computer or graphing calculator, the teacher has students walk so that the distance from the detector plotted against time is a straight line. The teacher gives directions to students such as: Walk so that the line has a positive slope, Walk so that the slope is steeper than the last line, Walk so that the line has a slope of 0, or Walk so that the line has a negative slope.

12. Investigate inequalities and nonlinear equations informally.

• Presented with the information that the Cape MayLewes Ferry has space for 20 cars, and a bus takes up the space of 3 cars, students are asked to draw a graph which represents how many cars and how many buses can be taken across on one trip. Students use variables to represent the unknowns (x for cars and y for buses) and develop the inequality x+3y < 20 as a model for the situation. Recognizing that the solutions have to be whole numbers, they identify the points whose coefficients are non-negative integers and in the first quadrant on or below the line.

• Students use a motion detector, connected to a calculator or computer, to record the motion of a ping-pong ball tossed by a small catapult. The motion detector is on the floor below the trajectory of the ball. Students note that the graph of distance against time is not linear. They experiment with different initial velocities and different release points to see how these affect the graph.

13. Draw freehand sketches of, and interpret, graphs which model real phenomena.

• Students are asked to draw a sketch of the graph which would describe a person's distance off the ground during a ride on a ferris wheel which had a radius of 60 feet. Some students just draw a curve that looks similar to a sine curve. Others put more detail into their drawing showing the step function behavior which occurs as people get on and get off and that there are limited revolutions permitted.

• Presented with a graph showing the population of frogs in a local marsh over the past ten years, students generate hypotheses for why the curve has the shape it does. They check their hypotheses by talking with a local biologist who has studied the marsh over this time period.

References

New Jersey State Department of Education. Mathematics Instructional Guide. D. Varygiannes, Coord. Trenton: 1996.

Software

Green Globs and Graphing Equations. Sunburst Communications.

On-Line Resources

http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/

The Framework will be available at this site during Spring 1997. In time, we hope to post additional resources relating to this standard, such as grade-specific activities submitted by New Jersey teachers, and to provide a forum to discuss the Mathematics Standards.