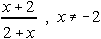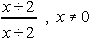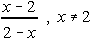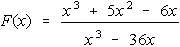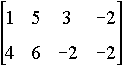Students can develop a strong understanding of algebraic concepts and processes from consistent experiences in classroom activities where a variety of manipulatives and technology are used. The key components of this understanding in algebra, as identified in the K-12 Overview, are: patterns, unknown quantities, properties, functions, modeling real-world situations, evaluating expressions, and solving equations and inequalities.

With the foundation developed in the K8 program, students should be able to be successful in most secondary algebra programs. However, instructional strategies should continue to focus on algebra as a means for representing and modeling real situations and answering questions about them. The traditional methods of teaching algebra have been likened to teaching a foreign language, focusing on grammar and not using the language in real conversation. Algebra courses and programs must encourage students to "speak the language" as well as use "proper grammar."

Algebraic understanding is necessary for all students regardless of the structure of the 912 program. Students in mathematics programs from technical/basic through college preparatory programs should learn a common core of algebra, with the remainder of the program based on their particular needs. All students should learn the same basic ideas. All students benefit from instructional methods which provide context for the content. Such an approach makes algebra more understandable and motivating.

Techniques for manipulating algebraic expressions remain important, especially for students who may continue into a calculus program. These can be woven into the curriculum or they might all be combined into separate courses labeled "algebra" taken by students who intend to pursue a mathematicsrelated career. No matter how this instruction is organized, however, instruction must produce students who understand the logic and purposes of algebraic procedures.

Students should be comfortable with evaluating expressions and with solving equations and inequalities, by whatever means they find most appropriate. They should understand the relationship between the graphs of functions and their equations. Prior to high school, they have focused predominantly on linear functions. In high school, students should gain more familiarity with nonlinear functions. They should develop the ability to solve equations and inequalities using appropriate paperandpencil techniques as well as technology. For example, they should be able to understand and solve quadratic equations using factoring, the quadratic formula, and graphing, as well as with a graphing calculator. They should recognize that the methods they use can be generalized to be used when functions look different but are actually composite functions using a basic type (e.g., sin² x + 3 sin x + 2 = 0 is like x² + 3x + 2 = 0); this method is sometimes called "chunking." This use of patterns to note commonalities among seemingly different problems is an important part of algebra in the high school.

Algebraic instruction at the secondary level should provide the opportunity for students to revisit problems. Traditional school problems leave students with the impression that there is one right answer and that once an answer is found there is no need to continue to think about the problem. Since algebra is the language of generalization, instruction in this area should encourage students to ask questions such as Why does the solution behave this way? They should develop an appreciation of the way algebraic representation canmake problems easier to understand. Algebraic instruction should be rich in problems which are meaningful to students.

Algebra is the gatekeeper for the future study of mathematics and of science, social sciences, business, and a host of other areas. In the past, algebra has served as a filter, screening people out of these opportunities. For New Jersey to be part of a global society, it is important that 912 instruction in algebra play a major role in the culminating experiences of a twelveyear program that opens these gates for all.

The cumulative progress indicators for grade 12 appear below in boldface type. Each indicator is followed by activities which illustrate how it can be addressed in the classroom in grades 9, 10, 11, and 12.

Building upon knowledge and skills gained in the preceding grades, experiences in grades 9-12 will be such that all students:

14. Model and solve problems that involve varying quantities using variables, expressions, equations, inequalities, absolute values, vectors, and matrices.

• Students take data involving two variables in an area of interest to them from the World Almanac, construct a scatterplot, and predict the type of equation or function which would best model the data. They use a computerized statistics package or a calculator to fit a function of this type to the data. They choose from linear, quadratic, exponential or logarithmic methods and discuss how well the model fits as well as the limitations.

• Students use matrices to represent tabular information such as the print runs below for each of two presses owned by a book company. They then calculate a third matrix that indicates the growth in production of each press from 1987 to 1988 and discuss the meaning of the data contained in it.

  1988	Textbooks	Novels	Nonfiction
  Press 1	250,000	125,000	312,000
  Press 2	60,000	48,000	90,000

  1987	Textbooks	Novels	Nonfiction
  Press 1	190,000	100,000	140,000
  Press 2	45,000	60,000	72,000

  Some students perform the operations by hand while others explain how they would do it and then use their graphing calculator or a spreadsheet, or write a computer program, which accomplishes the task.

• Students use vectors to determine the path of a plane that was flying due north at 300 miles per hour while a wind was blowing from the southwest at a speed of 15 miles per hour. Students draw a diagram and use an algebraic approach.

• Students work in groups on the following HSPT-like problem from the Mathematics Instructional Guide published by the New Jersey State Department of Education:

  As you ride home from a football game, the number of kilometers you are away from home depends (largely) on the number of minutes you have been riding. Suppose that you are 13 km from home when you have been riding for 10 minutes, and 8 km from home when you have been riding for 15 minutes. (Assume that the distance varies linearly with time.) Make a graph with the vertical axis representing distance home and the horizontal axis representing time. Label your graph. Plot the data given as two points on your graph. About how long did it take (on average) to travel 1 km? About how far was the football game from your home? Explain your answer.

• Students work through the Breaking the Mold lesson that is described in the Introduction to this Framework. They use a science experiment involving growing a mold to learn about exponential growth of populations and compound interest.

• Students work through the What's My Line unit that is described in the Keys to Success chapter of this Framework. In this unit, students find a linear relationship between the length of a person's thigh bone and his height, and use this to estimate the height of a person whose thigh bone has been found.

• Students work through the Ice Cones lesson that is described in the First Four Standards of this Framework. In this lesson, an ice-cream vendor's problem of folding a circle into a cone of maximum volume is solved by expressing the volume as a function which is then displayed on an graphing calculator.

15. Use tables and graphs as tools to interpret expressions, equations, and inequalities.

• On a test, students are asked to determine the truth value of the statement "log x > 0 for all positive real numbers x." One student remembers that log x is the exponent to which 10 must be raised to get x, and to get a number less than 1 would require a negative exponent. Another student picks some trial points, develops a chart of the points and their logarithms and discovers that when x < 1, log x < 0. A third student graphs the function on his graphing calculator and sees that when x < 1, the graph of log x is below the xaxis.

• Faced with the problem of solving the inequality x² 3x < 4, some students use the equation x² 3x 4 = 0 to determine the boundary points of the interval that satisfies the inequality. They factor the equation and find that these endpoints are 1 and 4. They place dots on the number line at those points, since they know the endpoints are included in the solution set, and then substitute 0 for x in the original inequality. When they find that the resulting statement is true, they shade the interval connecting the two points to obtain their solution -1 < x < 4. Some students determine the endpoints in the same way but roughly sketch a graph of the parabola y =x² - 3 x - 4 and determine that since the inequality was < , the problem was asking when the parabola was below the xaxis. Their graph indicates that this happens in the region between the two endpoints. Other students used their graphing calculators to graph the function x² 3x and used the trace function to determine when the graph was on or below the line y=4. All students, however, are able to use all these methods to solve the problem.

16. Develop, explain, use, and analyze procedures for operating on algebraic expressions and matrices.

• Students use algebra tiles to develop procedures for multiplying binomials and factoring trinomials. They summarize these procedures in their math notebooks, applying them to the solution of real-world problems. They work through the Making Rectangles lesson described in the First Four Standards of this Framework, where they discuss which combinations of tiles can be formed into rectangles, and relate this question to factoring trinomials.

• Students work in groups on the following HSPT-like problem from the Mathematics Instructional Guide (p. 7-153) published by the New Jersey State Department of Education:

  Which of the following is NOT another name for 1?

  A.			B.
  C.			D.

• After many experiences with trying to determine appropriate windows for graphing functions on computers or graphing calculators, students develop an understanding of the need to know what the general behavior of a function will be before they use the technology. Students are then asked to explain how they could determine the behavior of the graph of the function below.
  

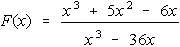
  Students factor the numerator and denominator to determine the values which make them zero and use those values to identify the xintercepts and vertical asymptotes, respectively. They discuss the fact that the factors x and x+6 appear in both places and lead to a removable discontinuity represented by a hole in the graph. They discuss the end behavior of the function as approaching y = 1 and the behavior near the vertical asymptote of x = 6.

• Following a unit on combinations and binomial expansion, students make a journal entry discussing the power of Pascal's triangle in expanding powers of binomial expressions as compared to the traditional multiplication algorithm.

17. Solve equations and inequalities of varying degrees using graphing calculators and computers as well as appropriate paperandpencil techniques.

• Students are asked to find the solutions to 2^x = 3x². Some students use a spreadsheet to develop a table of values. Once they find an interval of length 1 which contains a solution, they refine their numbers to develop the answer to the desired precision. Otherstudents graph both y = 2^x and y = 3x² using graphing calculators or computers and use the trace function to determine where they intersect. Other students graph the function y = 3 x² - 2^x and use the trace function to find the zeroes. Other students enter the function in their graphing calculator and check the table of values.

• As a portion of a final assessment, students are given one opportunity to place a cup which is supported 6 inches off the ground in such a position as to catch a marble rolled down a ramp. They perform the roll without the cup to locate the point where the marble strikes the ground. They measure the height of the end of the ramp above the ground and the distance from the point on the ground directly beneath the end of the ramp to the point where the marble struck the ground. They generate the quadratic function which models the path of the marble. Several students use different methods to ensure they have the correct function. Then they decide where they will have to place the cup by substituting 6 for the function value and determining the corresponding xvalue. Students solve the equation using the quadratic formula, and the trace function on a graphing calculator, and proceed to place the cup and roll the ball only when the solutions produced by all of the methods agree.

18. Understand the logic and purposes of algebraic procedures.

• Students use matrices as arrays of information, so that the matrix below, for example, is recognized as representing the four vertices {(1,4), (5,6), (3, - 2), (- 2, - 2)} of a polygon. Reducing the polygon by 1/2 can then be represented by multiplying the matrix by the scalar 1/2 and moving the polygon to the right one unit can be represented by adding to it a 2 x 4 matrix whose top row consists of 1s and its bottom row of 0s.
  

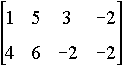
• Students read Mathematics in the Time of the Pharaohs by Richard Gillings to understand the development of Egyptian mathematics including computational procedures for dealing with direct and inverse proportions, linear equations, and trigonometric functions.

• Students explain in their journals how the identity matrix is like the number one.

19. Interpret algebraic equations and inequalities geometrically, and describe geometric objects algebraically.

• Students investigate the characteristics of the linear functions. For example: In y = kx, how does a change in k affect the graph? In y = mx + b, what does b do? Does k in the first equation serve the same purpose as m in the second? Students use the graphing calculator to investigate and verify their conclusions.

• Students investigate the effects of a dilation and/or a horizontal or vertical shift on the coefficients of a quadratic function. For example: How does moving the graph up 3 units affect the equation? How does moving the graph right 3 unites affect the equation?

• Students look at the effects of changing the coefficients of a quadratic equation on the graph. For example: How is the graph of y = 4x² different from that of y = x²? How is y = .2x² different from y = x²? How are y = x² + 4, y = x² 4, y = x² 4x, and y = x²4x + 4 each different from y = x²? Students use graphing calculators to look at the graphs and summarize their conjectures in writing. They also work through the Building Parabolas lesson described in the First Four Standards of this Framework, where students discuss the general equation of a parabola and use Green Globs software to find equations of parabolas that pass through specified points.

• Students study the behavior of functions of the form y = axⁿ. They investigate the effect of a on the curve and the characteristics of the graph when n is even or odd. They use the graphing calculator to assist them and write a sentence summarizing their discoveries.

• Students are asked to consider the following situation:

  A landscaping contractor uses a combination of two brands of fertilizers, each containing a different amount of phosphates and nitrates. In a package, brand A has 4 lb. of phosphates and 2 lb. of nitrates. Brand B contains 6 lb. of phosphates and 5 lb. of phosphates. On her current job, the lawn requires at least 24 lb. of phosphates and at least 16 lb. of nitrates. How much of each fertilizer does the contractor need?

  Students represent the given conditions as inequalities and use the intersection of their regions as the set of feasible answers.

• Students recognize that solving two equations simultaneously like 2x+y=5, 4x-y=1 amounts to finding the point of intersection of the two lines with equations y=-2x+5, y=4x-1. Similarly they recognize that solving a quadratic equation like 2x² -3x-5=0 amounts to finding where the parabola y=2x²-3x-5 crosses the x-axis.

References

Gillings, Richard. Mathematics in the Time of the Pharoahs.

New Jersey State Department of Education. Mathematics Instructional Guide. D. Varygiannes, Coord. Trenton: 1996.

Software

Green Globs and Graphing Equations. Sunburst Communications.

On-Line Resources

http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/

The Framework will be available at this site during Spring 1997. In time, we hope to post additional resources relating to this standard, such as grade-specific activities submitted by New Jersey teachers, and to provide a forum to discuss the Mathematics Standards.