The five major themes of discrete mathematics, as discussed in the K-12 Overview, are systematic listing, counting, and reasoning; discrete mathematical modeling using graphs (networks) and trees; iterative (that is, repetitive) patterns and processes; organizing and processing information; and following and devising lists of instructions, called "algorithms," and using them to find the best solution to real-world problems.

Despite their formidable titles, these five themes can be addressed with activities at the 7-8 grade level which involve both the purposeful play and simple analysis suggested for elementary school students and experimentation and abstraction appropriate at the middle grades. Indeed, teachers will discover that many activities that they already are using in their classrooms reflect these themes. These five themes are discussed in the paragraphs below.

The following discussion of activities at the 7-8 grade levels in discrete mathematics presupposes that corresponding activities have taken place at the K-6 grade levels. Hence 7-8 grade teachers should review the K-2, 3-4, and 5-6 grade level discussions of discrete mathematics and might use activities similar to those described there before introducing the activities for this grade level.

Students in 7th and 8th grade should be able to use permutations and combinations and other counting strategies in a wide variety of contexts. In addition to working with permutations, where the order of the items is important (see Grades 5-6 Overview and Activities), they should also be able to work with combinations, where the order of the items is irrelevant. For example, the number of different three digit numbers that can be made using three different digits is 10x9x8 because each different ordering of the three digits results in a different number. However, the number of different pizzas that can be made using three of ten available toppings is (10x9x8)/(3x2x1) because the order in which the toppings are added is irrelevant; the division by 3x2x1 eliminates the duplication.

An important discrete mathematical model is that of a network or graph, which consists of dots and lines joining the dots; the dots are often called vertices (vertex is the singular) and the lines are often called edges. (This is different from other mathematical uses of the term "graph.") Graphs can be used to represent islands and bridges, or buildings and roads, or houses and telephone cables; wherever a collection of things are joined by connectors, the mathematical model used is that of a graph. Students in the 7th and 8th grades should be able to use graphs to model situations and solve problems using the model. For example, students should be able to use graphs to schedule a school's extracurricular activities so that, if at all possible, no one is excluded because of conflicts. This can be done by creating a graph whose vertices are the activities, with two activities joined by an edge if they have a person in common, so that the activities should be scheduled for different times. Coloring the vertices of the graph so that adjacent vertices have different colors, using a minimum number of colors, then provides an efficient solution to the scheduling problem - a separate time slot is needed for each color, and two activities are scheduled for the same time slot if they have the same color.

Students can recognize and work with iterative and recursive processes, extending their earlierexplorations of repetitive patterns and procedures. In the 7th and 8th grade, they can combine their understanding of exponents and iteration to solve problems involving compound interest with a calculator or spreadsheet. Topics which before were viewed iteratively - arriving at the present situation by repeating a procedure n times - can now be viewed recursively - arriving at the present situation by modifying the previous situation. They can apply this understanding to Fibonacci numbers, to the Tower of Hanoi puzzle, to programs in Logo, to permutations and to other areas.

Students in the 7th and 8th grades should explore how codes are used to communicate information, by traditional methods such as Morse code or semaphore (flags used for ship-to-ship messages) and also by current methods such as zip codes. Students should investigate and report about various codes that are commonly used, such as binary codes, UPCs (universal product codes) on grocery items, and ISBN numbers on books. They should also explore how information is processed. A useful metaphor is how a waiting line or queue is handled (or "processed") in various situations; at a bank, for example, the queue is usually processed in first-in-first-out (FIFO) order, but in a supermarket or restaurant there is usually a pre-sorting into smaller queues done by the shoppers themselves before the FIFO process is activated.

In the 7th and 8th grade, students should be able to use algorithms to find the best solution in a number of situations - including the shortest route from one city to another on a map, the cheapest way of connecting sites into a network, the fastest ways of alphabetizing a list of words, the optimal route for a class trip (see the Short-Circuiting Trenton lesson in the Introduction to this Framework), or optimal work schedules for employees at a fast-food restaurant.

Two important resources on discrete mathematics for teachers at all levels are the 1991 NCTM Yearbook Discrete Mathematics Across the Curriculum K-12 and the 1997 DIMACS Volume Discrete Mathematics in the Schools: Making an Impact. Teachers of grades 7-8 would also find useful the textbook Discrete Mathematics Through Applications.

The cumulative progresses indicators for grade 8 appear below in boldface type. Each indicator is followed by activities which illustrate how it can be addressed in the classroom in grades 7 and 8.

Building upon knowledge and skills gained in the preceding grades, experiences will be such that all students in grades 7-8:

6. Use systematic listing, counting, and reasoning in a variety of different contexts.

• Students determine the number of possible different sandwiches or hamburgers that can be created at local eateries using a combination of specified ingredients. They find the number of pizzas that can be made with three out of eight available toppings and relate the result to the numbers in Pascal's triangle.

• Students determine the number of dominoes in a set that goes up to 6:6 or 9:9, the number of candles used throughout Hannukah, and the number of gifts given in the song "The Twelve Days of Christmas," and connect the results through discussion of the triangular numbers. (Note that in a 6:6 set of dominoes there is exactly one domino with each combination of dots from 0 to 6.)

• Students determine the number of ways of spelling "Pascal" in the array below by following a path from top to bottom in which each letter is directly below, and just to the right or left of the previous letter.

  					P
  				A		A
  			S		S		S
  		C		C		C		C
  	A		A		A		A		A
  L		L		L		L		L		L

• Students design different license plate systems for different population sizes; for example, how large would the population be before you would run out of plates which had only three numbers, or only five numbers, or two letters followed by three numbers?

• Students find the number of different ways of making a row of six red and yellow flowers, organize and tabulate the possibilities according to the number of flowers of the first color, and explain the connection with the numbers in the sixth row of Pascal's triangle. (See also Visual Patterns in Pascal's Triangle.)

• Students pose and act out problems involving the number of different ways a group of people can sit around a table, using as motivation the scene of the Mad Hatter at the tea party. (See Mathematics, a Human Endeavor, p. 394.)

• Students count the total number of different cubes that can be made using either red or green paper for each face. (To solve this problem, they will have to use a "break up the problem into cases" strategy.)

• Students determine the number of handshakes that take place if each person in a room shakes hands with every other person exactly once, and relate this total to the number of line segments joining the vertices in a polygon, to the number of two-flavor ice-cream cones, and to triangular numbers.

• Students count the number of triangles or rectangles in a geometric design. For example, they should be able to count systematically the number of triangles (and trapezoids) in the figure below to the left, noting that there are triangles of three sizes, and the number of rectangles in the 4x5 grid pictured below to the right, listing first all dimensions of rectangles that are present.
  

7. Recognize common discrete mathematical models, explore their properties, and design them for specific situations.

• Students find the minimum number of colors needed to assign colors to all vertices in a graph so that any two adjacent vertices are assigned different colors and justify their answers. For example, students can explain why one of the graphs below requires four colors while for the other, three colors are sufficient.
  

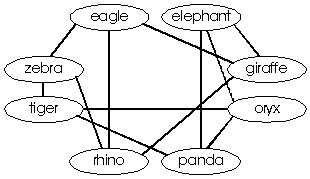• Students use graph coloring to solve problems which involve avoiding conflicts such as: scheduling the school's extra curricular activities; scheduling referees for soccer games; determining the minimum number of aquariums needed for a specified collection of tropical fish; and assigning channels to radio stations to avoid interference. In the graph at the right an edge between two animals indicates that they cannot share a habitat. The videotape, Geometry: New Tools for New Technologies has a segment Connecting the Dots: Vertex Coloring which discusses the minimum number of habitats required for this situation.

• Students use tree diagrams to represent and analyze possible outcomes in counting problems, such as tossing two dice.

• Students determine whether or not a given group of dominoes can be arranged in a line (or in a rectangle) so that the number of dots on the ends of adjacent dominoes match. For example, the dominoes (03), (05), (12), (14), (15), (23), (34) can be arranged as (12), (23), (30), (05), (51), (14), (43); and if an eighth domino (13) is added, they can be formed into a rectangle. What if instead the eighth domino was (24) - could they then be arranged in a rectangle or in a line?

• Students determine the minimum number of blocks that a police car has to repeat if it must try to patrol each street exactly once on a given map. Drawing Pictures With One Line contains similar real-world problems and a number of related game activities.

• Students find the best route for collecting recyclable paper from all classrooms in the school, and discuss different ways of deciding what is the "best." (See Drawing Pictures With One Line.)

• Students make models of various polyhedra with straws and string, and explore the relationship between the number of edges, faces, and vertices.

8. Experiment with iterative and recursive processes, with the aid of calculators and computers.

• Students develop a method for solving the Tower of Hanoi problem: There are three pegs, on the first of which five disks are stacked, each smaller than the ones underneath it (see diagram below); the problem is to move the entire stack to the third peg, moving disks, one at a time, from any peg to either of the other two pegs, with no disk ever placed upon a smaller one. How many moves are required to do this? What if there were 6 disks? How long would it take to do this with 64 disks? (An ancient legend predicts that when this task is completed, the world will end; should we worry?)
  

  Students view recursively Tower of Hanoi puzzles with various numbers of disks so that they can express the number of moves needed to solve the puzzle with one more disk in terms of the number of moves needed for the puzzle with the current number of disks.

• Students attempt to list the different ways they could travel 10 feet in a straight line if they were a robot which moved only in one or two foot segments, and then thinking recursively determine the number of different ways this robot could travel n feet.

• Students develop arithmetic and geometric progressions on a calculator.

• Students find square roots using the following iterative procedure on a calculator. Make an estimate of the square root of a number B, divide the estimate into B, and average the result with the estimate to get a new estimate. Then repeat this procedure until anadequate estimate is obtained. For example, if the first estimate of the square root of 10 is 3, then the second would be the average of 3 and 10/3, or 19/6 = 3.1666... . What is the next estimate of the square root of 10? How many repetitions are required to get the estimate to agree with the square root of 10 provided by the calculator?

• Students develop the sequence of areas and perimeters of iterations of the constructions of the Sierpinski triangle (top figures) and the Koch snowflake (bottom figures), and discuss the outcome if the process were continued indefinitely. (These are discussed in more detail in the sections for earlier grade levels. See Unit 1 of Fractals for the Classroom for related activities.)
  

  

• Students recognize the computation of the number of permutations as a recursive process - that is, that the number of ways of arranging 10 students is 10 times the number of ways of arranging 9 students.

9. Explore methods for storing, processing, and communicating information.

• Students conjecture which of the following (and other) methods is the most efficient way of handing back corrected homework papers which are already sorted alphabetically: (1) the teacher walks around the room handing to each student individually; (2) students pass the papers around, each taking their own; (3) students line themselves up in alphabetical order. Students test their conjectures and discuss the results.

• Students investigate and report about various codes that are commonly used, such as zip codes, UPCs (universal product codes) on grocery items, and ISBN numbers on books. (A good source for information about these and other codes is Codes Galore by J. Malkevitch, G. Froelich, and D. Froelich.)

• Students write a Logo procedure for making a rectangle that uses variables, so that they can use their rectangle procedure to create a graphic scene which contains objects, such as buildings, of varying sizes.

• Students are challenged to guess a secret word chosen by the teacher from the dictionary, using at most 20 yes-no questions. Is this always, or only sometimes possible?

• Students use Venn diagrams to solve problems like the following one from the New Jersey Department of Education's Mathematics Instruction Guide (p. 7-13). Suppose the school decided to add the springtime sport of lacrosse to its soccer and basketball offerings for its 120 students. A follow-up survey showed that: 35 played lacrosse, 70 played soccer, 40 played basketball, 20 played both soccer and basketball, 15 played both soccer and lacrosse, 15 played both basketball and lacrosse, and 10 played all three sports. Using this data, complete a Venn diagram and answer the following questions: How many students played none of the three sports? What percent of the students played lacrosse as their only sport? How many students played both basketball and lacrosse, but not soccer?

• Students keep a scrapbook of different ways in which information is stored or processed. For example a list of events is usually stored by date, so the scrapbook might contain a picture of a pocket calendar; a queue of people at a bank is usually processed in first-in-first-out (FIFO) order, so the scrapbook could contain a picture of such a queue. (How is this different from the waiting lines in a supermarket, or at a restaurant?)

• Students determine whether it is possible to have a year in which there is no Friday the 13th, and the maximum number of Friday the 13th's that can occur in one calendar year.

• Students predict and then explore the frequency of letters in the alphabet through examination of sample texts, computer searches, and published materials.

• Students decode messages where letters are systematically replaced by other letters without knowing the system by which letters are replaced; newspapers and games magazines are good sources for "cryptograms" and students can create their own. They also explore the history of code-making and code-breaking. The videotape Discrete Mathematics: Cracking the Code provides a good introduction to the uses of cryptography and the mathematics behind it.

10.Devise, describe, and test algorithms for solving optimization and search problems.

• Students find the shortest route from one city to another on a New Jersey map, and discuss whether that is the best route. (See Problem Solving Using Graphs.)

• Students write and solve problems involving distances, times, and costs associated with going from towns on a map to other towns, so that different routes are "best" according to different criteria.

• Students use binary representations of numbers to find winning strategy for Nim. (See Mathematical Investigations for other mathematical games.)

• Students plan an optimal route for a class trip. (See the Short-circuiting Trenton lesson in the Introduction to this Framework.)

• Students devise work schedules for employees of a fast-food restaurant which meet specified conditions yet minimize the cost.

• Students compare strategies for alphabetizing a list of words, and test to see which strategies are more efficient.

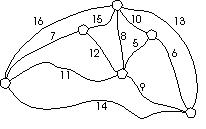• Students find a network of roads which connects a number of sites and involves the smallest cost. In the example at the right, what roads should be built so as to minimize the total cost, where the number on each road reflects the cost of building that road (in hundreds of thousands of dollars)?

• Students develop a precise description of the standard algorithm for adding two two-digit integers.

• Students devise strategies for dividing up the work of adding a long list of numbers among the members of the team.

References

Chavey, D. Drawing Pictures with One Line. Consortium for Mathematics and Its Applications (COMAP), Module #21, 1987.

Cozzens, M., and R. Porter. Problem Solving Using Graphs. Consortium for Mathematics and Its Applications (COMAP), Module #6, 1987.

Crisler, N., P. Fisher, and G. Froelich, Discrete Mathematics Through Applications. W. H. Freeman and Company, 1994.

Jacobs, H. R. Mathematics: A Human Endeavor. W. H. Freeman and Company, 1982.

Kenney, M. J., Ed. Discrete Mathematics Across the Curriculum K-12, 1991 Yearbook of the National Council of Teachers of Mathematics (NCTM). Reston, VA: 1991.

Malkevitch, J., G. Froelich, and D. Froelich, Codes Galore, Consortium for Mathematics and Its Applications (COMAP), Module #18, 1991.

New Jersey Department of Education. Mathematics Instruction Guide. D. Varygiannis, Coord. January 1996.

Peitgen, Heinz-Otto, et al. Fractals for the Classroom: Strategic Activities Volume One & Two. Reston, VA: NCTM and New York: Springer- Verlag, 1992.

Rosenstein, J. G., D. Franzblau, and F. Roberts, Eds. Discrete Mathematics in the Schools: Making an Impact. Proceedings of a 1992 DIMACS Conference on "Discrete Mathematics in the Schools." DIMACS Series on Discrete Mathematics and Theoretical Computer Science. Providence, RI: American Mathematical Society (AMS), 1997. (Available online from this chapter in http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/.)

Seymour, D. Visual Patterns in Pascal's Triangle. Palo Alto, CA: Dale Seymour Publications, 1986.

Souviney, R., et al. Mathematical Investigations. Book One, Dale Seymour Publications, 1990.

Video

Discrete Mathematics: Cracking the Code, Consortium for Mathematics and Its Applications.

Geometry: New Tools for New Technologies, videotape by the Consortium for Mathematics and Its Applications (COMAP). Lexington, MA, 1992.

On-Line Resources

http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/

The Framework will be available at this site during Spring 1997. In time, we hope to post additional resources relating to this standard, such as grade-specific activities submitted by New Jersey teachers, and to provide a forum to discuss the Mathematics Standards.