STANDARD 14 - DISCRETE MATHEMATICS
|
All students will apply the concepts and methods of discrete
mathematics to model and explore a variety of practical
situations.
|
Standard 14 - Discrete Mathematics - Grades 9-12
Overview
The five major themes of discrete mathematics, as discussed in the
K-12 Overview, are systematic listing, counting, and
reasoning; discrete mathematical modeling using graphs (networks) and
trees; iterative (that is, repetitive) patterns and processes;
organizing and processing information; and following and
devising lists of instructions, called
"algorithms," and using them to find the best
solution to real-world problems.
The following discussion of activities at the 9-12 grade levels
in discrete mathematics presupposes that corresponding
activities have taken place at the K-8 grade levels. Hence high
school teachers should review the discussions of discrete
mathematics at earlier grade levels and might use activities similar
to those described there before introducing the activities for
these grade levels.
At the high school level, students are becoming familiar with
algebraic and functional notation, and their understanding of all of
the themes of discrete mathematics and their ability to generalize
earlier activities should be enhanced by their algebraic skills and
understandings. Thus, for example, they should use formulas to
express the results of problems involving permutations and
combinations, relate Pascal's triangle to the coefficients of the
binomial expansion of (x+y)n, explore models
of growth using various algebraic models, explore iterations of
functions, and discuss methods for dividing an estate among several
heirs.
At the high school level, students are particularly interested in
applications; they ask What is all of this good for?
In all five areas of discrete mathematics, students should focus on
how discrete mathematics is used to solve practical
problems. Thus, for example, they should be able to apply their
understanding of counting techniques, to analyze lotteries; of graph
coloring, to schedule traffic lights at a local intersection; of paths
in graphs, to devise patrol routes for police cars; of iterative
processes, to analyze and predict fish populations in a pond or
concentration of medicine in the bloodstream; of codes, to understand
how bar-code scanners detect errors and how CD's correct errors;
and of optimization, to understand the 200 year old debates about
apportionment and to find efficient ways of scheduling the components
of a complex project.
Two important resources on discrete mathematics for teachers at all
grade levels are the 1991 NCTM Yearbook, Discrete Mathematics
Across the Curriculum K-12 and the DIMACS Volume, Discrete
Mathematics in the Schools: Making an Impact edited
by J. Rosenstein, D. Franzblau, and F. Roberts. Useful resources at
the high school level are Discrete Mathematics Through
Applications by N. Crisler, P. Fisher, and G. Froelich; For All
Practical Purposes: Introduction to Contemporary
Mathematics, by the Consortium for Mathematics and its
Applications; and Excursions in Modern Mathematics by
P. Tannenbaum and R. Arnold.
Standard 14 - Discrete Mathematics - Grades 9-12
Indicators and Activities
The cumulative progress indicators for grade 12 appear below in
boldface type. Each indicator is followed by activities which
illustrate how it can be addressed in the classroom in grades 9, 10,
11, and 12.
Building upon knowledge and skills gained in the preceding grades,
experiences will be such that all students in grades 9-12:
11. Understand the basic principles of iteration,
recursion, and mathematical induction.
- Students relate the possible outcomes of tossing five coins
with the binomial expansion of (x+y)5 and the fifth row of
Pascal's triangle, and generalize to values of n other
than 5.
- Students develop formulas for counting paths on grids or
other simple street maps.
- Students find the number of cuts needed in order to divide
a giant pizza so that each student in the school gets at least one
piece.
- Students develop a precise description, using
iteration, of the standard algorithm for adding two
integers.
12. Use basic principles to solve combinatorial and
algorithmic problems.
- Students determine the
number of ways of spelling "mathematics" in the array below
by following a path from top to bottom in which each letter is
directly below, and just to the right or left of the previous
letter.
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
A |
|
A |
|
|
|
|
|
|
|
T |
|
T |
|
T |
|
|
|
|
|
H |
|
H |
|
H |
|
H |
|
|
|
E |
|
E |
|
E |
|
E |
|
E |
|
| M |
|
M |
|
M |
|
M |
|
M |
|
M |
|
A |
|
A |
|
A |
|
A |
|
A |
|
|
|
T |
|
T |
|
T |
|
T |
|
|
|
|
|
I |
|
I |
|
I |
|
|
|
|
|
|
|
C |
|
C |
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
- Students determine the number of ways a committee of three
members could be selected from the class, and the number of ways three
people with specified roles could be selected. They generalize this
activity to finding a formula for the number of ways an n
person committee can be selected from a class of m people, and
the number of ways n people with specified roles can be
selected from a class of m people.
- Students find the number of ways of lining up thirty
students in a class, and compare that to other large numbers; for
example, they might compare it to the number of raindrops (volume = .1
cc) it would take to fill a sphere the size of the earth (radius =
6507 KM).
- Students determine the number of ways of dividing 52 cards
among four players, as in the game of bridge, and compare the number
of ways of obtaining a flush (five cards of the same suit) and a full
house (three cards of one denomination and two cards of another) in
the game of poker.
- Students play Nim (and similar games) and discuss winning
strategies using binary representations of numbers.
13. Use discrete models to represent and solve
problems.
- Students study the four color theorem and its
history. (The Mathematicians' Coloring Book
provides a good background for coloring problems.)
- Students using graph coloring to determine the minimum
number of guards (or cameras) needed for museums of various shapes
(and similarly for placement of lawn sprinklers or motionsensor
burglar alarms).
- Students use directed graphs to represent tournaments
(where an arrow drawn from A to B represents "A defeats B")
and food webs (where an arrow drawn from A to B represents "A
eats B"), and to construct oneway orientations of streets in a
given town which involve the least inconvenience to drivers. (A
directed graph is simply a graph where each edge is thought of as an
arrow pointing from one endpoint to the other.)
- Students use tree diagrams to analyze the play of games
such as tic-tac-toe or Nim, and to represent the solutions to weighing
problems. Example: Given 12 coins one of which is "bad,"
find the bad one, and determine whether it is heavier or lighter than
the others, using three weighings.
- Students use graph coloring to schedule the school's
final examinations so that no student has a conflict, if at all
possible, or to schedule traffic lights at an intersection.
- Students devise graphs for which there is a path that
covers each edge of the graph exactly once, and other graphs which
have no such paths, based on an understanding of necessary and
sufficient conditions for the existence of such paths, called
"Euler paths," in a graph. Drawing Pictures With One
Line provides background and applications for Euler path
problems.
- Students make models of polyhedra with straws and string,
and explore the relationship between the numbers of edges, faces, and
vertices, and generalize the conclusion to planar graphs.
- Students use graphs to solve problems like the
"fire-station problem": Given a city where the
streets are laid out in a grid composed of many square blocks, how
many fire stations are needed to provide adequate coverage of
the city if each fire station services its square block and the
four square blocks adjacent to that one? The Maryland Science
Center in Baltimore has a hands-on exhibit involving a fire-station
problem for 35 square blocks arranged in a six-by-six grid with one
corner designated a park.
14. Analyze iterative processes with the aid of
calculators and computers.
- Students analyze the Fibonacci sequence 1, 1, 2, 3, 5, 8,
13, 21, ... as a recurrence relation A
n + 2 = An +
An + 1 with connections to the golden
ratio. Fascinating Fibonaccis illustrates a variety of
connections between Fibonacci numbers and the golden ratio.
- Students solve problems involving compound
interest using iteration on a calculator or on a
spreadsheet.
- Students explore examples of linear growth, using
the recursive model based on the formula An+1 =
An + d, where d is the common difference, and convert it
to the explicit linear formula, An+1 = A1 + n
× d.
- Students explore examples of population growth,
using the recursive model based on the formula An+1 =
An x r, where r is the common multiple or growth rate,
convert it to the explicit exponential formula An+1 =
A1 rn, and apply it to both economics (such as
interest problems) and biology (such as concentration of medicine in
blood supply).
- Students explore logistic growth models of
population growth, using the recursive model based on the formula
An+1 = An x (1 - An) x r, where
r is the growth rate and An is the fraction of the
carrying capacity of the environment, and apply this to the population
of fish in a pond. Using a spreadsheet, students experiment with
various values of the initial value A1 and of the growth
rate, and describe the relationship between the values chosen and the
long term behavior of the population.
- Students explore the pattern resulting from
repeatedly multiplying
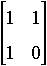 by itself.
by itself.
- Students use a calculator or a computer to study
simple Markov chains, such as weather prediction and population growth
models. (See Chapter 7.3 of Discrete Mathematics Through
Applications.)
- Students explore graphical iteration by choosing
a function key on a calculator and pressing it repeatedly, after
choosing an initial number, to get sequences of numbers like 2, 4, 8,
16, 32, ... or 2, sqrt(2), sqrt(sqrt(2)),
sqrt(sqrt(sqrt(2))),
.... . They use the graphs of the functions to explain the behavior of
the sequences obtained. They extend these explorations by iterating
functions they program into the calculator, such as linear functions,
where slope is the predictor of behavior, and quadratic functions f
(x) = ax (1 - x), where 0< x <1 and 1< a <4, which
exhibit chaotic behavior.
- Students explore iteration behavior using the function
defined by the two cases
-
| f(x) = x + 1/2 |
for x between 0 and 1/2 |
| f(x) = 2 - 2x |
for x between 1/2 and 1 |
They use the initial values 1/2, 2/3, 5/9, and 7/10, and then, with
a calculator or computer, the initial values .501, .667, and .701
(which differ by a small amount from the first group of
"nice" initial values). They compare the behavior of the
sequences generated by these values to the sequences generated by the
previous initial values.
- Students play the Chaos Game. Each pair
of students is provided with an identical transparency on which have
been drawn the three vertices L, T, and R of an equilateraltriangle.
Each team starts by selecting any point on the triangle. They roll a
die and create a new point halfway to L if they roll 1 or 2, halfway
to R if they roll 3 or 4, and halfway to T if they roll 5 or 6. They
repeat 20 times, each time using the new point as the starting point
for the next iteration. The teacher overlays all of the
transparencies and out of this chaos comes ... the familiar Sierpinski
triangle. (The Sierpinski triangle is discussed in detail in the
sections for earlier grade levels. Also see Unit 2 in Fractals for
the Classroom. The Chaos Game software allows
students to try variations and explore the game
further.)
15. Apply discrete methods to storing, processing, and
communicating information.
- Students discuss various algorithms used for sorting large
numbers of items alphabetically or numerically, and explain why some
sorting algorithms are substantially faster than others. To introduce
the topic of sorting, give each group of students 100 index cards each
with one word on it, and let them devise strategies for efficiently
putting the cards into alphabetical order.
- Students discuss how scanners of bar codes (zip
codes, UPCs, and ISBNs) are able to detect errors in reading the
codes, and evaluate and compare how error-detection is accomplished in
different codes. (See the COMAP Module Codes Galore or Chapter
9 of For All Practical Purposes.)
- Students investigate methods of error correction
used to transmit digitized pictures from space (Voyager or Mariner
probes, or the Hubble space telescope) over noisy or unreliable
channels, or to ensure the fidelity of a scratched CD recording. (See
Chapter 10 of For All Practical Purposes.)
- Students read about coding and code-breaking machines and
their role in World War II.
- Students research topics that are currently discussed in
the press, such as public-key encryption, enabling messages to be
transmitted securely, and data-compression, used to save space on a
computer disk.
16. Apply discrete methods to problems of voting,
apportionment, and allocations, and use fundamental strategies
of optimization to solve problems.
- Students find the best route when a number of alternate
routes are possible. For example: In which order should you pick
up the six friends you are driving to the school dance? In
which order should you make the eight deliveries for the drug
store where you work? In which order should you visit the
seven "must-see" sites on your vacation
trip? In each case, you want to find the "best route,"
the one which involves the least total distance, or least total time,
or least total expense. Students create their own problems, using
actual locations and distances, and find the best route. For a larger
project, students can try to improve the route taken by their school
bus.
- Students study the role of apportionment in American
history, focusing on the 1790 census (acting out the positions of the
thirteen original states and discussing George Washington's first
use of the presidential veto), and the disputed election of 1876, and
discuss the relative merits of different systems of apportionment that
have been proposed and used. (This activity provides an opportunity
for mathematics and history teachers to work together.) They also
devise a student government where the seats are fairly
apportionedamong all constituencies. (See the COMAP module The
Apportionment Problem or Chapter 14 of For All Practical
Purposes.)
- Students analyze mathematical methods for dividing an
estate fairly among various heirs. (See Chapter 2 of Discrete
Mathematics Through Applications, Chapter 3 of Excursions in
Modern Mathematics, or Chapter 13 of For All Practical
Purposes.)
- Students discuss various methods, such as preference
schedules or approval voting, that can be used for determining the
winner of an election involving three or more candidates (for example,
the prom king or queen). With preference schedules, each voter ranks
the candidates and the individual rankings are combined, using various
techniques, to obtain a group ranking; preference schedules are used,
for example, in ranking sports teams or determining entertainment
awards. In approval voting, each voter can vote once for each
candidate which she finds acceptable; the candidate who receives the
most votes then wins the election. (See the COMAP module The
Mathematical Theory of Elections or Chapter 11 of For All
Practical Purposes.)
- Students find an efficient way of doing a complex project
(like preparing an airplane for its next trip) given which tasks
precede which and how much time each task will take. (See Chapter 8 of
Excursions of Modern Mathematics or Chapter 3 of For All
Practical Purposes.)
- Students find an efficient way of assigning songs of
various lengths to the two sides of an audio tape so that the total
times on the two sides are as close together as possible. Similarly,
they determine the minimal number of sheets of plywood needed to build
a cabinet with pieces of specified dimensions.
- Students apply algorithms for matching in graphs to
schedule when contestants play each other in the different rounds of a
tournament.
- Students devise a strategy for finding a "secret
number" from 1 to 1000 using questions of the form Is your
number bigger than 837? and determine the least number of
questions needed to find the secret number.
References
-
Bennett, S., D. DeTemple, M. Dirks, B. Newell, J. Robertson, and
B. Tyus. The Apportionment Problem:
The Search for the Perfect Democracy. Consortium for Mathematics
and Its Applications (COMAP), Module #18, 1986.
Chavey, D. Drawing Pictures with One Line. Consortium
for Mathematics and Its Applications (COMAP), Module #21, 1987.
Consortium for Mathematics and Its Applications. For All
Practical Purposes: Introduction to
Contemporary Mathematics. W. H. Freeman and Company,Third
Edition, 1993.
Crisler, N., P. Fisher, and G. Froelich, Discrete Mathematics
Through Applications. W. H. Freeman and Company, 1994.
Francis, R. The Mathematician's Coloring
Book. Consortium for Mathematics and Its Applications
(COMAP), Module #13, 1989.
Garland, T. H. Fascinating Fibonaccis. Palo Alto, CA:
Dale Seymour Publications, 1987.
Kenney, M. J., Ed. Discrete Mathematics Across the Curriculum
K-12, 1991 Yearbook of the National Council of Teachers of
Mathematics (NCTM). Reston, VA, 1991.
Malkevitch, J. The Mathematical Theory of Elections.
Consortium for Mathematics and Its Applications (COMAP). Module
#1, 1985.
Malkevitch, J., G. Froelich, and D. Froelich. Codes
Galore. Consortium for Mathematics and Its Applications
(COMAP). Module #18, 1991.
Peitgen, Heinz-Otto, et al. Fractals for the Classroom:
Strategic Activities Volume One & Two. Reston, VA: NCTM and
New York: Springer-Verlag, 1992.
Rosenstein, J. G., D. Franzblau, and F. Roberts, Eds.
Discrete Mathematics in the Schools:
Making an Impact. Proceedings of a 1992 DIMACS Conference
on "Discrete Mathematics in the Schools." DIMACS Series
on Discrete Mathematics and Theoretical Computer Science.
Providence, RI: American Mathematical Society (AMS), 1997.
(Available online from this chapter in
http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/.)
Seymour, D. Patterns in Pascal's Triangle.
Poster. Palo Alto, CA: Dale Seymour Publications.
Tannenbaum, P. and R. Arnold. Excursions in Modern
Mathematics. Prentice-Hall, 1992.
Software
-
The Chaos Game. Minnesota Educational Computer Consortium
(MECC).
On-Line Resources
-
http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/
The Framework will be available at this site during
Spring 1997. In time, we hope to post additional resources
relating to this standard, such as grade-specific activities submitted
by New Jersey teachers, and to provide a forum to discuss the
Mathematics Standards.
|
 by itself.
by itself.