LEARNING ENVIRONMENT STANDARD 18
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| All students will be evaluated using a diversity of assessment tools and strategies to provide multiple indicators of the quality of every student's mathematical learning and of overall program effectiveness. |
(This "learning environment standard" was developed and approved by the task force that prepared the Mathematics Standards and appears in the Introduction to the Mathematics Standards chapter of the New Jersey State Department of Education's Core Curriculum Content Standards; however, since it was not considered a "content standard," it was not presented to the New Jersey Board of Education for adoption.)
Descriptive Statement
A variety of assessment instruments should be used to enable the teacher to monitor students' progress in understanding mathematical concepts and in developing mathematical skills. Assessment of mathematical learning should not be confined to intermittent standardized tests. The learning environment should embody the perspective that the primary function of assessment is to improve learning.
Overview
An important goal of this chapter is to broaden understanding of both the purposes and the tools of assessment. The popular conception of assessment is restricted to evaluating individual student performance by tests designed to determine, at the end of a unit of time or instruction, what the student has already learned. But assessment should also be used during the learning process to enable teachers to monitor students' understanding and to modify curriculum and instruction, as well as to assess the effectiveness of school programs. Assessment of individual student performance should be a continuous process that involves many types of assessment activity. Students should play active roles in assessment so that each assessment experience is also an educational experience.
This chapter therefore has three main sections, dealing with, Alternative Assessment Strategies, The Student's Role in Assessment, and Educational Purposes of Assessment.
The Assessment Standards for School Mathematics of the National Council of Teachers of Mathematics describes assessment as "the process of gathering evidence about a student's knowledge of, ability to use, and disposition toward mathematics, and of making inferences from that evidence for a variety of purposes." The kinds of inferences that can be drawn from that evidence are discussed in the section on Educational Purposes of Assessment.
However, it is important to establish at the outset the perspective that the major purpose of assessment is to promote learning. The assessment is not the goal, but a means to achieve a goal. Measuring What Counts, a 1993 Policy Brief of the Mathematical Science Education Board, begins as follows:
"You can't fatten a hog by weighing it." So said a farmer to a governor at a public hearing in order to explain in plain language the dilemma of educational assessment. To be useful to society, assessment must advance education, not merely record its status.
Measuring What Counts lists "three fundamental educational principles which form the foundation of all assessment that supports effective education":
- The Content Principle - Assessment should reflect the mathematics that is most important for students to learn.
- The Learning Principle - Assessment should enhance mathematics learning and support good instructional practice.
- The Equity Principle - Assessment should support every student's opportunity to learn important mathematics.
These three principles are reflected in the first three cumulative progress indicators for this standard.
Experiences will be such that all students:
1. Are engaged in assessment activities that function primarily to improve learning.
2. Are engaged in assessment activities based upon rich, challenging problems from mathematics and other disciplines.
3. Are engaged in assessments activities that address the content described in all New Jersey's Mathematics Standards.
The Content Principle, the Learning Principle, and the Equity Principle were incorporated into the first three of the six assessment standards in the NCTM Assessment Standards for School Mathematics:
- Assessment should reflect the mathematics that all
students need to know and be able to do.
-
New Jersey's Mathematics Standards provide a vision of the mathematics that all students should know and be able to do. Assessment should match this vision.
-
- Assessment should enhance mathematics learning.
-
Assessments should be learning opportunities as well as opportunities for students to demonstrate what they know and can do. Although assessment is done for a variety of reasons, its main goal is to improve students' learning and inform teachers as they make instructional decisions. As such, it should be a routine part of ongoing classroom activity rather than an interruption.
-
- Assessment should promote equity.
-
Assessment should be a means of fostering growth toward high expectations rather than a filter used to deny students the opportunity to learn important mathematics. In an equitable assessment, each student has an opportunity to demonstrate her or his mathematical power; this can only be accomplished by providing multiple approaches to assessment, adaptations for bilingual and special education students, and other adaptations for students with special needs. Assessment is equitable when students have access to the same accommodations and modifications that they receive in instruction.
-
- Assessment should be an open process.
-
Three aspects of assessment are involved here. First, information about the assessment process should be available to those affected by it, the students. Second, teachers should be active participants in all phases of the assessment process. Finally, the assessment process should be open to scrutiny and modification.
-
- Assessment should promote valid inferences about
mathematics learning.
-
A valid inference is based on evidence that is adequate and relevant. The amount and type of evidence that is needed depends upon the consequences of the inference. For example, a teacher may judge students' progress in understanding place value through informal interviews and use this information to plan future classroom activities. However, a large-scale, high-stakes assessment such as the HSPT11 requires much more evidence and a more formal analysis of that evidence.
-
- Assessment should be a coherent process.
-
Three types of coherence are involved in assessment. First, the phases of assessment must fit together. Second, the assessment must match the purpose for which it is being conducted. Finally, the assessment must be aligned with the curriculum and with instruction.
-
These principles should be kept in mind as changes in assessment strategies are contemplated, developed, tested, and implemented. They should be kept in mind by classroom teachers and all others involved in assessment - for example, district committees selecting a standardized norm-referenced test, district supervisors or department chairs analyzing data from a collection of student portfolios, and state mathematics content development committees reviewing proposed test items for the statewide tests.
Alternative Assessment Strategies
The next cumulative progress indicator for this standard refers to a wide variety of assessment techniques that are now available to help make informed judgments and to assure continued progress.
Activities will be such that all students:
4. Demonstrate competency through varied assessment methods including, but not limited to, individual and group tests, authentic performance tasks, portfolios, journals, interviews, seminars, and extended projects.
Making use of a variety of assessment methods provides a more complete picture of students' learning. Some types of assessment tasks provide information about students' abilities to perform mathematical procedures. Others involve higher-level thinking and problem-solving skills, represent meaningful instructional activities, and/or invoke real-world applications. Stenmark (1991) describes some of the changes in mathematics learning that result from using these alternative assessment strategies:
Students:
- think more deeply about problems;
- feel free to do their best thinking because their ideas are valued;
- ask deeper and more frequent questions of themselves, their classmates, and their teachers;
- improve their listening skills and gain an appreciation for the role of listening in cooperative work;
- feel responsibility for their thoughts and ownership of their methods;
- observe that there are many right ways to solve a problem;
- experience the value of verbalization as a means of clarifying one's thinking;
- form new insights into mathematical concepts;
- learn ways to identify the places they need help;
- increase their self-confidence and self-esteem as a result of genuine interest shown by a teacher or classmate;
- feel more tolerance and respect for other people's ideas;
- focus their energy on exploring and communicating ideas about mathematical relationships rather than simply finding answers;
- develop strategies for conducting self-interviews while solving problems in other settings;
- find satisfaction and confidence in their ability to solve problems; and
- look less to the teacher for clues about the correctness of their methods and focus less on imitating the "right" way.
Teachers:
- gain access to student thinking;
- enhance their ability to use nonthreatening questions that elicit explanations and reveal misconceptions;
- strengthen their listening skills;
- show respect for students by being nonjudgmental;
- use interview results as a source of questions to pose on written assignments for the whole class;
- encourage respect for diversity by modeling appreciation of varied approaches;
- pose questions that encourage students to construct and share their own understandings;
- feel reinforcement for letting go of "teaching as telling."
A good source of samples of different types of assessment tasks is Mathematics Assessment: Myths, Models, Good Questions, and Practical Suggestions (Stenmark, 1991). Many of the examples and definitions in this section come from that source.
Individual and Group Tests
Traditionally, the dominant mode of assessment has been paper-and-pencil testing of individual students. This testing often includes both selected-response items - such as matching, multiple-choice, and true/false questions - and constructed-response items - such as problems to solve, or short-answer, fill in the blank, or "show your work" questions. Large-scale testing often uses primarily selected-response items, since these are easy to score. However, constructing good selected-response test items is quite difficult, so many teachers rely more on constructed-response items for classroom assessments. Some teachers check only answers, while others ask students to show their work and provide partial credit to varying degrees. More recently, individual tests have also begun to include open-ended questions ("solve and explain your solution"), such as those found on New Jersey's Eighth-Grade Early Warning Test (EWT) and Eleventh-Grade High School Proficiency Test (HSPT), since these provide more insight intostudent thinking. The following are some suggestions for creating and/or selecting open-ended questions, as well as for lightening the burden created by having students write.
 |
SUGGESTIONS |
 The questions should be constructed so that they cannot be
answered by simple multiple-choice responses. They should address the
ability of the student to form and communicate mathematical ideas and
arguments, see and make connections between the various content
strands of mathematics, make conjectures, justify results, organize
and analyze data, and make estimates and predictions based on
incomplete data or patterns of events.
The questions should be constructed so that they cannot be
answered by simple multiple-choice responses. They should address the
ability of the student to form and communicate mathematical ideas and
arguments, see and make connections between the various content
strands of mathematics, make conjectures, justify results, organize
and analyze data, and make estimates and predictions based on
incomplete data or patterns of events.
 When students have been using an arithmetic operation or
algebraic procedure, ask them to explain, in writing, or with a
diagram, what that operation or procedure means and how it works.
When students have been using an arithmetic operation or
algebraic procedure, ask them to explain, in writing, or with a
diagram, what that operation or procedure means and how it works.
 The New Jersey Department of Education's Mathematics
Instructional Guide: Linking Classroom Experiences to Current
Statewide Assessments provides many examples of open-ended
questions for the 7-12 grade levels. Problems used in other
states' assessment programs can be found in the National Council
of Supervisors of Mathematics' Great Tasks and More!!, A
Source Book of Camera-Ready Resources on Mathematics
Assessment.
The New Jersey Department of Education's Mathematics
Instructional Guide: Linking Classroom Experiences to Current
Statewide Assessments provides many examples of open-ended
questions for the 7-12 grade levels. Problems used in other
states' assessment programs can be found in the National Council
of Supervisors of Mathematics' Great Tasks and More!!, A
Source Book of Camera-Ready Resources on Mathematics
Assessment.
 Ask students to explain how they got their answers. This works
quite well not only for textbook word problems but also for mental
math and estimation problems.
Ask students to explain how they got their answers. This works
quite well not only for textbook word problems but also for mental
math and estimation problems.
 Sample student papers randomly. Select a few papers or a few
questions on each paper each day to review. Be selective about what
is commented on; choose one or two aspects for evaluation or scoring
and detailed feedback.
Sample student papers randomly. Select a few papers or a few
questions on each paper each day to review. Be selective about what
is commented on; choose one or two aspects for evaluation or scoring
and detailed feedback.
 Teach students to assess each others' work. Review sample
student answers with the class, asking students to suggest
improvements. Share scoring rubrics with the students.
Teach students to assess each others' work. Review sample
student answers with the class, asking students to suggest
improvements. Share scoring rubrics with the students.
 Evaluation of open-ended questions can be done in several ways.
For classroom tasks, the "piles" method is often appropriate
and efficient; put each paper as it is read in one of three (or more)
piles so that comparable papers are in the same pile. Labels or
points can be assigned to the piles after all of the papers are
sorted. For assessments with more substantial consequences, it is
important to ensure the reliability of the scoring (two different
graders will give the same paper the same score); thus, scoring
rubrics have been developed. Some of these are quite general, such as
the one on the following page that is used in New Jersey's
statewide assessments; this scoring guide can be found in the New
Jersey State Department of Education's Grade 11 High School
Proficiency Test: Directory of Test Specification and
Items. Other scoring rubrics can be found in the National Council
of Supervisors of Mathematics' Great Tasks and More!!, A
Source Book of Camera-Ready Resources on Mathematics
Assessment.
Evaluation of open-ended questions can be done in several ways.
For classroom tasks, the "piles" method is often appropriate
and efficient; put each paper as it is read in one of three (or more)
piles so that comparable papers are in the same pile. Labels or
points can be assigned to the piles after all of the papers are
sorted. For assessments with more substantial consequences, it is
important to ensure the reliability of the scoring (two different
graders will give the same paper the same score); thus, scoring
rubrics have been developed. Some of these are quite general, such as
the one on the following page that is used in New Jersey's
statewide assessments; this scoring guide can be found in the New
Jersey State Department of Education's Grade 11 High School
Proficiency Test: Directory of Test Specification and
Items. Other scoring rubrics can be found in the National Council
of Supervisors of Mathematics' Great Tasks and More!!, A
Source Book of Camera-Ready Resources on Mathematics
Assessment.
|
The General Scoring Guide Student Demonstrates Proficiency - Score Point = 3 The student provides a satisfactory response with explanations which are plausible, reasonably clear, and reasonably correct, e.g., includes appropriate diagram(s), uses appropriate symbols or language to communicate effectively, exhibits an understanding of the "mathematics" of the problem, uses appropriate processes and/or descriptions to answer the question, and presents sensible supporting arguments. Any flaws in the response are minor. Student Demonstrates Minimal Proficiency - Score Point = 2 The student provides a "nearly satisfactory" response which contains some flaws, e.g., begins to answer the question correctly but fails to answer all of its parts or omits appropriate explanation, draws diagram(s) with minor flaws, makes some errors in computation, misuses mathematical language, or uses inappropriate strategies to answer the question under consideration. Student Demonstrates a Lack of Proficiency - Score Point = 1 The student provides a less than satisfactory response that only begins to answer the question, but fails to answer it completely, e.g., provides little or no appropriate explanation, draws diagram(s) which are unclear, exhibits little or no understanding of the question being asked, or makes major computational errors. Student Demonstrates No Proficiency - Score Point = 0 The student provides an unsatisfactory response that answers the question inappropriately, e.g., uses algorithms which do not reflect any understanding of the question, makes drawings which are inappropriate to the question, provides a copy of the question without an appropriate answer, fails to provide any information which is appropriate to the question, or fails to attempt to answer the question. (New Jersey State Department of Education) |
 Develop a specific scoring rubric for the item that you are
using. This initial analysis of your item will help you to consider
exactly what a "good" response should include. Remember,
however, that students may come up with an approach that you have not
previously considered, so be ready to adapt your rubric as necessary.
Sample scoring rubrics for individual problems can be found in the
publications cited above from the New Jersey State Department of
Education and the National Council of Supervisors of Mathematics.
Develop a specific scoring rubric for the item that you are
using. This initial analysis of your item will help you to consider
exactly what a "good" response should include. Remember,
however, that students may come up with an approach that you have not
previously considered, so be ready to adapt your rubric as necessary.
Sample scoring rubrics for individual problems can be found in the
publications cited above from the New Jersey State Department of
Education and the National Council of Supervisors of Mathematics.
 Use an analytic scoring rubric for problem-solving tasks that
rates students on three phases of problem-solving: understanding the
problem, developing a solution plan, and finding the answer. The
rubric in the following table assigns three scores for a problem, one
for each phase. Each of the three can vary from 0 to 2. The
advantage of this type of rubric is that it provides more specific
information about where students are having difficulty than does a
general scoring rubric.
Use an analytic scoring rubric for problem-solving tasks that
rates students on three phases of problem-solving: understanding the
problem, developing a solution plan, and finding the answer. The
rubric in the following table assigns three scores for a problem, one
for each phase. Each of the three can vary from 0 to 2. The
advantage of this type of rubric is that it provides more specific
information about where students are having difficulty than does a
general scoring rubric.
| Analytic Scoring Guide | |
| Understanding the Problem |
0: Complete misunderstanding of the problem 1: Part of the problem misunderstood or misinterpreted 2: Complete understanding of the problem |
| Planning the Solution |
0: No attempt, or totally inappropriate plan 1: Partially correct plan based on part of the problem being interpreted correctly 2: Plan could have led to a correct solution if implemented properly |
| Getting an Answer |
0: No answer, or wrong answer based on an inappropriate plan 1: Copying error; computational error; partial answer for a problem with multiple answers 2: Correct answer and correct label for the answer |
Open-ended questions and scoring rubrics can be used for group as well as individual tests. Such tests are particularly appropriate for assessing problem solving, reasoning, communication, and use of tools and technology. These tests may involve open-ended questions that must be answered with a single written response from the group (a paragraph, a letter, a graph, or a poster), or they may involve observing the group as it works for indications of appropriate understanding and use of the mathematical concepts and techniques. Some teachers like to combine both methods, observing students working together in a group and then having them write up independent responses based on their group work. Students may be assigned to groups randomly (e.g., by drawing a card) or they may be tested in the same groups in which they have been working.
Authentic Performance Tasks
An authentic performance assessment starts with asking a student or group of students to engage in some mathematical task or investigation. Observations of the students as they work, questioning of the processes they use to solve the task, and examination of their final results are all standard activities that create useful data about what the students know and are able to do. Great care must be taken to be sure that the task is rich and motivating enough to produce sustained effort on the part of the students. Tasks which are boring or too simple will not be very good performance assessment tasks.
|
How Many Buttons? Ms. Allen's fourth-graders had just finished a unit on numeration that emphasized estimation. As a review, she had them estimate the number of buttons in their class on that day, collect and analyze data, and share their results with the class. As a performance task, she had them work in pairs the next day to estimate the number of buttons in the school on that day. Ms. Allen has developed what she calls a protorubric - the beginning of a scoring rubric - which she will refine as she reviews the students' papers.
(Adapted from Measuring Up, 1993, pp. 95-100) |
The above task is adapted from Measuring Up: Prototypes for Mathematic Assessment which provides a number of assessment activities for the middle grades. The following sample performance tasks are adapted from Stenmark (1991, pp. 14-22):
- Ask a group of third graders who are learning about fractions to show you with manipulatives how they would divide different items, such as 5 candy bars, 10 pencils, or 11 comic books, among 4 students.
- Have students explain how they would teach a younger sibling to understand the meaning of tens and ones in place value.
- Give a group of high school students the task of finding the function that "best fits" certain data by using computer software and a printout of their results.
- Ask students, "How many bicycles are there within two miles of this school?" Have them make a plan for investigating the question and prepare an oral report, with overheads or other displays, for the class.
- Ask a group of seventh graders, "If you measured an object with five different rulers and got five different answers, how would you decide which answer was correct?"
|
Sample Performance Task- South Brunswick Teachers in South Brunswick have been working on a plan to use at least one common performance assessment task across all sections of each grade level in the district. Some of the tasks they've settled on for the first year of the program are:
|
Designing appropriate performance tasks is not a simple procedure. Many guidelines must be considered and the tasks must be tested with real students before they can be used on a wide scale. A useful set of criteria for the tasks is presented in the following table, attributed in NCTM's Mathematics Assessment to Leinwand and Wiggins:
| Criteria For Performance Tasks | ||
| A good task is: | rather than: | meaning that: |
| Essential | Tangential |
- The task fits into the core of the curriculum. - It represents a "big idea." |
| Authentic | Contrived |
- It uses processes appropriate to the discipline. - Students value the outcome of the task. |
| Rich | Superficial |
- The task leads to other problems. - It raises other questions. - It has many possibilities. |
| Engaging | Uninteresting |
- The task is thought-provoking. - It fosters persistence. |
| Active | Passive |
- The student is the worker and decision-maker. - Students interact with other students. - They construct meaning and deepen understanding. |
| Feasible | Infeasible |
- The task can be done within the allotted time. - It is developmentally appropriate for students. |
| Equitable | Inequitable |
- The task develops thinking in a variety of styles. |
| Open | Closed |
- It contributes to positive attitudes. - The task has more than one right answer. - It has multiple avenues of approach, making it accessible to all students. |
Portfolios
A portfolio is a showcase of student work; it is a place where students can demonstrate their mathematical power in specific and general ways. Student thinking, growth over time, mathematical connections, students' views of themselves as mathematicians, and the problem-solving process are each emphasized in creating, maintaining, revising, and assessing student portfolios. In addition, teachers should be working with students to regularly review their portfolios in order to establish short-term and long-term goals.
What's in a portfolio? Many of the following kinds of items may be included in portfolios. Of course, no one student would be asked to present all of these:
|
- table of contents - introductory and self-assessment letters - long-term projects - daily notes - journal entries - excerpts from dialogue notebooks - test problems - physical models of mathematical concepts - mathematical models of real world phenomena - interviews between student and peer - interviews between student and teacher - art work done by the student - a mathematical autobiography |
- audio and video tapes of work in progress and/or finished products - scale drawings - photographs - homework - peer critiques and evaluations - commentary from parents about portfolio contents - self-generated problems and solutions - papers showing student's corrections of errors and misconceptions - teacher observations of student - group projects - excerpts from team notebooks |
Students can be informed about their specific portfolio assignment through discussion of the following sample hand-out:
|
|||||||||||||||||||||||||||
Evaluation of portfolios may be accomplished in much the same way as performance tasks or open-ended tasks. Vermont uses a portfolio rating system for grades 4 and 8 in which seven pieces of work are rated on a four-point scale for understanding of the task, quality of approaches/procedures, decisions along the way, outcomes of activities, use of mathematical language, use of mathematical representations (graphs, tables, diagrams, manipulatives, etc.), and clarity of presentation. Portfolios are also used to provide a picture of the instructional opportunities, the content areas of programs, and anecdotal indicators of disposition towards mathematics. Most classroom teachers do not use such an elaborate rubric, preferring to use a more holistic approach, such as the following:
-
Level 4 (top level) Exciting! Includes a variety of work, with evidence of use of many different resources. Papers show understanding of content, organization and analysis of information, clarity of communication, enthusiasm for math. Includes self-assessment. Level 3 Variety of work. Fairly good explanations, with some use of resources. Good understanding of basic mathematics processes. Missing indications of enthusiasm, self-assessment, extensive investigations, and/or student analysis of information. Level 2 Little evidence of original thinking. Minimal student explanations. Over-concentration on low-level tasks, such as computation. Level 1 Almost no creative work. Mostly ditto sheets or textbook problems. Almost no evidence of student thinking. No evidence of discussion of mathematical ideas. No explanations. (Adapted from Stenmark, 1991, p. 44)
Managing the development and review of portfolios is a time-consuming process. Following are some suggestions to help streamline that process.
 |
SUGGESTIONS |
 To demonstrate students' growth over time, pose similar
questions periodically throughout the year. These questions should
explore the same content in different situations.
To demonstrate students' growth over time, pose similar
questions periodically throughout the year. These questions should
explore the same content in different situations.
 Include observation checklists, interview notes, and parent
communications regularly.
Include observation checklists, interview notes, and parent
communications regularly.
 Keep two portfolios for each student, a work portfolio and an
assessment portfolio. Have younger students keep work portfolios in a
plastic crate or box to pick up as they enter the room; older students
may use a notebook. Include journals in portfolios and put copies of
group work in the folders of each group member. Every two to six
weeks, have students review their work portfolios. They should make a
list of all the work they have completed, make revisions if they wish,
review their journals, and circle or label pieces that they feel
reflect growth or understanding. Ask them to select work to put in
their assessment portfolio, writing a paragraph about each item
selected.
Keep two portfolios for each student, a work portfolio and an
assessment portfolio. Have younger students keep work portfolios in a
plastic crate or box to pick up as they enter the room; older students
may use a notebook. Include journals in portfolios and put copies of
group work in the folders of each group member. Every two to six
weeks, have students review their work portfolios. They should make a
list of all the work they have completed, make revisions if they wish,
review their journals, and circle or label pieces that they feel
reflect growth or understanding. Ask them to select work to put in
their assessment portfolio, writing a paragraph about each item
selected.
Journals
Another assessment strategy being used by New Jersey teachers is the Math Journal, a small booklet or notebook section in which students write on a regular basis. A journal entry can be a regular daily part of the math class or something just done occasionally. It can be very structured, with the students responding to a writing prompt from the teacher, or very free, with the students choosing their own math topic and question to write about. The journal is not graded, since teachers want students to write freely in it. The consistent aspect of the journal is that it provides a means of communication between the student and the teacher. It is a vehicle by which the student can express understanding, attitudes, delight, creativity, and a myriad of other responses. Students frequently have a hard time creating journal entries when they first begin to write them, especially if they are already well-advanced in school. Some sample prompts, from a collection being created in South Brunswick, are shown below. They can help children feel more comfortable and more focused in constructing an entry.
|
Sample Journal Prompts
|
Teachers who have students write in their journals are, of course, obligated to read and respond frequently to the entries. But they will find many of the students' responses refreshing and original and the process will be one of the most pleasant of their tasks. To reduce the amount of time spent reading journals, some teachers have students box or underline portions which they would like the teacher to read. Opinions vary on whether or not to give comments, especially ones that suggest corrections or a need for improvement; some teachers like to put comments on post-it notes so as to leave students work unmarked. Journals frequently are good sources of information about student's attitudes and misconceptions as well as emerging classroom problems. Teachers can often find out more about the students' thinking and degree of understanding from journals than from most other methods of assessment.
Observations, Interviews, and Conferences
Observations, interviews, conferences, and questions provide teachers and students with numerousopportunities to assess progress. At the heart of these types of assessment is the student and teacher working in collaboration in order to ascertain the progress the student has made. A student can analyze her or his own mathematical work by focusing on the quality of the product, the need for revision, changes or additions to be made, and different problemsolving strategies to employ. Performing an effective, critical analysis of one's work is a process that students can adapt for use later in life in their careers.
 |
SUGGESTIONS |
 Write observations on index cards or on a sheet of
address labels that can be transferred to student portfolios later.
Some teachers print up labels with names corresponding to the seating
chart so that it is easy to locate students.
Write observations on index cards or on a sheet of
address labels that can be transferred to student portfolios later.
Some teachers print up labels with names corresponding to the seating
chart so that it is easy to locate students.
 Give the same problem to the whole class but choose one or two
groups to observe closely.
Give the same problem to the whole class but choose one or two
groups to observe closely.
 Use a checklist of observation details for each group of
students. Rate each group (or simply check if you see the behavior)
on such items as whether all members are participating, whether they
are estimating before computing answers, whether they are using more
than one process, whether they are recording their work, whether they
are reporting their work, and whether they evaluate themselves.
Use a checklist of observation details for each group of
students. Rate each group (or simply check if you see the behavior)
on such items as whether all members are participating, whether they
are estimating before computing answers, whether they are using more
than one process, whether they are recording their work, whether they
are reporting their work, and whether they evaluate themselves.
Seminars, Labs, and Extended Projects
Assessment may also include student presentations (seminars), labs, and extended projects, particularly in the higher grades. These methods assure the connection between instruction and assessment as well as provide opportunities for relating mathematics to other subject areas. These methods are especially appropriate for assessing students' ability to identify and define a problem and what they already know; to make a plan; to create and modify problem-solving strategies; to collect, organize, and analyze needed information; to discuss, review, revise, and explain results; to persist in work on a problem; and to produce a quality product or report. Possible topics for these types of assessment might include maps, gears and ratios, sound waves and music, traffic patterns, collecting and analyzing litter, studying local water use, census studies, lunch preferences, sports statistics, plant growth, measurement of parts of the body, or nutrition.
The following are a sample of projects assigned to high school students at Glassboro High School. All projects involve a final presentation to the class, either in person or on videotape. Sophomores must complete three of the following:
- Plan a Day Trip to an Amusement Park
- Redecorate This Classroom
- Origami/Tangrams
- Logic Puzzles
- Conduct and Evaluate a Survey
- Menu Planning
- Chores
- Consumer Reports
More specific detail is provided for each choice. For example, for Consumer Reports, students are told:
Research an item you are considering purchasing in the near future by reviewing the ratings given all makes of this product by a consumer periodical such as Consumer Reports. Demonstrate to the class how to read the charts and what each symbol means. Research the actual cost locally of the three highest-rated makes. Choose one and justify your choice.
Seniors must complete one of the following projects, providing status reports at two points.
- Start Your Own Business (cost projections, loan application, graph of costs and income)
- Buy a Home (financing options, loan application, taxes)
- Design Your Dream Home (scale model, costs)
- Develop a Financial Plan for College or Other Post-Secondary Education (compare costs at four institutions, financial aid application)
- Plan a Community Service Project (survey, cost projections, grant application)
- Simulate Applying for and Getting Your First Post-HS Job and Plan Your Budget for the First Year at this Job
- Plan a Vacation for a Group of Five People for Two Weeks
|
Math In The News Susan Simon of Morris Knolls High School gives students in a high school discrete math course an article from a newspaper or magazine on a mathematical topic (such as Andrew Wiles' proof of Fermat's Theorem, DNA, or the Traveling Salesman Problem), and asks them to find two other sources on that topic, write a 3-page paper, and present the information to the class. |
Creating opportunities on a regular basis to observe, interview, confer, and question students while at work on their products is an essential component. Strategies such as think alouds, planned conferring periods, dialogue notebooks, and team notebooks afford both teachers and students with the opportunity to investigate student thinking.
The Student's Role in Assessment
The remaining cumulative progress indicators addresses an area that gets far too little attention - the students' role in assessment. The conventional perspective is that the student plays a passive role, simply answering questions or performing activities so that the instructor can evaluate his or her work. This standard calls for the student to play a more active role in assessment - to engage in self-assessment, to better communicate mathematical understanding, knowledge, and attitudes, and to use assessments as opportunities for reflection and growth.
5. Engage in ongoing assessment of their work to determine the effectiveness of their strategies and the correctness of their results.
6. Understand and accept that the criteria used to evaluate their performance will be based on high expectations.
7. Recognize errors as part of the learning process and use them as opportunities for mathematical growth.
8. Select and use appropriate tools effectively during assessment activities.
9. Reflect upon and communicate their mathematical understanding, knowledge, and attitudes.
"If students are to function as independent learners, they must reflect on their progress, understand what they know and can do, be confident in their learning, and ascertain what they have yet to learn" (NCTM Assessment Standards for School Mathematics, p. 14). Clearly, the student who wrote the following journal entry is an independent learner who can reflect on work in progress, knows what she is able to do, has confidence in what she does, and has the ability and practice to determine what she still needs to learn.
|
From a Sophomore Student's Mathematics Journal Entry In the past whenever we were evaluated in class, it was a day where no learning seemed to take place. I'd spend the night before looking over the problems we had been solving in class since the last test. I'd prepare as best I could by looking to see if there were some patterns to the problems. I'd come to class not really sure of what I knew and just hoping I'd pass. This year, I have trouble telling when I'm being "tested!" It all seems so connected. I've never been asked to create ways to test what I know and how I know. By keeping a dialogue notebook with my partner Sarah and my teacher, Mr. Cray, where I discuss what and how I'm learning, I've made some important discoveries. For example, one thing I've discovered about how I learn is that it helps if I can see what the written problem looks like. At first I was kind of intimidated by the graphing calculator. For example, I really had a lot of trouble understanding what Mr. Cray meant by the yintercept. It wasn't until he had us graph y=x, y=x+5, and y=x2, that I could see it. It was so clear! By using the calculator I can construct a lot more graphs to observe than I can by hand. As Mr. Cray always says, "When you find something that works for you, put it in your tool box." Making sense through pictures works for me. I think that the more I use pictures to help me learn new concepts, the less I will need to use pictures in the future. I can already see that I don't need to see certain graphs anymore, because I can picture them accurately in my head. I also appreciate being able to demonstrate my knowledge, even when I'm really unsure of what I know. I find that by talking with Sarah, or other members of my team, I can begin to discover what I'm learning. |
Seamless, connected instruction and assessment help to ensure learning and to make it more authentic, more real. In this journal entry, the student is responsible for selfassessment. She is able to be reflective because a system is in place to afford her the opportunity to practice regular inquiry. Through the use of a dialogue notebook, she is able to "discuss" with a partner and the teacher what she is learning and how she is learning. Important discoveries are made when students are afforded both time and strategies to delve into big questions such as: How do I make sense? What do I do when I don't know or understand? What tools do I have and use to help me make sense? How can I repeat success? Although not specific to mathematics, such questions form the basis of all learning. Knowing how one thinks and what one does when challenged with unfamiliar tasks or an unfamiliar method of inquiry is critical for all mathematics students.
 |
SUGGESTIONS |
 For problem-solving activities, have students complete a
self-assessment form such as the following one from Stenmark (1991,
p. 58).
For problem-solving activities, have students complete a
self-assessment form such as the following one from Stenmark (1991,
p. 58).
|
Problem-Solving Strategy Inventory Think about your use of strategies when solving the problem and check the following that apply.
1. ____ I didn't think about using strategies at all.
7. I tried the following strategies: |
 Use bookmarks for a weekly self-grading system. Have students
give themselves a grade each day for classwork and for homework on one
side of the card. On the other side, have them fill in responses to
questions such as the following:
Use bookmarks for a weekly self-grading system. Have students
give themselves a grade each day for classwork and for homework on one
side of the card. On the other side, have them fill in responses to
questions such as the following:
-
The thing I enjoyed most in math this week was ______________.
I am most proud of __________________________.
One thing I didn't like was ___________________.
I wish ____________________________________.
Collect the bookmarks on Fridays and distribute new ones on Mondays. Monitor responses, looking for patterns of learning for students. Give students feedback individually, perhaps through interviews.
 Have students assess their work as a group during cooperative
learning activities. You may wish to develop a form similar to the
one shown on the next page.
Have students assess their work as a group during cooperative
learning activities. You may wish to develop a form similar to the
one shown on the next page.
|
Group Assessment Names: |
|||
| Did your group: |  |
 |
 |
1. listen?  |
|||
2. talk about the task?  |
|||
3. cooperate?  |
|||
4. suggest good ideas?  |
|||
5. finish the task?  |
|||
What went well? |
|||
What do you wish you had done in a different way? |
|||
Educational Purposes of Assessment
The NCTM Assessment Standards for School Mathematics presents four categories of educational purposes for assessment: making instructional decisions, monitoring students' progress, evaluating individual students' achievement, and evaluating programs. These four categories are discussed in separate sections below.
A particular assessment task or instrument may well serve more than one of these purposes, but would be unlikely to be able to serve them all. An individual, teacher-administered, student interview designed to probe a third grader's understanding of place value and number base ideas, for example, could certainly help to make instructional decisions and to evaluate individual student achievement, but would be unlikely to be able to help evaluate the mathematics program as a whole. A nationally-normed, standardized test, on the other hand, if consistent with these standards and vision of mathematics education, can certainly help to evaluate the effectiveness of the educational program, but would be of limited value in making instructional decisions about individual students.
Making Instructional Decisions
Teachers gather assessment data continuously in order to ascertain how effective their teaching has been and to make changes in what and how they teach. Through observation, questioning, and student products, teachers are able to judge the effectiveness of their instruction. The judgments then form the basis for decisions about immediate and future instructional activity. Longrange, shortrange, and momenttomoment planning are all interconnected. The teacher who creates a longrange plan that spans a year includes specific benchmarks that can be used at intervals to mark students' progress. In addition, the momenttomoment instructional decisions that are made each day in the classroom are influenced by knowledge of the longrange and shortrange plans. More formal types of assessments are usually used for longer-range decisions, however, and more informal strategies for shorter-range decisions.
Longrange planning involves using assessment to help make decisions about a full year or semester of instruction. A critical component in these assessments is the determination of the most important mathematics to be learned during the period. Assessments are then tailored to create the data that best reveal students' understanding of this mathematics. Many teachers are beginning to use portfolios of student work to inform their long-range planning decisions. Others are using performance tasks that tend to require student integration of the content covered during a particular period of time.
Shortrange planning involves using assessments to influence the students' educational activity throughout a unit. Teachers review their long-range plans and the previous assessments in order to create a unit of study that will call on students' background knowledge to help them construct new knowledge. In an effort to gauge how well students are acquiring this new knowledge, teachers establish benchmarks within the unit of study. These benchmarks are assessments that help the teacher monitor student progress. Often-used strategies for making these kinds of instructional decisions are think-alouds, journal entries, student interviews, and short pencil-and-paper instruments.
Using assessments to influence momenttomoment decisions about instruction involves observing and listening to students while they are engaged in ordinary classroom activity. Such assessments happen continuously in most classrooms. Often teachers need to probe in order to truly understand what sense their students are creating. As a result, they frequently revise their plans based on the new informationthey have gleaned. Central to momenttomoment planning is the recognition that a longrange plan and specific benchmarks are clearly in place. Knowledge of both influences the daily decision making. The following vignette describes a teacher who finds think-alouds useful for daily decision-making in a second-grade class.
|
Think-Alouds Mrs. Seeliger, a second grade teacher, uses the technique of a think-aloud with her students in order to learn how they problem solve. "In order to see how my students are understanding new concepts, constant assessment is required. At this age, my students are changing rapidly and how they understood something yesterday is no guarantee as to how they'll respond today. As a result, I use think-alouds frequently. The children love to be verbal, so talking aloud while they think through a problem is something they enjoy. This technique helps me to hear what the children are thinking and to hear how they are problem solving. Such insights help me to see what changes I need to make in order to teach better." |
These moment-to-moment decisions come most effectively as a result of rich, fruitful classroom discussion. The more students are actively engaged in the exploration of a particular topic, the more evident will be their level of understanding and the more natural it will be for the teacher to slightly alter course. The NCTM Professional Standards for Teaching Mathematics (1991, p. 35) provide direction in how to promote this kind of productive discussion in the classroom. In discussing the teacher's role in discourse, the following suggestions are made:
 |
SUGGESTIONS |
 Pose questions and tasks that elicit, engage, and challenge each
student's thinking.
Pose questions and tasks that elicit, engage, and challenge each
student's thinking.
 Listen carefully to students' ideas.
Listen carefully to students' ideas.
 Ask students to clarify and justify their ideas orally and in
writing.
Ask students to clarify and justify their ideas orally and in
writing.
 Decide what to pursue in depth from among the ideas that
students bring up during a discussion.
Decide what to pursue in depth from among the ideas that
students bring up during a discussion.
 Decide when and how to attach mathematical notation and language
to students' ideas.
Decide when and how to attach mathematical notation and language
to students' ideas.
 Decide when to provide information, when to clarify an issue,
when to model, when to lead, and when to let a student struggle with a
difficulty.
Decide when to provide information, when to clarify an issue,
when to model, when to lead, and when to let a student struggle with a
difficulty.
 Monitor students' participation in discussions and decide
when and how to encourage each student to participate.
Monitor students' participation in discussions and decide
when and how to encourage each student to participate.
Monitoring Student Progress
The process of using assessments to monitor student progress is similar to that for making instructional decisions in that longrange, shortrange, and daily components need to be considered. However, the emphases of the two processes are different. When using assessments to plan instruction, the emphasis is on examining data in order to create units of study. When monitoring student performance, the focus is onunderstanding what sense students are making of the mathematics. Monitoring student progress successfully requires good communication between the students and the teacher. The following vignette demonstrates one strategy for monitoring student progress throughout a unit.
|
Well, What Do You Know? At the beginning of a new unit of study, I have students list in their notebooks everything they know and want to know about the general topic we will be studying. Next, the children share aloud what they know and want to know, as I record their findings on an overhead transparency. As a class we then take an inventory of what we know collectively. I ask students who volunteered pieces of information to share their knowledge with the class by elaborating on what they said. This process helps to build knowledge for those students who did not know the particular pieces of information. In addition, the children then clarify those items they want to know about. I include their selfgenerated list of information and ideas they wish to explore in my unit plan. This process of naming what we know and what we want to know better prepares us to learn any new information. Throughout the unit, I invite the students to return to their list of what they know and want to know in order to add additional information about what they now know and to clarify what they still want to know. This process helps me to make changes in the content I teach and especially in the sequence of activities I design. |
Evaluating Student Achievement
Teachers use a variety of assessment methods to gather evidence about students' learning and then provide feedback to the students about their progress. Students need to understand clearly not only what is expected but also whether their work is of acceptable quality. "For assessment to be equitable and valid, each student must received feedback over time on multiple occasions and in multiple formats on tasks that address the breadth of important mathematical content." (NCTM Assessment Standards for School Mathematics, p. 34). While feedback may be oral or written, formal or informal, private or public, geared toward an individual or a group, it should be always be descriptive, specific, relevant, timely, and encouraging.
Reports of student achievement indicate a student's demonstrated mathematical accomplishments at a specific moment in time. These reports may be grades based on a teacher's judgments about the student's understanding, scores from exams, checklists of competencies mastered by the student, or narrative reports of student progress. In each case, the purpose is to compare the student's progress with the goals he or she was expected to have achieved.
Evaluations of student achievement have three important characteristics, regardless of their form. First, they are summative and cannot be adjusted or changed. Second, they are designed to inform audiences beyond the classroom walls about the performance of individual students or groups of students. Finally, these evaluations are often used to make important decisions for students, such as admission, placement, or certification.
Grades should reflect each student's level of mathematical understanding rather than reflecting their comparative performance. They should be based on evidence that accurately reflects the progress of each student toward the attainment of mathematical power. They should indicate understanding of importantmathematical content, and they should be derived from learning situations in which students are actively engaged. When assessment is based on multiple sources of evidence, a single letter or number grade cannot adequately represent the breadth and depth of information about what students know, what they can do, and their disposition toward mathematics. Thus, these grades must be used with caution and with an awareness that much information is lost during the process.
The NCTM Assessment Standards for School Mathematics describes a comprehensive performance assessment system designed to document student achievement by using checklists, portfolios, and summary reports. The checklist provides information about student progress in mastering specific content and is completed based on a variety of assessment tasks, including observation. The portfolio is compiled by the student to demonstrate their understanding. The Summary Report provides information to parents and others outside the classroom; in it, the teacher summarizes student achievement by providing ratings for the checklist, portfolio, and progress.
| SUMMARY REPORT OF MATHEMATICAL THINKING | ||||||
| Checklist | Portfolio | Progress | ||||
| Developing as expected | Needs development | Developing as expected | Needs development | Developing as expected | Needs development | |
| Approach to mathematical thinking | ||||||
| Patterns & relationships | ||||||
| Number concepts & operations | ||||||
| Geometry & spatial relations | ||||||
| Measurement | ||||||
| Probability & statistics | ||||||
Evaluating Programs
A program evaluation uses information about student performance, along with other evidence, to judge the quality and success of the instructional program. Data on student achievement may be used for making modifications to a program or for making decisions about continuing a program. However, in addition to student achievement data, program evaluations should take into consideration information about goals,curriculum materials, instructional methods, students' opportunity to learn, and the responsibilities of teachers and administrators. This section of this chapter focuses only on the use of student achievement data in program evaluation.
A major distinction between the use of assessment data for program evaluation and for other purposes is that decisions can be made using results from groups of students. Statistical methods such as matrix sampling make it possible to expand the scope and types of tasks that can be administered to students, since not all tasks need be completed by all students. Short-answer or multiple-choice tests can elicit some information on skills if the balance among topics is appropriate for the intended purpose. Performance assessment tasks can provide other types of information, especially concerning problem solving, reasoning, communication, mathematical connections, and use of tools and technology.
It is important to recognize that the relevant information an assessment can provide is limited by the choice of question formats. For example, multiple-choice questions are poorly suited to furnishing information about problem solving and mathematical communication. Similarly, using a performance task to ascertain whether students know their addition facts is inefficient. Any single form of assessment often limits the scope of what is being tested to what fits that format. It is important to incorporate a variety of assessment methods into any program evaluation to ensure that the full spectrum of mathematical content is addressed.
Many large-scale tests unfortunately report too little information to be useful in evaluating programs. For example, at the district level, only the average percentile ranking for students in mathematics may be available. This information does not indicate the range or distribution of student scores - for example, are scores low because of a few very low-achieving students or because most students are achieving at slightly below-average levels? Nor does it provide information about the specific content areas in which the instructional program may have strengths or weaknesses. It may be necessary to provide more detailed information in order to determine, for example, whether an instructional program is adequately serving both the gifted and the low-achieving student.
New Jersey's Mathematics Standards can be used as yardsticks, as measurement tools, against which school mathematics programs can and should be measured. Data should be collected to enable reviewers to determine the extent to which each of the standards, each of the recommendations of the Framework, and each other local objective, is being met.
The Assessment Process
The material in this section is taken from the NCTM Assessment Standards for School Mathematics.
"The assessment process can be thought of as four interrelated phases that highlight points at which critical decisions need to be made. The figure below shows the four phases - plan the assessment, gather evidence, interpret the evidence, and use the results. The division is arbitrary however, and makes the process seem more orderly that it actually is. In practice the phases are interactive, and the distinctions between them are blurred. Assessment does not proceed through them in a neat, linear fashion.
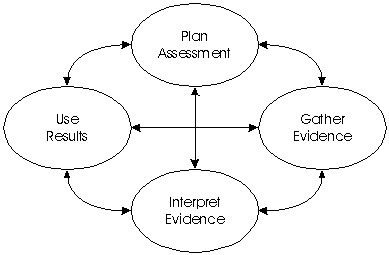
"Each phase of the assessment process can be characterized by the decisions and actions that occur with that phase as follows:
Plan Assessment
- What purpose does the assessment serve?
- What framework is used to give focus and balance to the activities?
- What methods are used for gathering and interpreting evidence?
- What criteria are used for judging performance on activities?
- What formats are used for summarizing judgments and reporting results?
Gather Evidence
- How are activities and tasks created or selected?
- How are procedures selected for engaging students in the activities?
- How are methods for creating and preserving evidence of the performances to be judged?
Interpret Evidence
- How is the quality of the evidence determined?
- How is an understanding of the performances to be inferred from the evidence?
- What specific criteria are applied to judge the performance?
- Have the criteria been applied appropriately?
- How will the judgments be summarized as results?
Use Results
- How will the results be reported?
- How should inferences from the results be made?
- What action will be taken based on the inferences?
- How can it be ensured that these results will be incorporated in subsequent instruction and assessment?
"The phrase assessment process ... emphasizes the complex process that underlies the purposes for which assessments are done, the decisions made by the assessors, and the standards to which assessments are held. This vision of assessment should apply to any assessment purpose."
SUMMARY
As New Jersey's Mathematics Standards are implemented in classrooms throughout the state, assessment changes will also be implemented, corresponding to the curricular and instructional choices that are made. Students will experience a wide variety of assessment methods and will become more informed and active participants in the assessment process. The goals and purposes of assessment will be considered as assessments are constructed, implemented, and revised, and as the results of assessment are used in making instructional decisions, monitoring student progress, evaluating student achievement, and evaluating programs. Each of the changes outlined in this chapter represents a shift along a continuum toward improved practice. These shifts are summarized in the following table, highlighting important ideas involving assessment.
| Major Shifts in Assessment Practice | |
| Toward ... | Away From ... |
| Assessing students' full mathematical power | Assessing only students' knowledge of specific facts and isolated skills |
| Comparing students' performance with specific performance criteria | Comparing students' performance with that of other students |
| Giving support to teachers and credence to their informed judgment | Designing "teacher-proof" assessment systems |
| Making the assessment process public, participatory, and dynamic | Making the assessment process secret, exclusive, and fixed |
| Developing a shared vision of what to assess and how to do it | Developing assessment by oneself |
| Using assessment results to ensure that all students have the opportunity to achieve their potential | Using assessment to filter and select students out of the opportunities to learn mathematics |
| Aligning assessment with curriculum and instruction | Treating assessment as independent of curriculum or instruction |
| Basing inferences on multiple sources of evidence | Basing inferences on restricted or single sources of evidence |
| Viewing students as active participants in the assessment process | Viewing students as the objects of assessment |
| Regarding assessment as continual and recursive | Regarding assessment as sporadic and conclusive |
| Holding all concerned with mathematics learning accountable for assessment results | Holding only a few accountable for assessment results |
| Communicating with students about their performance in a continuous, comprehensive manner | Simply indicating whether or not answers are correct |
| Using multiple and complex assessment tools (such as performance tasks, projects, writing assignments, oral demonstrations, and portfolios) | Sole reliance on answers to brief questions on quizzes and chapter tests |
| Using evidence of every student's progress toward long-range goals in instructional planning | Planning for content coverage with little regard for students' progress |
| Making program decisions based on high-quality evidence from multiple sources | Relying on over-simplified evidence from a single test or test format |
Adapted from NCTM Assessment Standards for School Mathematics, p. 83.
References
-
DarlingHammond, L. "Performancebased assessment and educational equity." In Harvard Educational Review, 64 (1), 530, 1994.
Mathematical Sciences Education Board. National Research Council. Everybody Counts. Washington, DC: National Academy Press, 1989.
Mathematical Sciences Education Board. National Research Council. Measuring What Counts. Washington. DC: National Academy Press, 1993.
Mathematical Sciences Education Board. National Research Council. Measuring Up: Prototypes for Mathematics Assessment. Washington, DC: National Academy Press, 1993.
Meyer, C. A. "What's the difference between authentic and performance assessment?" Educational Leadership (49)8, 3930, 1992.
National Council of Supervisors of Mathematics. Great Tasks and More!!, A Source Book of Camera- Ready Resources on Mathematical Assessment: Reston, VA, 1996.
National Council of Teachers of Mathematics. Assessment Standards for School Mathematics. Reston, VA, 1995.
National Council of Teachers of Mathematics. Mathematics Assessment: Myths, Models, Good Questions, and Practical Suggestions. Reston, VA, 1991.
National Council of Teachers of Mathematics. Professional Standards for Teaching Mathematics. Reston, VA, 1991.
New Jersey State Department of Education. Mathematics Instructional Guide: Linking Classroom Experiences to Current Statewide Assessments. D. Varygiannes, Coord. Trenton, NJ, 1996.
New Jersey State Department of Education. Grade 11 High School Proficiency Test: Directory of Test Specification and Items, Trenton, NJ, 1992.
Stenmark, J. K., Ed. Mathematics Assessment: Myths, Models, Good Questions, and Practical Suggestions. Reston, VA: National Council of Teachers of Mathematics, 1991.
Wiggins, G. "Teaching to the (authentic) test." Educational Leadership 46(7), 4147, 1989.
Wiggins, G. "A True Test: Toward More Authentic and Equitable Assessment." Phi Delta Kappan 70, 703713, 1989.
On-Line Resources
-
http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/
The Framework will be available at this site during Spring 1997. In time, we hope to post additional resources relating to this standard, such as grade-specific activities submitted by New Jersey teachers, and to provide a forum to discuss the Mathematics Standards.