Combinatorial Geometry Open Problems
Index of Problems
Crossing Families
RESEARCHER: Pavel Valtr
OFFICE: CoRE 411
Email:valtr@dimacs.rutgers.edu
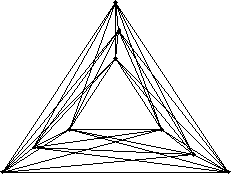
DESCRIPTION: Consider N points in the plane so that
no three points lie on a line. Draw a line segment between
each pair of vertices. The open problem is this: How large a family
of mutually crossing line segments must there be? We say two
line segments cross if they intersect on their interiors (as opposed
to at their
endpoints.) In the figure to the right, there is a family of 3
mutually crossing line segments, but not a family of 4.
It has been shown that there must always be a family of size
sqrt(N/12), but it is believed that there must always be families of much
larger size as well. So, what is the largest exponent t so
that among N points in the plane, no three on a line, one can always
find a crossing family of
at least cN^t line segments, for some fixed constant
c>0? If you can find
such a t bigger than 1/2, then you will have made a
substantial contribution.
Empty Hexagons
RESEARCHER: Pavel Valtr
OFFICE: CoRE 411
Email:valtr@dimacs.rutgers.edu
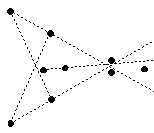
DESCRIPTION: It is known that any set of at least 10 points
in the plane, no three on a line, contains an empty pentagon
(i.e., 5 points which are vertices
of a convex pentagon whose interior contains none of the points).
The figure on the right shows 9 points with no empty pentagon (the dotted
lines are shown to help visualization).
Horton (1983) constructed arbitrarily large sets of points in the plane
with no "empty 7-gon". The following question of Erdos
remains open: "Is there an integer N such that
any set of at least N points in the plane, no three on a line,
contains an empty hexagon (i.e., six vertices of a convex hexagon
whose interior contains no point of the set)?" Could you at least find,
for any sufficiently large integer K, an empty hexagon
in any set of K^2 points in a square K by K, when the distance
between any two points is at least 1/10, say. This could be easier,
although there is an example of such restricted sets with
no empty heptagon.
Non-empty Strips
RESEARCHER: Pavel Valtr
OFFICE: CoRE 411
Email:valtr@dimacs.rutgers.edu
DESCRIPTION: Consider a set S of N^2 points inside a disk bounded
by a circle C of length N,
such that the distance between any two points of S is at least 1/100, say.
Let A be a set of N^2 points distributed equidistantly along C.
It is known that for at least c·N^4 pairs a,b of points of A,
there is a point of S at distance at most 1/N from the line ab
(c>0 is a positive constant). Is there a positive constant d>0 such that
for at least d·N^4 pairs a,b of points of A, there are at least two points
of S at distance at most 1/N from the line ab?
Back to main page