We model actions as transitions from states to states. If in state s the action
In the previous section we have proven our logic sound, so every theorem of the logic is a tautology in the model. This, however, does not by itself establish in any way the suitability of the logic as a tool for proving protocols correct. In fact, protocols were not referred to at all.
We model actions as transitions from states to states.
If in state s
the action ![]() is performed,
only the local states for P and Q will be changed.
The new state s' is the least (closed global) state such that
is performed,
only the local states for P and Q will be changed.
The new state s' is the least (closed global) state such that
![]() ,
, ![]() and
and ![]() .From the closure properties we know that the local states for other
principals stay unchanged. Formally:
.From the closure properties we know that the local states for other
principals stay unchanged. Formally:

Using Lemma 10 it follows immediately from the
definition of ![]() that the transition function
is augmenting for a fixed protocol:
that the transition function
is augmenting for a fixed protocol:
![]()
A specification of a protocol
is given by two sets of formulas, ![]() (the
assumptions) and
(the
assumptions) and ![]() (the conclusions).
Protocol
(the conclusions).
Protocol ![]() satisfies such a specification
(notation:
satisfies such a specification
(notation: ![]() )when ``
)when ``![]() holds initially'' guarantees that
``
holds initially'' guarantees that
``![]() holds finally'', i.e., after running
holds finally'', i.e., after running ![]() .We extend the relation
.We extend the relation ![]() between states and formulas to a relation
between states and sets of formulas, as follows:
between states and formulas to a relation
between states and sets of formulas, as follows:
![]()
Using this,
the semantics of the specification triple
![]() is now defined as follows:
is now defined as follows:
![]()
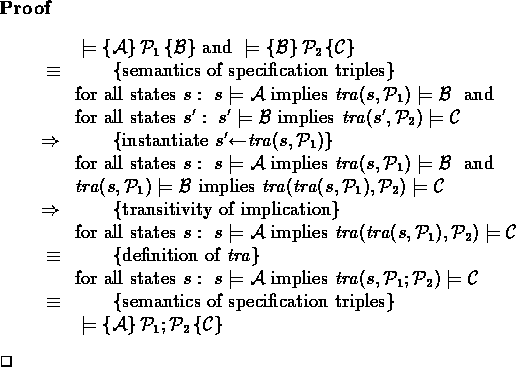
Similarly, one can prove: