Fast exponentiation algorithms

Suppose that you have to compute $S=m^s \bmod{n}$. If $s=\sum_{i=0}^{t-1}s_i 2^i$ is the binary decomposition of s , then this computation can efficiently be performed as depicted on Fig. 3. Indeed, if we respectively let $z^{(i)}$ and $y^{(i)}$ the values of z and y at step i (Lines 5 and 7 of Fig. 3), we have $z^{(i)}=z^{(i-1)}\left(y^{(i-1)}\right)^{s_{i-1}} \bmod{n}$ and $y^{(i)}=m^{2^i} \bmod{n}$. So,

 $$\begin{eqnarray} S &\equiv& m^{\mbox{}^{\sum_{i=0}^{t-1}s_i2^i}} \equiv \prod_{... ...=1}^t \frac{z^{(i)}}{z^{(i-1)}} \equiv z^{(t)} \pmod{n}.\nonumber\end{eqnarray}$$

   Figure 3: Square-and-multiply method (I).

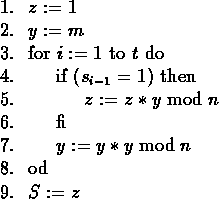
   Figure 4: Square-and-multiply method (II).

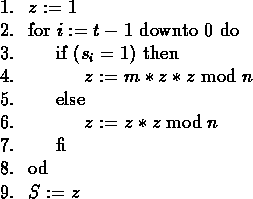
Scanning the bits of exponent s from left to right, we obtain another efficient algorithm to compute $S=m^s \bmod{n}$ (see Fig. 4). The drawback in this algorithm is that it cannot easily be parallelized. Consequently, we only focus on the first algorithm.