The following paper is also available as PostScript file.
John C. Mitchell, Vitaly Shmatikov, and Ulrich Stern
Computer Science Department, Stanford University, Stanford,
CA 94305
{mitchell,shmat,uli.stern}@cs.stanford.edu
August 1, 1997
In previous work [8],
a general-purpose finite-state analysis tool, Mur
[2],
has been successfully applied to the verification of small protocols such as
Needham-Schroeder, Kerberos, and TMN. In an effort to
understand the difficulties involved in analyzing larger and more
complex protocols, we use Mur to analyze the SSL 3.0 handshake
protocol. The choice of SSL 3.0 was determined by its size and relative
complexity as well as its current popularity as a de facto standard for
secure Internet communication.
In the process of studying the feasibility of SSL 3.0 verification by exhaustive state enumeration, we develop a ``rational reconstruction'' of the protocol. More specifically, after initially attempting to familiarize ourselves with the handshake protocol, we found that we could not easily identify the purpose of certain message fields (version number, nonce, etc.) in some steps of the protocol. Therefore, we set out to use our analysis tool to identify, for each field, an attack that could occur if that field were omitted from the protocol. The result of our study is an incremental presentation of the protocol, beginning with a simple, intuitive, and flawed protocol exchanging the required data, and culminating in a close approximation of the actual SSL 3.0 handshake protocol. Our final protocol does not have any errors identifiable by our exhaustive finite-state analysis.
In the process of conducting this study, we uncovered the major problems with SSL 2.0 that motivated the design of SSL 3.0. We are currently investigating various anomalies related to protocol resumption.
Another formal analysis of SSL 3.0, using a logic formalizing concepts of knowledge and belief, appears in [1]. We did not become aware of this other study until after we had completed our analysis.
Our general methodology for modeling security protocols
in Mur is outlined in our previous paper [8].
The basic approach is similar to the CSP approach to
model checking of cryptographic protocols outlined in [7, 9].
However, there are some differences between Mur and FDR.
verification system
Mur [2] is a
protocol verification tool that has been successfully
applied to several industrial protocols, especially in the
domains of multiprocessor cache coherence protocols and
multiprocessor memory models [3, 11, 12].
To use Mur for verification, one has to model the protocol
in the Mur language and augment this model with a
specification of the desired properties. The Mur system
automatically checks, by explicit state enumeration, if all
reachable states of the model satisfy the given specification.
For the state enumeration,
either breadth-first or depth-first search
can be selected. Reached states are stored in a hash
table to avoid redundant work when a state is revisited.
The memory available for this hash table typically determines
the largest tractable problem.
The Mur language is a simple high-level language for describing
nondeterministic finite-state machines.
Many features of the language
are familiar from conventional programming languages.
The main features not found in a
``typical'' high-level language are described in the following
paragraphs.
The state of the model
consists of the values of all global
variables. In a startstate statement, initial values are assigned to
global variables. The transition from one state to another is
performed by rules. Each rule has a Boolean condition and an
action, which is a program segment that is executed atomically.
The action may be executed if the condition is true
(i.e., the rule is enabled) and typically changes
global variables, yielding a new state.
Most Mur models are nondeterministic
since states typically allow execution of more
than one rule.
For example, in the model of the SSL protocol,
the intruder usually
has the nondeterministic choice of several messages
to replay.
Mur has no explicit notion of processes. Nevertheless
a process can be implicitly modeled by a set of related rules.
The parallel composition of two processes
in Mur is simply done by using the union of the rules of
the two processes.
Each
process can take any number of steps (actions) between the
steps of the other. The resulting computational model is that
of asynchronous, interleaving concurrency.
Parallel processes communicate
via shared variables; there are no special language constructs
for communication.
The Mur language supports scalable models.
In a scalable model,
one is able to change the size of the model by
simply changing constant declarations.
When developing protocols, one typically starts
with a small protocol configuration. Once this
configuration is correct, one gradually increases the protocol
size to the largest value that still allows verification to complete.
In many cases, an error in the general (possibly infinite state)
protocol will also show up in a down-scaled (finite state)
version of the protocol. Mur can only
guarantee correctness of the down-scaled version of the protocol,
but not correctness of the general protocol.
For example, in the model of the SSL protocol, the numbers of clients and
servers are scalable and defined by constants.
The desired properties of a protocol can be specified in
Mur by
invariants, which are Boolean conditions that have to be true
in every reachable state.
If a state is reached in which some invariant is violated,
Mur prints
an error trace - a sequence of states from the start state
to the state exhibiting the problem.
There are two main differences between Mur and FDR.
First, while communication is supported in FDR by the CSP notions of
channels and events, it is modeled by shared variables
in Mur . Second, Mur currently implements
a richer set of
methods for increasing the size of the protocols that
can be verified - consisting of both several
techniques to reduce the number of reachable states [6]
and several techniques to perform the state space search
more efficiently, reducing runtime and memory
requirements [10].
In outline, we have analyzed protocols using the following sequence of steps:
formulation of a protocol, however,
is more detailed than the high-level
descriptions often seen in the literature,
since one has to decide exactly which
messages will be accepted by each participant in the protocol.
Since Mur communication is based on shared variables,
it is also necessary to define an explicit message format,
as a Mur type.
The primary goal of the SSL 3.0 handshake protocol is to establish secret keys that ``provide privacy and reliability between two communicating applications'' [5]. Henceforth, we call the communicating applications the client (C) and the server (S). The basic approach taken by SSL is to have C generate a fresh random number (the secret or shared secret) and deliver it to S in a secure manner. The secret is then used to compute a so-called master secret (or negotiated cipher), from which, in turn, the keys that protect and authenticate subsequent communication between C and S are computed. While the SSL handshake protocol governs the secret key calculation, the SSL record layer protocol governs the subsequent secure communication between C and S.
As part of the handshake protocol, C and S exchange their respective cryptographic preferences, which are used to select a mutually acceptable set of algorithms for encrypting and signing handshake messages. In our analysis, we assume for simplicity that RSA is used for both encryption and signatures, and cryptographic preferences only indicate the desired lengths of keys. In addition, SSL 3.0 is designed to be backward-compatible so that a 3.0 server can communicate with a 2.0 client and vice versa. Therefore, the parties also exchange their respective version numbers.
The basic handshake protocol consists of three messages. With the client hello message, the client starts the protocol and transmits its version number and cryptographic preferences to the server. The server replies with the server hello message, also transmitting its version number and cryptographic preferences. Upon receipt of this message, the client generates the shared secret and sends it securely to the server in the secret exchange message.
Since we were not aware of any formal definition of SSL 3.0, we based our model of the handshake protocol on the Internet draft [5]. The draft does not include a precise list of requirements that must be satisfied by the communication channel created after the handshake protocol completes. Based on our interpretation of the informal discussion in Sections 1 and 5.5 of the Internet draft, we believe that the resulting channel can be considered ``secure'' if and only if the handshake protocol completes successfully (i.e., both parties reach the state in which they are ready to communicate using the negotiated cipher) and the following properties must hold after protocol completion:
be the number that C considers the shared secret,
and 
the number that S considers the shared secret.
Then and must be identical.
We propose that any violation of the foregoing invariants that goes undetected by the legitimate participants constitutes a successful attack on the protocol.
SSL 3.0 supports protocol resumption. In the initial run of the
protocol, C and S establish a shared secret by going through the
full protocol and computing secret keys that protect subsequent communication.
SSL 3.0 allows the parties to resume
their connection at a later time without repeating the full protocol.
If the client hello message
sent by C to S includes the identifier of an SSL
session that is still active according to S's internal state, the
server assumes that C wants to resume a previous session. No public
keys or secrets are exchanged in this case, but the master secret and
the keys derived from it are recomputed using new nonces. (See Section
4.8 for an explanation of how nonces are used in the protocol to
prevent replay attacks, and the Appendix to see how the
master secret is computed from the nonces and shared secret.) Our
Mur model supports protocol resumption.
Finally, it should be noted that whenever one of the parties detects an inconsistency in the messages it receives, or any of the protocol steps fails in transmission, the protocol is aborted and the parties revert to their initial state. This implies that SSL is susceptible by design to some forms of ``denial of service'' attacks: an intruder can simply send an arbitrary message to a client or server engaged in the handshake protocol, forcing protocol failure.
We start our incremental analysis with the simplest and most intuitive
version of the protocol and give an attack found by Mur . We then add
a little piece of SSL 3.0 that foils the attack, and let Mur discover
an attack on the augmented protocol. We continue this iterative process
until no more attacks can be found. The final protocol turns out to be
a stripped-down version of SSL 3.0.
The following notation will be used throughout the paper.
In general, our model assumes perfect cryptography. The following list explains what this assumption implies for all cryptographic functions used in SSL.
, only party i can learn x. (This is only
true iff the private key 
is not available to any party except
i. This is a safe assumption, given that no participants in the SSL
handshake protocol are ever required to send their private key over the
network.) The intruder may, however, store the entire encrypted message
and replay it later without learning x. The structure of the
encrypted message is inaccessible to the intruder, i.e., it cannot split
the encrypted message into parts and insert them into other encrypted
messages.
can only be generated by the
party i. Anyone who possesses i's verification key 
is able to
verify that the message was indeed signed by i. We assume that
signatures do not encrypt. Therefore, x can be learned by anyone.
, it is not computationally feasible to
find any x' such that
.
In protocols, it is therefore assumed that
a participant can determine whether x=x' by
comparing to
.
,
and are thus able to verify messages signed by CA. Every party
i is assumed to possess CA-signed certificates for its own
public keys: 
(certifying that public encryption key 
indeed belongs to i)
and 
(certifying that
public verification key indeed belongs to i).
The first step of the basic protocol consists of C sending information about its identity, SSL version number, and cryptographic preferences (aka cryptosuite) to S. Upon receipt of C's hello message, S sends back its version, cryptosuite (S selects one set of algorithms from the preference list submitted by C), and its public encryption key. C then generates a random secret and sends it to S, encrypted by S's public key.
Notice that the first hello message (that from C to S) contains the identity of C. There is no way for S to know who initiated the protocol unless this information is contained in the message itself (perhaps implicitly in the network packet header).
Protocol A does not explicitly (and securely) associate the server's name with its public encryption key. This allows the intruder to insert its own key into the server's hello message. The client then encrypts the generated secret with the intruder's key, enabling the intruder to read the message and learn the secret.
To fix the bug in Protocol A, we add verification
of the public key.
The server now sends its public key 
in a
certificate signed by the certificate authority. As
described before, the certificate has the following form:
.
We assume that signatures are unforgeable. Therefore, the intruder will
not be able to generate 
. The intruder may send the certificate for its own public key
, but the client
will reject it since it expects S's name in the certificate. Finally,
the intruder may generate 
, but the client expects a message signed by CA, and
will try to verify it using CA's verification key. Verification
will fail since the message is not signed by CA, and the client
will abort the protocol. Notice that SSL's usage of certificates to
verify the server's public key depends on the trusted certificate authority
assumption (see Section 4.2 above).
Protocol B includes no verification of the client's identity. This allows the intruder to impersonate the client by generating protocol messages and pretending they originate from C. In particular, the intruder is able to send its own secret to the server, which the latter will use to compute the master secret and the derived keys.
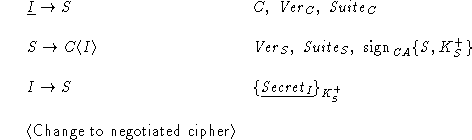
To fix the bug in Protocol B, the server has to verify that the secret it received was indeed generated by the party whose identity was specified in the first hello message. For this purpose, SSL employs client signatures.
The client sends to the server its verification key in the
CA-signed certificate 
. In addition, immediately after sending its secret
encrypted with
the server's public key, the client signs the hash of the secret
and sends it to the
server. Hashing the secret is necessary so that the intruder will not
be able to learn the secret even if it intercepts the message. Since
the server can learn the secret by decrypting the client key exchange
message, it is able to compute the hash of the secret and compare it
with the one sent by the client.
Notice that the server can be assured that 
is indeed C's
verification key since the intruder cannot insert its own key in the
CA-signed certificate assuming that signatures are unforgeable. Therefore, the server
will always use to verify messages ostensibly signed by the
client, and all messages of the form 
will be rejected. Even if the intruder were able to generate
the message 
, the attack
will be detected when the server computes 
and discovers
that it is different from 
.
Instead of signing the hashed secret, the client can sign the secret directly and send it to the server encrypted by the server's public key. The SSL definition, however, does not include encryption in this step [5, Section 5.6.8,]. We used hashing instead of encryption as well since we intend our incremental reconstruction of SSL to follow the definition as closely as possible. The exact reason why the designers of the protocol chose to rely on hashing rather than encryption to protect the secret is unclear to us.
It is interesting to note that SSL 2.0 has several problems in the client authentication stage. It uses the same key for verification and encryption, while the approach outlined above allows the verification key to be longer (and thus, hopefully, more secure) than the encryption key. Also, the strength of the verification key in SSL 2.0 is independent of the cryptographic preferences.
Even though the intruder cannot modify keys and shared secrets in Protocol C, it is able to attack the plaintext information transmitted in the hello messages. This includes the parties' version numbers and cryptographic preferences.
By modifying version numbers, the intruder can convince an SSL 3.0 client that it is communicating with a 2.0 server, and a 3.0 server that it is communicating with a 2.0 client. This will cause the parties to communicate using SSL 2.0, giving the intruder an opportunity to exploit any of the known weaknesses in SSL 2.0.
By modifying the parties' cryptographic preferences, the intruder can force them into selecting a weaker encryption and/or signing algorithm than they normally would. This may make it easier for the intruder to decrypt the client's secret exchange message, or to forge the client's signature. It is interesting to note that the SSL 2.0 protocol is susceptible to this ``dumbing down'' attack.
The parties can prevent attacks on plaintext by repeating the exchange of versions and cryptographic preferences once the handshake protocol is complete; the additional messages will be called verification messages. Since the intruder cannot learn the shared secret, it cannot compute the master secret and the derived keys and thus cannot interfere with the parties' communication after they switch to the negotiated cipher.
Suppose the intruder altered the version number or cryptographic preferences in the client's hello message. When the client sends its version and cryptosuite to the server under the just negotiated encryption, the intruder cannot change them. The server will detect the discrepancy and abort the protocol. This is also true for the server's version and cryptosuite.
In Protocol D, the parties verify only plaintext information
after the handshake negotiation is complete. Since the intruder cannot
forge signatures, invert hash functions, or break encryption without the
correct private key, it can neither learn the client's secret, nor
substitute its own. It may appear that D provides complete
security for the communication channel between C and S. However,
Mur discovered an attack on client's identity that succeeds even if
all cryptographic algorithms are perfect.
Intruder I intercepts C's hello message to server S, and initiates the handshake protocol with S under its own name. All messages sent by S are re-transmitted to C, while most of C's messages, including the post-handshake verification messages, are re-transmitted to S. (See the protocol run below for details. Re-transmission of C's verification message is required to change the sender identifier, which is not shown explicitly below.) As a result, both C and S will complete the handshake protocol successfully, but C will be convinced that it is talking to S, while S will be convinced that it is talking to I.
Notice that I does not have access to the secret shared between C and S. Therefore, it will not be able to generate or decrypt encrypted messages after the protocol is complete, and will only be able to re-transmit C's messages. However, the server will believe that the messages are coming from I, whereas in fact they were sent by C.
This kind of attack, while somewhat unusual in that it explicitly reveals the intruder's identity, may prove harmful for a number of reasons. For example, it deprives C of the possibility to claim later that it communicated with S, since S will not be able to support C's claims (S may not even know about C's existence). If S is a pay server providing some kind of online service in exchange for anonymous ``electronic coins'' such as eCash [4], I may be able to receive service from S using C's cash. Recall, however, that I can only receive the service if it is not encrypted, which might be the case for large volumes of data.
To fix the bug in Protocol D, the parties verify all of their communication after the handshake is complete. Now the intruder may not re-transmit C's messages to S, because C's hello message contained C, while the hello message received by the server contained I. The discrepancy will be detected in post-handshake verification.
I observes a run of the protocol and records all of C's messages. Some time later, I initiates a new run of the protocol, ostensibly from C to S, and replays recorded C's messages in response to messages from S. Even though I is unable to read the recorded messages, it manages to convince S that the latter is talking to C, even though C did not initiate the protocol.
Next run of the protocol ...
By adding random nonces to each run of the protocol, we make sure that there are always some differences between independent runs of the protocol. The intruder is thus unable to replay verification messages from one run in another run.
The exact semantics of the verification messages exchanged after
switching to the negotiated cipher (i.e., Finished messages in
the SSL terminology) is somewhat unclear. Section 5.6.9 of [5]
states: ``No acknowledgment of the finished message is required;
parties may begin sending encrypted data immediately after sending the
finished message. Recipients of finished messages must verify that the
contents are correct.'' The straightforward implementation of this
definition led Mur to discover the following attack on Protocol
F:
as it is being
transmitted from C to S. .
Since we did not model weak encryption that can be broken by the intruder, we also did not model the last step of the attack explicitly. Instead, if the model reached the state after the 3rd step, the attack was considered successful.
To prevent the attack on Protocol F, it is sufficient to require
that the parties consider the protocol incomplete until checking
verification messages they received from each other. Mur did not
discover any bugs in the model implemented according to this semantics.
Alternatively, yet another piece of SSL can be added to Protocol F. If the client sends the server a hash of all messages before switching to the negotiated cipher, the server will be able to detect an attack on its cryptosuite earlier.
Mur was used to model Protocol G with 2 clients, 1 intruder, 1
server, no more than 2 simultaneous open sessions per server, and no
more than 1 resumption per session. No bugs were discovered. We
are currently investigating several protocol resumption anomalies
related to the version rollback attack.
Following is the definition of the SSL 3.0 handshake protocol according to [5]. When several messages from the same party follow each other in the original definition, they have been collapsed into a single protocol step (e.g., Certificate, ClientKeyExchange, and CertificateVerify were joined into ClientVerify). The underlined pieces of SSL 3.0 are not in Protocol G.
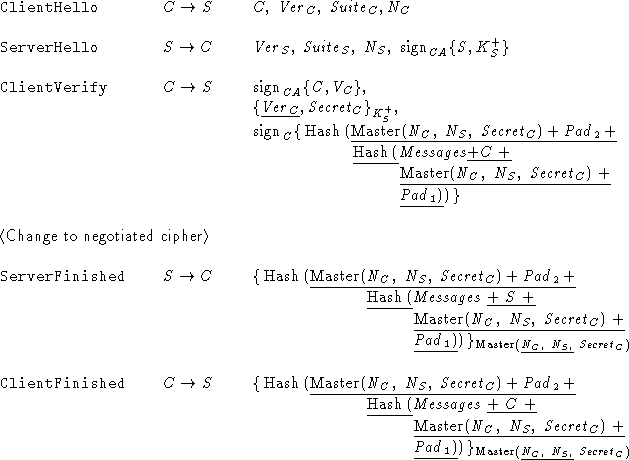
for protocol verificationWhile the main goal of our analysis was ``rational reconstruction'' of the SSL 3.0 handshake protocol, we were also interested in lessons to be learned about using finite-state analysis to verify large protocols. We were particularly concerned about the potentially very large number of reachable states, given that the SSL handshake protocol consists of 7 steps, and each message sent in a particular step includes several components, each of which can be changed by the intruder under certain conditions.
Our model of the intruder is very simple and straightforward. There is no intrinsic knowledge of the protocol embedded in the intruder, nor does the design of the intruder involve any prior knowledge of any form of attack. The intruder may monitor communication between the protocol participants, intercept and generate messages, split intercepted messages into components and recombine them in arbitrary order. No clues are given, however, as to which of these techniques should be used at any given moment. Therefore, the effort involved in implementing the model of the intruder is mostly mechanical.
The following simple techniques proved useful in reducing the number of states to be explored:
explored were identical as far as the state of the legitimate
participants was concerned and the only difference was the contents of the
intruder's database. By ensuring that the database is always as full as
it can possibly be (i.e., it includes all knowledge that can be
extracted from the messages transmitted on the network thus far), we
achieved an order of magnitude reduction in the number of reachable states
(e.g., from approximately 200,000 to 5,000 for a single run of the
protocol).
Running under Linux on a Pentium-120 with 32MB of RAM, the model takes approximately 1.5 minutes to check for the case of 1 client, 1 server, 1 open session, and no resumptions. Less than 5000 states are explored.
The largest instance of our model that we verified included 2 clients, 1 server, no more than 2 simultaneous open sessions per server, and no more than 1 resumption per session. Checking took slightly under 8 hours, with 193,000 states explored.
The SSL 3.0 master secret is computed in the following way.
verification system.
In Computer Aided Verification. 8th International Conference,
pages 390-3, 1996.
.
In IEEE Symposium on Security and Privacy, pages 141-51, 1997.
-I.
In 32nd Design Automation Conference, pages 7-12, 1995.
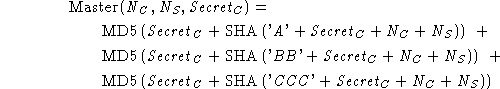
Finite-State Analysis of SSL 3.0 and Related Protocols
This document was generated in part using the LaTeX2HTML translator Version 96.1 (Feb 5, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.