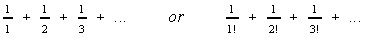High school students build upon their knowledge of rational numbers as they increase their understanding of irrational numbers and generalize number relationships through their work with algebra. The key components of number sense, as identified in the K-12 Overview, are an awareness of the uses of numbers in the world around us, a good sense of approximation, estimation, and magnitude, the concepts of numeration, and an understanding of the equivalence of different representations and forms of numbers.

In their work with numeration, ninth- through twelfth-graders should view mathematics as a coherent body of knowledge. They should see the integers, the rational numbers, and the real numbers as logical and necessary extensions of the whole number system. Only with these extensions can expressions like 3 minus 7, 4 divided by 3, and the ratio of the circumference of a circle to its diameter have values. High school students should understand how the integers, rational numbers, irrational numbers, and real numbers are related to each other and what properties are true for the numerical operations on these number systems.

Students at these grade levels continue their learning about equivalence, but with an increasing focus on approximation, particularly for irrational numbers (see Standard 14 - Building Blocks of Calculus). High school students should understand the difference between an exact value of an irrational number, such as sqrt(3), and its approximation (1.728). They should also be familiar with the use of scientific notation as an equivalent form of decimal number.

Estimation continues to be a regular part of mathematics classes, both estimation of quantities and estimation of the results of operations. Students should respond to questions that arise naturally during the course of the class with answers that illustrate confident and well-conceived use of estimation strategies and number sense.

Technology also plays an important role in number sense at these grade levels, particularly since calculators and computers use approximations for some fraction-to-decimal conversions and for irrational numbers. Calculators can be wonderful exploration tools when examining numerical relationships, and computer software which allows exploration of number relationships through conversion utilities and graphs opens up even more possibilities.

The topics that should comprise the number sense focus of the ninth through twelfth grade mathematics program are:

the real number system

exponents, roots, and scientific notation

properties of number systems

The cumulative progress indicators for grade 12 appear below in boldface type. Each indicator is followed by activities which illustrate how it can be addressed in the classroom in grades 9, 10, 11, and 12.

Building upon knowledge and skills gained in the preceding grades, experiences in grades 9-12 will be such that all students:

20. Extend their understanding of the number system to include real numbers and an awareness of other number systems.

• Students explore alternative number bases and note their advantages and disadvantages. Binary and hexadecimal systems are of primary interest because of their use in computer programming.

• Students read about and understand the historical relationship between the square root of 2 and the Pythagoreans' attempt to express the length of the diagonal of a square in terms of its sides. They use geoboards to illustrate how the hypotenuse of a right triangle can represent a length of sqrt(2), sqrt(3), or sqrt(5), and so on.

• Students' understanding of real numbers is assessed by asking them to locate rational and irrational numbers on a number line.

• Students find two numbers between any two given real numbers, such as .4222... and .424242... .

• Students can give examples of irrational numbers such as 3.010010001 ... or .4323323332 ... .

21. Develop conjectures and informal proofs of properties of number systems and sets of numbers.

• Students discuss whether the transitive and reflexive properties hold for different relationships, such as "is a friend of", "is perpendicular to," or "is a factor of."

• Students make up a number system using the symbols , , , and . They develop algorithms for adding and multiplying within their system and decide whether these operations are commutative and associative.

• Students explore the properties of clock arithmetic or a modular arithmetic system.

• Students examine properties involving addition of matrices, scalar multiplication, and matrix multiplication. They demonstrate that matrix multiplication is not commutative by providing a counter-example.

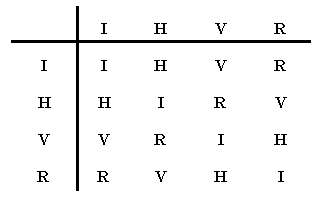
• Students investigate transformations of the rectangle ABCD: reflection about its the horizontal line of symmetry (H), reflection about its vertical line of symmetry (V), rotation by 180 degrees (R), and rotation by 360 degrees (the identity, I). They construct an operations table (see below) which tells what happens if one of these transformations is followed by another. Thus, for example, if you reflect about the vertical line of symmetry (V) and then rotate by 180 degrees (R), the result is the same as reflecting about the horizontal line of symmetry (H); this is indicated in the table by placing H as the entry in the row for V and column for R representing the conclusion that V followed by R is H. Students investigate the properties of this operation "followed by."
  

22. Extend their intuitive grasp of number relationships, uses, and interpretations and develop an ability to work with rational and irrational numbers.

• Students create computer spreadsheets to help assess real-world and purely mathematical numerical situations and to ask what if questions regarding complex data.

• Students use calculators and the formula for compound interest to answer specific questions regarding the amount of money that will be in a particular bank account after 1, 10, and 100 years.

• Students informally solve maximum/minimum problems with the help of graphing calculators.

• Students use formulas for projectile motion to solve problems regarding distance traveled, time in flight, maximum height, and so on.

• Students compare different representations for pi, including 3.14, 22/7, and the value given by their calculators. They discuss the accuracy of each approximation, suggesting appropriate circumstances for its use.

• Students work through the Ice Cones lesson that is described in the First Four Standards of this Framework. They use graphing calculations to determine the maximum volume of a cone created from a 10 inch circle which is cut along a radius.

23. Explore a variety of infinite sequences and informally evaluate their limits.

• Students explore the value of .99 ... (or 4.999... or 3.2999...) as an infinite series (9/10 + 9/100 + ... ), and conclude that its value is exactly 1 (or 5 or 3.3).

• Students analyze and discuss the sums of infinite series such as the following:
  

  1 - 1 + 1 - 1 + 1 - 1 + ...

  ( 1 - 1) + (1 - 1) + (1 - 1) + ...

  1 + (- 1 + 1) + (-1 + 1) + (-1 + 1) + ...

• Students informally find the limits of real-world series such as the total vertical distance traveled by a ball dropped from a height of 10 meters which always bounces back to 3/4 of its original height.

• Students investigate the sums of series such as:
  

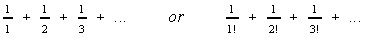
• Students estimate the area of a circle with radius of 10 by informally judging the limiting value of the sequence produced by the areas of inscribed regular polygons as their sides increase by 1; that is, they calculate the area of an inscribed equilateral triangle, an inscribed square, an inscribed pentagon, and so on.

• Students discuss pyramid schemes and create a mathematical model to determine how many people would have to participate in the scheme for everyone at the fifth level to be paid, for everyone at the tenth level to be paid, and then for everyone who participated at any level to be paid. For example, if each person pays four others, then there are 4ⁿ people at the nth level.

References

National Council of Teachers of Mathematics. Curriculum and Evaluation Standards for School Mathematics. Reston, VA, 1989.

On-Line Resources

http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/

The Framework will be available at this site during Spring 1997. In time, we hope to post additional resources relating to this standard, such as grade-specific activities submitted by New Jersey teachers, and to provide a forum to discuss the Mathematics Standards.