Students can develop strong spatial sense from consistent experiences in classroom activities that use a wide variety of manipulatives and technology. The key components of spatial sense, as identified in the K-12 Overview, are spatial relationships, properties of geometric figures, geometric transformations, coordinate geometry, geometry of measurement, geometric modeling, and reasoning.

Informal geometry and spatial visualization are vital aspects of a mathematics program for grades 5 and 6. Middle school students experience the fun and challenge of learning geometry through creating plans, building models, drawing, sorting and classifying objects, and discovering, visualizing, and representing concepts and geometric properties. Students develop the understanding needed to function in a three-dimensional world through explorations and investigations organized around physical models.

Studying geometry also provides opportunities for divergent thinking and creative problem solving while developing students' logical thinking abilities. Geometric concepts and representations can help students better understand number concepts while being particularly well-suited for addressing the First Four Standards: problem solving, reasoning, making connections, and communicating mathematics.

Students' experiences in learning geometry should help them perceive geometry as having a dynamically important role in their environment and not merely as the learning of vocabulary, memorizing definitions and formulas, and stating properties of shapes. Students, working in groups or independently, should explore and investigate problems in two and three dimensions, make and test conjectures, construct and use models, drawings, and computer technology, develop spatial sense, use inductive and deductive reasoning, and then communicate their results with confidence and conviction. They should be challenged to find alternative approaches and solutions.

In their study of spatial relationships, students in grades 5 and 6 further develop their understanding of projections (e.g., top, front, and side views), perspectives (e.g., drawings made on isometric dot paper), and maps. They also consolidate their understanding of the concepts of symmetry (both line and rotational), congruence, and similarity.

Students expand their understanding of properties of geometric figures by using models to develop the concepts needed to make abstractions and generalizations. They focus on the properties of lines and planes as well as on those of plane and solid geometric figures. Students at this age begin to classify geometric figures according to common properties and develop informal definitions.

Still using models, drawings, and computer graphics, students expand their understanding of geometric transformation, including translations (slides), reflections (flips), rotations (turns), and dilations (stretchers/shrinkers). At these grade levels, the connections between transformations and congruence, similarity, and symmetry are explored. Students also begin to use coordinate geometry to show how figures change orientation but not shape under transformations. For these investigations they use all four quadrants of the coordinate plane (positive and negative numbers).

Students develop greater understanding of the geometry of measurement as they develop strategies for finding perimeters, areas (of rectangles and triangles), volumes, surface areas, and angle measures. The emphasis at this level should be on looking for different ways to find an answer, not simply on using formulas. Students use models for many problems, look for patterns in their answers, and form conjectures about general methods that might be appropriate for certain types of problems. Students apply what they are learning about areas to help them develop an understanding of the Pythagorean Theorem.

Students continue to use geometric modeling to help them solve a variety of problems. They explore patterns of geometric change as well as those involving number patterns. They use geometric representations to assist them in solving problems in discrete mathematics. They use concrete materials, drawings, and computers to help them visualize geometric patterns.

Students in these grade levels are beginning to develop more sophisticated reasoning skills. In studying geometry, they have many opportunities to make conjectures based on data they have collected and patterns they have observed. This inductive reasoning can then be related to what they already know; students should be encouraged to explain their thinking and justify their responses.

Throughout fifth and sixth grade, students use concrete materials, drawings, and computer graphics to increase the number of geometric concepts with which they are familiar and to explore how these concepts can be used in geometric reasoning. Students' natural curiosity about the world provides ample opportunities for linking mathematics with other subjects. The continued experience with two- and three-dimensional figures provided at these grade levels helps students build the firm foundation needed for the more formal geometry of the secondary school.

The cumulative progress indicators for grade 8 appear below in boldface type. Each indicator is followed by activities which illustrate how it can be addressed in the classroom in grades 5 and 6.

Building upon knowledge and skills gained in the preceding grades, experiences in grades 5-6 will be such that all students:

11. Relate two-dimensional and three-dimensional geometry using shadows, perspectives, projections, and maps.

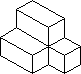
• Students use centimeter cubes to construct a building such as the one pictured below. They then represent their building by drawing the base and telling how many cubes are stacked in each portion of building.

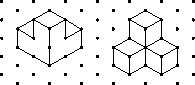
• Students put three or four cubes together to make a solid and draw two different projective views of the solid on triangle dot paper, such as those shown below.
  

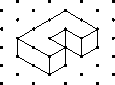
• Students copy pictures of solids drawn on triangle dot paper such as the one below, build the solids, and find their volumes.
  

• Students use circles and rectangles to make 3-dimensional models of cylinders, cones, prisms, and other solids.

• Students predict and sketch the shapes of the faces of a pyramid, or, given a flat design for a box, predict what it will look like when put together.

12. Understand and apply the concepts of symmetry, similarity, and congruence.

• Students compare different Logo procedures for drawing similar rectangles.

• Students look for examples of congruent figures (same size and shape) in the environment.

• Students explore symmetry by looking at the designs formed by placing a mirror on a pattern block design somewhere other than the line of symmetry, or by folding paper more than one time. They identify the symmetry in wallpaper or giftwrap designs. They also identify the rotational symmetry found in a pinwheel (e.g., 90 degrees). (The figure matches itself by turning rather than by flipping or folding.)

• Students build scale models to investigate similarity. They recognize that figures which have the same shape but different sizes are similar.

13. Identify, describe, compare, and classify plane and solid geometric figures.

• Students are given a sheet of 3 x 3 dot paper grids. They find and draw as many noncongruent quadrilaterals as they can, using a different set of nine dots for each figure; altogether sixteen different quadrilaterals (pictured below) can be formed.
  

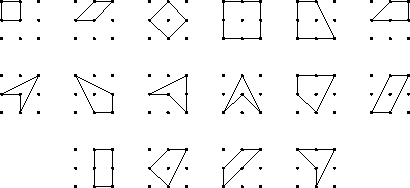
A nice open-ended approach to assessment of their understanding and comfort with properties of geometric figures is to ask them to sort these quadrilaterals in different ways, including concave vs. convex, by angle sizes, by area, by symmetry, and so on. See how many ways they can devise.

• Students trace a figure onto several transparencies; figures such as squares, rectangles, parallelograms, rhombuses, trapezoids, kites, and arrowheads can be used. Then they draw the lines of symmetry for the figure. They rotate, translate, and flip the transparencies and compare them to an original transparency to investigate such properties as: the number of congruent sides in the figure, the number of parallel sides in the figure, whether the diagonals are congruent, whether the diagonals bisect each other, whether the diagonals are perpendicular, and whether the figure has half-turn symmetry (180 degrees). They write about their findings and explain their reasoning.

• Students use Logo to investigate the sum of the measures of the exterior angles of any polygon (360 degrees) and the angle measure of each exterior angle of a regular polygon.

• Students select straws cut to five different lengths (for example, from one inch to five inches) and form as many different triangles as they can, recording the results. They sort the triangles into groups with 0, 2, or 3 equal sides and label the groups as scalene, isosceles, and equilateral triangles.

14. Understand the properties of lines and planes, including parallel and perpendicular lines and planes, and intersecting lines and planes and their angles of incidence.

• Students use index cards with slits cut in them to build models of two planes that are parallel or two planes that intersect (in a line).

• Students use toothpicks to explore how two lines might be related to each other (parallel, intersecting, perpendicular, the same line).

• Students find examples of parallel lines and planes, perpendicular lines and planes, and intersecting lines and planes with different angles in their environment.

15. Explore the relationships among geometric transformations (translations, reflections, rotations, and dilations), tessellations (tilings), and congruence and similarity.

• Students read and examine The World of M.C. Escher or any other collection of M.C. Escher's work to find and describe the tessellations in them. Transformations of tessellating polygons are then performed by the students to make their own artwork.

• Students create a design on a geoboard, sketch their design, move the pattern to a new spot by using a specified transformation, and sketch the result.

• Students investigate wallpaper, fabric, and gift wrap designs. They create a template for a unit figure which they will use to create individual border designs for their classroom. Each student presents her/his design to the class, describing the transformations used to create the design.

• Working in small groups, students tile a portion of their desktop using oak-tag copies they have cut of a shape they have created by taping together two pattern blocks. Each group presents its results. The teacher then asks the students to compare the results of the different groups and identify examples of the different transformations used.

• Students investigate how transformations affect the size, shape, and orientation of geometric figures. A reflection or flip is a mirror image. A translation or slide moves a figure a specified distance and direction along a straight line. A rotation or turn is a turning motion of a specified amount and direction about a fixed point, the center. These transformations do not change the size and shape of the original figure. However, a dilation enlarges (stretches) or reduces (shrinks) a figure, producing a new figure with the same shape but a different size.

• Students use Tesselmania! software to manipulate and transform colorful shapes on the computer screen and create complex tessellations.

• Students continue to look for and report on transformations they find in the world around them.

16. Develop, understand, and apply a variety of strategies for determining perimeter, area, surface area, angle measure, and volume.

• Students are given a transparent square grid to place over a worksheet with triangles drawn on it. Using the grid to measure, they find the base, height, and area of each triangle, recording their findings in a table. They discuss patterns that they see, developing their own formula to find areas of triangles.

• Students find the perimeter of a figure by taping a string around it and then untaping and measuring the string. For something large, like the classroom, they might construct and use a trundle wheel.

• Students first estimate the perimeter (or area, volume, or surface area) of a classroom object, then measure it, determine its perimeter, and compare their answers to their estimates. Objects which might be used include books, desks, closets, doors, or windows.

• Students use various same-shape pattern blocks and arrange as many as are needed around a point to complete a circle. They discover the size of each angle since there are 360 degrees in one circle. For example, if it takes six (green) triangles, then each angle must be 60 degrees (360 degrees ÷ 6).

• Students are given a sheet with rectilinear figures (only right angles) on it, such as the letter "E" at the right, and a transparent square centimeter grid that they can place over each of the figures. By counting the squares, they can find the area of each figure; by counting the number of units around it, they can determine its perimeter.

• Students use centimeter cubes to build a structure such as the one shown below and then count the cubes to find the volume of the structure.
  

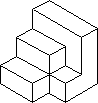
• Students bring cereal boxes from home, cut them apart, and determine their surface areas.

• Students find the volumes of different backpacks by using familiar solids to approximate their shape. They compare their results and write about which backpack they think would be "best" and why.

17. Understand and apply the Pythagorean Theorem.

• Students construct squares on each side of a right triangle on a geoboard and find the area of each square. They repeat this process using several different triangles, recording their results in a table. Then they look for patterns in the table.

• Students measure the distance diagonally from first to third base on a baseball field and compare it to the distance run by a player who goes from first to second to third. Theynote that it is a shorter distance diagonally across the field than it is along the two sides. They repeat this type of measuring activity for other squares and rectangles, noting their results in a table and discussing any patterns they see. They calculate the square of each of the three sides of each triangle, record their results in a table, and look for patterns.

18. Explore patterns produced by processes of geometric change, relating iteration, approximation, and fractals.

• Students use the reducing and/or enlarging feature on a copier to explore repeated reductions/enlargements by the same factor (iteration).

• Students investigate the natural shapes that are produced by growth. They look at how nature produces complex structures in which basic shapes occur over and over. For example, spider webs, honeycombs, pineapples, pinecones, nautilus shells, and snowflakes grow larger in a systematic way (iteration).

19. Investigate, explore, and describe the geometry in nature and real-world applications, using models, manipulatives, and appropriate technology.

• Students design a three-dimensional geometric sculpture. Some may want to find plans for making a geodesic dome and construct it out of gumdrops and toothpicks.

• Students work through the Two-Toned Towers lesson that is described in the First Four Standards of this Framework. They use models to determine how many different towers can be built using four blocks of two different colors.

• Groups of students working together design a doghouse to be built from a 4' x 8' sheet of plywood. They construct a scale model of their design from oaktag.

• Students use computer programs like The Geometry PreSupposer to explore the relationships of sides of polygons or properties of quadrilaterals.

• Assessments that make use of manipulatives and computer software allow students to demonstrate their knowledge and understanding of geometry. The results of performance tasks such as the following would be appropriate for a portfolio: Make as many different sized squares as you can on a fivebyfive geoboard. Create a tessellation pattern with pattern blocks or Tessellmania! software that uses slides, flips, and turns.

• Students select a country or culture, research the use of specific geometric patterns in that culture, and make a report to the class.

• Specific manipulatives that may be helpful for geometry include pattern blocks, color tiles, linking cubes, centimeter cubes, tangrams, geoboards, links, and templates. Computer programs such as Logo, Shape Up!, Elastic Lines, Building Perspective, or The Factory may also be helpful.

References

Looher, J. L, Ed. The World of M. C. Escher. New York: Abradale Press, Harry N. Abrams, Inc., 1971, 1988.

Software

Building Perspective. Sunburst Communications.

Elastic Lines. Sunburst Communications.

Logo. Many versions of Logo are commercially available.

Shape Up! Sunburst Communications.

Tesselmania! Minnesota Educational Computing Consortium (MECC).

The Factory. Sunburst Communications.

The Geometry PreSupposer. Sunburst Communications.

General references

Diggins, Julia. String, Straightedge, and Shadow: The Story of Geometry. New York: Viking Press, 1965.

Geddes, D. Curriculum and Evaluation Standards for School Mathematics: Addenda Series: Geometry in the Middle Grades. Reston, VA: National Council of Teachers of Mathematics, 1992.

On-Line Resources

http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/

The Framework will be available at this site during Spring 1997. In time, we hope to post additional resources relating to this standard, such as grade-specific activities submitted by New Jersey teachers, and to provide a forum to discuss the Mathematics Standards.