STANDARD 7 - GEOMETRY AND SPATIAL SENSE
|
All students will develop spatial sense and an ability to use
geometric properties and relationships to solve problems in
mathematics and in everyday life.
|
Standard 7 - Geometry and Spatial Sense - Grades 9-12
Overview
Students can develop a strong spatial sense from consistent
experiences in classroom activities which use a wide variety of
manipulatives and technology. The key components of this spatial
sense, as identified in the K-12 Overview, are spatial relationships,
properties of geometric figures, geometric transformations, coordinate
geometry, geometry of measurement, geometric modeling, and
reasoning.
Geometry has historically held an important role in high school
mathematics, primarily through its focus on deductive reasoning and
proof; developing skills in deductive reasoning, learning how to
construct proofs, and understanding geometric properties are important
outcomes of the high school geometry course. Equally important,
however, is the continued development of visualization skills,
pictorial representations, and applications of geometric ideas since
geometry helps students represent and describe the world in which they
live and answer questions about natural, physical, and social
phenomena.
Deductive reasoning is highly dependent upon understanding and
communication skills. In fact, mathematics can be considered as a
language - a language of patterns. This language of mathematics
must be meaningful if students are to discuss mathematics, construct
arguments, and apply geometry productively. Communication and
language play a critical role in helping students to construct links
between their informal, intuitive geometric notions and the more
abstract language and symbolism of high school geometry.
Geometry describes the real world from several viewpoints. One
viewpoint is that of standard Euclidean geometry - a deductive
system developed from basic axioms. Other widely used viewpoints are
those of coordinate geometry, transformational geometry, and vector
geometry. The interplay between geometry and algebra strengthens the
students' ability to formulate and analyze problems from
situations both within and outside mathematics. Although students
will at times work separately in synthetic, coordinate,
transformational, and vector geometry, they should also have many
opportunities to compare, contrast, and translate among these systems.
Further, students should learn that certain types of problems are
often solved more easily in one specific system than another specific
system.
Visualization and pictorial representation are also important
aspects of a high school geometry course. Students should have
opportunities to visualize and work with two- and three-dimensional
figures in order to develop spatial skills fundamental to everyday
life and to many careers. By using physical models and other
real-world objects, students can develop a strong base for geometric
intuition. They can then draw upon these experiences and intuitions
when working with abstract ideas.
The goal of high school geometry includes applying geometric ideas
to problems in a variety of areas. Each student must develop the
ability to solve problems if he or she is to become a productive
citizen. Instruction thus must begin with problem situations -
not only exercises to be accomplished independently but also problems
to be solved in small groups or by the entire class working
cooperatively.
Applications of mathematics have changed dramatically over the last
twenty years, primarily due to rapid advances in technology. Geometry
has, in fact, become more important to students because of
computergraphics. Thus, calculators and computers are appropriate and
necessary tools in learning geometry.
Students in high school continue to develop their understanding of
spatial relationships. They construct models from
two-dimensional representations of objects, they interpret two- and
three-dimensional representations of geometric objects, and they
construct two-dimensional representations of actual objects.
Students formalize their understanding of properties of
geometric figures, using known properties to deduce new
relationships. Specific figures which are studied include polygons,
circles, prisms, cylinders, pyramids, cones, and spheres. Properties
considered should include congruence, similarity, symmetry, measures
of angles (especially special relationships such as supplementary and
complementary angles), parallelism, and perpendicularity.
In high school, students apply the principles of geometric
transformations and coordinate geometry that they learned
in the earlier grades, using these to help develop further
understanding of geometric concepts and to establish justifications
for conclusions inferred about geometric objects and their
relationships. They also begin to use vectors to represent geometric
situations.
The geometry of measurement is extended in the high school
grades to include formalizing procedures for finding perimeters,
circumferences, areas, volumes, and surface areas, and solving
indirect measurement problems using trigonometric ratios. Students
should also use trigonometric functions to model periodic phenomena,
establishing an important connection between geometry and algebra.
Students use a variety of geometric representations in geometric
modeling at these grade levels, such as graphs of algebraic
functions on coordinate grids, networks composed of vertices and
edges, vectors, transformations, and right triangles to solve problems
involving trigonometry. They also explore and analyze further the
patterns produced by geometric change.
Deductive reasoning takes on an increasingly important role
in the high school years. Students use inductive reasoning as they
look for patterns and make conjectures; they use deductive reasoning
to justify their conjectures and present reasonable explanations.
Standard 7 - Geometry and Spatial Sense - Grades 9-12
Indicators and Activities
The cumulative progress indicators for grade 12 appear below in
boldface type. Each indicator is followed by activities which
illustrate how it can be addressed in the classroom in grades 9, 10,
11 and 12.
Building upon knowledge and skills gained in the preceding grades,
experiences in grades 9-12 will be such that all students:
16*. Develop, understand, and apply a
variety of strategies for determining perimeter, area, surface
area, angle measure, and volume.
- Students find volumes of objects formed by
combining geometric figures and develop formulas describing what they
have done. For example, they might generate a formula for finding the
volume of a silo composed of a cylinder of specified radius and height
topped by a hemisphere of the same radius.
- Students construct models to show how the volume
of a pyramid with a square base and height equal to a side of the base
is related to the volume of a cube with the same base.
- Students develop and use a spreadsheet to
determine what the dimensions should be for a cylinder with a fixed
volume, in order to minimize the surface area. Similarly, they
investigate what should be the dimensions for a rectangle having a
fixed perimeter in order to maximize the enclosed area. They discuss
how the symmetry of these figures relates to the
solutions.
19*. Investigate, explore, and
describe geometry in nature and real-world applications, using
models, manipulatives, and appropriate technology.
- Students use a computer-aided design (CAD)
program to investigate rotations of objects in three
dimensions.
- Students use The Geometric SuperSupposer
to measure components of shapes and make observations. For example,
they might construct parallelograms and measure sides, angles, and
diagonals, observing that opposite sides are congruent, as are
opposite angles, and that diagonals bisect each other.
- Students use The Geometer's
Sketchpad to investigate the effects of rotating a triangle about
a fixed point.
- Students use commercial materials such as
GeoShapes or Polydrons to construct three-dimensional geometric
figures. They make tables concerning the number of vertices, edges,
and faces in each solid. They measure the figures to determine their
surface areas and volumes. They lay the patterns out flat to examine
the nets of each solid. [A net is aflat shape which when folded along
indicated lines will produce a three-dimensional object; for example,
six identical squares joined in the shape of a cross can be folded to
form a cube. Tabs added to the net facilitate attaching appropriate
edges so that the shape remains three-dimensional.]
- Students work through the Ice Cones
lesson that is described in the First Four Standards of this
Framework. Students create a variety of paper cones out of
circles with radius 10 inches which are cut along a radius. They use
graphing calculators to find the maximum volume of such
cones.
- Students copy geometric designs using compass
and straightedge, and generate their own designs.
- Students investigate wallpaper patterns,
classifying them according to the transformations used. They study
the structure of crystals from a geometric perspective.
20. Understand and apply properties involving angles,
parallel lines, and perpendicular lines.
- Students make tessellations with an assortment of different
triangles, noting the variety of geometric patterns that are formed,
including parallel lines, congruent angles, congruent triangles,
similar triangles, parallelograms, and trapezoids.
- Students identify congruent angles on a parallelogram grid,
and use their results to develop conjectures about alternate interior
angles, corresponding angles of parallel lines, and opposite angles of
a parallelogram.
- Working together, students review geometric vocabulary by
sorting words written on index cards into groups and explaining their
reasons for creating the groups they did. For example, they might
place "parallelogram," "rhombus,"
"square," and "rectangle" in one group (since they
are all parallelograms) and place "kite" and
"trapezoid" in another group (since they are not
parallelograms).
- Students find a variety of strategies for
demonstrating that the sum of the measures of the angles of a triangle
is 180 degrees. Some use protractors and measure a pencil-and-paper
figure, others create a triangle with Geometer's
Sketchpad software and post the measures of the angles before
dragging it from a vertex to notice that the sum always remains the
same, and still others use a method that requires tearing each of the
corners from an oaktag triangle and then fitting them together to make
a line.
21. Analyze properties of three-dimensional shapes by
constructing models and by drawing and interpreting
two-dimensional representations of them.
- Pairs of students work together to describe and draw
geometric figures. One student is given a picture involving one or
more geometric figures and must describe the drawing to the other
student without using the names of the figures. The second student,
without seeing the figure, must visualize and represent the
picture.
- Students create wind-up posterboard models of rotational
three-dimensional solids. They cut out a plane figure such as a
circle or a rectangle from posterboard, punch two holes in it near its
edges, thread a cut rubberband through the holes, and attach the ends
of the rubberband to the ends of a coathanger from which the
horizontal wire has been removed. They then twist the rubber band to
wind up the figure and release to "show" the solid.
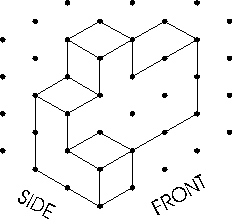
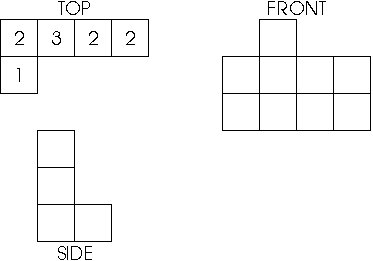
- Students use isometric dot paper to sketch figures made up
of cubes. They also sketch top, front, and side views (projections)
of the figure.
- One long-term project that some high school
teachers use for assessment is the following: Using a variety of means
and materials, students begin by constructing models of the Platonic
solids and other three dimensional geometric figures. They are then
challenged to work in teams to find a relationship among the number of
faces, vertices, and edges that holds for all of the solids
(Euler's Formula: F + V - E = 2).
- Students read Flatland: A Romance of Many
Dimensions by Edwin Abbott, a fascinating and imaginative story
about life in a two-dimensional world.
- Students use a computer-aided design (CAD)
program to investigate rotations of objects in three
dimensions.
22. Use transformations, coordinates, and vectors to
solve problems in Euclidean geometry.
- Students construct a polygon that outlines the top view of
their school. They are asked to imagine that they are architects who
need to send this outline by computer to a builder who has no graphics
imaging capabilities. They develop strategies for sending this
information to the builder. One group locates one corner of the
building at the origin and determines the coordinates for the other
vertices. Another group uses vectors to tell the builder what
direction to proceed from the initial corner located at the
origin.
- Students work on the question of where a power transformer
should be located on a line so that the length of the cable needed to
run to two points not on that line is minimized. They find that if
the two points are on the same side of the line, then by using
reflections they can construct a straight line that crosses the given
line at the desired location.
- Students first determine the coordinates for the vertices
of a parallelogram, a rhombus, a rectangle, an isosceles trapezoid,
and a square with one vertex at the origin and a side along the
x-axis. They then work in groups to determine where the coordinate
system should be placed to simplify the coordinate selection for a
kite, a rhombus, and a square.
- Students draw two congruent triangles anywhere in the plane
and determine the minimum number of reflections needed to map one onto
the other.
- Students draw a triangle on graph paper and then find the
image of the triangle when the coordinates of each vertex are
multiplied by various constants. They draw each resulting triangle
and determine its area. They make a table of their results and look
for relationships between the constants used for dilation and the
ratios of the areas.
- Students use a Mira (Reflecta) to find the center of a
circle, to draw the perpendicular bisectors of a line segment, or to
draw the medians of a triangle.
- Students apply transformations to figures drawn on
coordinate grids, record the coordinates of the original figure and
its image, and look for patterns. They express these patterns
verbally and symbolically. For example, flipping a point across the
x-axis changes the sign of the y-coordinate so that the point (x,y)
moves to (x, -y).
- Given the equation of a line, students plot the
line on a coordinate grid and then shift the line according to a given
translation. They then determine the equation of the resulting line.
After doing several such problems, students identify patterns that
they have found and write conjectures.
- Students work through the Building
Parabolas lesson that is described in the First Four Standards of
this Framework. They investigate the effects of various
coefficients on the general shape of a parabola and connect these to
geometric transformations.
23. Use basic trigonometric ratios to solve problems
involving indirect measurement.
- Students use trigonometric ratios to determine distances
which cannot be measured directly, such as the distance between two
points on opposite sides of a chasm.
- Students investigate how the paths of tunnels are
determined so that people digging from each end wind up in the same
place.
- Students use trigonometry to determine the cloud ceiling at
night by directing a light (kept in a narrow beam by a parabolic
reflector) toward the clouds. An observer at a specified distance
measures the angle of elevation to the point at which the light is
reflected from the cloud.
- Students plot the average high temperature for each month
over the course of five years to see an example of a periodic
function. They discuss what types of functions might be appropriate
to represent this relationship.
24. Solve real-world and mathematical problems using
geometric models.
- Students visit a construction site where the
"framing" step of a building process is taking place. They
note where congruence occurs (such as in the beams of the roof, where
angles must be congruent). They write about why congruence is
essential to buildings and other structures.
- Students use paper fasteners and tagboard strips with a
hole punched near each end to investigate the rigidity of various
polygon shapes. For shapes that are not rigid, they determine how to
make the shape more rigid.
- Students draw a geometric
representation and develop a formula to solve the problem of how many
handshakes will take place if there are n people and each
person shakes hands with each other person exactly once.
- Students work through the On the
Boardwalk lesson that is described in the Introduction to this
Framework. They determined the probability of winning a prize
when tossing a coin onto a grid by having the coin avoid all of the
grid lines.
- Students use graph models to represent a situation in which
a large company wishes to install a pneumatic tube system that would
enable small items to be sent between any of ten locales, possibly by
relay. Given the cost associated with possible tubes (edges), the
students work in groups to determine optimal pneumatic tube systems
for the company. They report their results in letters written
individually to the company president.
- Students work through the Making
Rectangles lesson that is described in the First Four Standards of
this Framework. They use combinations of algebra tiles which
they try to arrange into rectangle shapes to help them develop
procedures for multiplying binomials and factoring
polynomials.
25. Use inductive and deductive reasoning to solve
problems and to present reasonable explanations of and
justifications for the solutions.
- In a computer-based, open-ended, assessment, groups of
students use computer software to draw parallelograms, make
measurements, and list as many properties of parallelograms and their
diagonals as they can.
- Students prove deductively that a parallelogram
is divided into congruent triangle by a diagonal. They also prove
that any angle inscribed in a semi-circle is a right angle. (An angle
ABC is inscribed in a semi-circle if AC is a diameter and B is any
other point on the circle.)
- Students explain in writing to a friend what the formula is
for the measure of each interior angle in a regular polygon with
n sides and how it is derived.
- Students build staircases from cubes, recording the number
of steps and the total number of cubes used for each construction.
They look for patterns, expressing them in words and symbolically in
equations. They then try to justify their results using deductive
reasoning.
- Students use Cabri software to investigate what
happens when consecutive midpoints of a quadrilateral are connected in
order. They state a conjecture based on their investigation and
explain why they think it is true.
- Students investigate the relationship between the number
of diagonals that can be drawn from one vertex of a polygon and the
number of sides of that polygon. They write about their findings in
their journals.
- Students work through the A Sure Thing!?
lesson in the Introduction to this Framework. They investigate
the number of non-overlapping regions that can be created if they draw
all the chords joining n points on the circumference of a
circle.
26. Analyze patterns produced by processes of
geometric change and express them in terms of iteration,
approximation, limits, self-similarity, and fractals.
- Students duplicate the beginning stages of a fractal
construction in the plane and analyze the sequences of their
perimeters and their areas.
- Students use the reduction and enlargement capabilities of
a copy machine to investigate the effects on area. They make a table
showing the linear rate of reduction/enlargement and the resulting
area for each successive reduction/enlargement. Then they graph the
results - an exponential function showing either decay or
growth.
- Students use the slides and appropriate
activities from Fractals for the Classroom, Vol. 1 to analyze
patterns produced by changes in geometric shapes.
- Students model decay in a bacterial culture by cutting a
sheet of grid paper in half repeatedly and recording the area of each
rectangle in a table. They then graph the number of cuts versus the
area to see an example of exponential decay.
- Students plot the relationship between body height and arm
length for people from one year of age through adulthood on coordinate
grid paper and on log-log paper. They see that the graph is not a
straight line on the coordinate grid paper; it is actually a
logarithmic function. They find that the function appears as a
straight line on log-log paper.
27. Explore applications of other geometries in
real-world contexts.
|