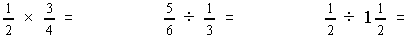Estimation, as described in the K-12 Overview includes three primary themes: determining the reasonableness of answers, using a variety of estimation strategies in a variety of situations, and estimating the results of computations.

In seventh and eighth grade, estimation and number sense are much more important skills than algorithmic paper-and-pencil computation with whole numbers. Students should become masters at applying estimation strategies so that an answer displayed on a calculator is instinctively compared to a reasonable range in which the correct answer lies. It is critical that students understand the displays that occur on the screen and the effects of calculator rounding either because of the calculator's own operational system or because of user-defined constraints. Issues of the number of significant figures and what kinds of answers make sense in a given problem setting create new reasons to focus on reasonableness of answers.

The new estimation skills begun in fifth and sixth grade are still being developed in the seventh and eighth grades. These include skills in estimating the results of fraction and decimal computations. As students deepen their understanding of these numbers and perform operations with them, estimation ought always to be present. Estimation of quantities in fraction or decimal terms as a result of operations on those numbers is just as important for the mathematically literate adult as the same skills with whole numbers.

In addition, the seventh and eighth grades present students with opportunities to develop strategies for estimation with ratios, proportions, and percents. Estimation and number sense must play an important role in the lessons dealing with these concepts so that students feel comfortable with the relative effects of operations on them. Another new opportunity here is estimation of roots. It should be well within every eighth grader's ability, for example, to estimate the square root of 40.

Students should understand that sometimes, an estimate will be accurate enough to serve as an answer. At other times, an exact computation will need to be done, either mentally, with paper-and-pencil, or with a calculator. Even in cases where exact answers are to be calculated, however, students must understand that it is almost always a good idea to have an estimate in mind so that the computed answer can be checked against it.

The cumulative progress indicators for grade 8 appear below in boldface type. Each indicator is followed by activities which illustrate how it can be addressed in the classroom in grades 7 and 8.

Building upon knowledge and skills gained in the preceding grades, experiences in grades 7-8 will be such that all students:

5^*. Recognize when estimation is appropriate, and understand the usefulness of an estimate as distinct from an exact answer.

• Students regularly tackle problems for which estimation is the only possible approach. For example: How many hairs are on your head? or How many grains of rice are in this ten-pound bag? Solution strategies are always discussed with the whole class.

• Students create a plan to "win a contract" by bidding on projects. For example: Your class has been given one day to sell peanuts at Shea Stadium. Prepare a presentation that includes the amount of peanuts to order, the costs of selling the peanuts, the profits that will be made, and the other logistics of selling the peanuts. Organize a schedule with estimated times for completion for the entire project.

• Students use estimation skills to run a business using Hot Dog Stand or Survival Math software.

• Students apply estimation skills to algebraic situation as they try to guess the equations to hit the most globs in Green Globs software.

6. Determine the reasonableness of an answer by estimating the result of operations.

• Students estimate whether or not they can buy a set of items with a given amount of money. For example: I have only $50. Can I buy a reel, a rod, and a tackle box during the sale advertised below?

ALL ITEMS 1/3 OFF AT JAKE'S FISHING WORLD!

ITEM		REGULAR PRICE
Daiwa Reels		$29.95 each
Ugly Stick Rods		$20.00 each
Tackle Boxes		$17.99 each

To assess students' performance, the teacher asks them to write about how they can answer this question without doing any exact computations.

If 6% sales tax is charged, can you tell whether $50 is enough by estimating? Explain. Calculate the exact price including tax.

• Students evaluate various statements made by public figures to decide whether they are reasonable. For example: The Phillies' center fielder announced that he expected to get 225 hits this season. Do you think he will? In order to determine what confidence to have in that prediction, a variety of factors need to be estimated: number of at-bats, lifetime batting average, likelihood of injury, whether a baseball strike will occur, and so on.

• Students discuss events in their lives that might have the following likelihoods of occurring:

  100%, 0.5 %, 3/4, 95%

• Students simulate estimating the number of fish in a lake by estimating the number of fish crackers in a box using the following method. Some of the fish are removed from the box and "tagged" by marking them with food coloring. They are "released" to "swim" as they are mixed in with the other crackers in the box. Another sample is drawn and the number of tagged fish and the total number of fish are recorded. This data is used to set up a proportion (# tagged initially: total # fish = # tagged caught: total # caught) to predict the total number of fish in the box. The estimate is further improved by taking additional samples, making predictions based on each sample of the total number of fish in the box, and finally averaging all the predictions.

8. Develop, apply, and explain a variety of different estimation strategies in problem situations involving quantities and measurement.

• Students regularly have opportunities to estimate answers to straight-forward computation problems and to discuss the strategies they use in making the estimations. Even relatively routine problems generate interesting discussions and a greater shared number sense within the class:

  23% of 123, 5 x 38, 28 x 425, 486 x 2004, 423÷71

• Given a ream of paper, students work in small groups to estimate the thickness of one sheet of paper. Answers and strategies are compared across groups and explanations for differences in the estimates are sought. To assess student understanding, the teacher asks each student to write about how his or her group solved the problem.

• Students develop strategies for estimating the results of operations on fractions as they work with them. For example, a seventh grade class is asked to determine which of these computation problems have answers greater than 1 without actually performing the calculation:
  

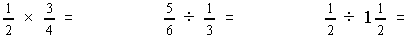
• Students make estimates of the number of answering machines, cellular phones, and fax machines in the United States and check their results against data from America by the Numbers by Les Krantz.

• Students estimate the total number of people attending National Football League games by determining how many teams there are, how many games each plays, and what the average attendance at a game might be. They then use these estimates to determine theoverall answer (17,024,000 according to America by the Numbers, p. 194).

• Students determine the amount of paper thrown away at their school each week (or month or year) by collecting the paper thrown away in their math class for one day and multiplying this by the number of classes in the school and then by five (or 30 or 50).

9. Use equivalent representations of numbers such as fractions, decimals, and percents to facilitate estimation.

• Students use fractions, decimals, or mixed numbers interchangeably when one form of the number makes estimation easier than another. For example, rather than estimating 33_% of $120, students consider 1/3 x 120 which yields a much quicker estimate.

• Similarly, in their work with percents, students master the common fraction equivalents for familiar percentages and use fractions for estimation in appropriate situations. For example, an estimate of 117% of 50 can most easily be obtained by considering 6/5 of 50.

• Students collect and bring to class sales circulars from local papers which express the discounts on sale items in a variety of ways including percent off, fraction off, and dollar amount off. For items chosen from the circular, the students discuss which form is the easiest form of expression of the discount, which is most understandable to the consumer, and which makes the sale seem the biggest bargain.

10. Determine whether a given estimate is an overestimate or an underestimate.

• Using calculators, but without using the square root key, students try to find good approximations for a few square roots, for example, the square root of 40. Through a series of approximations, they make a guess, perform the multiplication on the calculator, determine whether the approximation was too large or too small, adjust it, and begin again. This series of approximations, in itself a very useful strategy, continues until an approximation is reached that is satisfactory.

• Students compare three different rounding strategies:

  Round everything up: for example, 2345, rounded to the nearest ten, would be 2350. To the nearest hundred, it would be 2400.

  Round up if 5 or more, down if less than 5: for example, 2345, rounded to the nearest ten, would be 2350. To the nearest hundred, it would be 2300.

  Round up if more than 5, down if less than 5; and for the special case when the digit equals five make the preceding digit even. That is, if the number before the five is odd, round up; if it is even, round down. For example, 2345, rounded to the nearest ten, would be 2340. To the nearest hundred, it would be 2300.

  They discuss whether each strategy would be more likely to yield an overestimate or an underestimate when adding up a total and then apply all these strategies to several situations.

References

Krantz, Les. America by the Numbers. New York: Houghton Mifflin, 1993. (Note: Some of the entries in this book are unsuitable for seventh- and eighth-graders.)

Software

Green Globs and Graphing Equations. Sunburst Communications.

Hot Dog Stand. Sunburst Communications.

Survival Math. Sunburst Communications.

On-Line Resources

http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/

The Framework will be available at this site during Spring 1997. In time, we hope to post additional resources relating to this standard, such as grade-specific activities submitted by New Jersey teachers, and to provide a forum to discuss the Mathematics Standards.