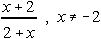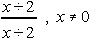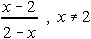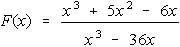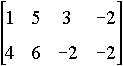STANDARD 13 - ALGEBRA
|
All students will develop an understanding of algebraic concepts
and processes and will use them to represent and analyze relationships
among variable quantities and to solve problems.
|
Standard 13 - Algebra - Grades 9-12
Overview
Students can develop a strong understanding of algebraic concepts
and processes from consistent experiences in classroom activities
where a variety of manipulatives and technology are used. The key
components of this understanding in algebra, as identified in the K-12
Overview, are: patterns, unknown quantities, properties,
functions, modeling real-world situations, evaluating expressions,
and solving equations and inequalities.
With the foundation developed in the K8 program, students should be
able to be successful in most secondary algebra programs. However,
instructional strategies should continue to focus on algebra as a
means for representing and modeling real situations and
answering questions about them. The traditional methods of teaching
algebra have been likened to teaching a foreign language, focusing on
grammar and not using the language in real conversation. Algebra
courses and programs must encourage students to "speak the
language" as well as use "proper grammar."
Algebraic understanding is necessary for all students regardless of
the structure of the 912 program. Students in mathematics programs
from technical/basic through college preparatory programs should learn
a common core of algebra, with the remainder of the program based on
their particular needs. All students should learn the same basic
ideas. All students benefit from instructional methods which provide
context for the content. Such an approach makes algebra more
understandable and motivating.
Techniques for manipulating algebraic expressions remain important,
especially for students who may continue into a calculus program.
These can be woven into the curriculum or they might all be combined
into separate courses labeled "algebra" taken by students
who intend to pursue a mathematicsrelated career. No matter how this
instruction is organized, however, instruction must produce students
who understand the logic and purposes of algebraic procedures.
Students should be comfortable with evaluating expressions
and with solving equations and inequalities, by whatever means
they find most appropriate. They should understand the relationship
between the graphs of functions and their equations. Prior to high
school, they have focused predominantly on linear functions. In high
school, students should gain more familiarity with nonlinear
functions. They should develop the ability to solve equations and
inequalities using appropriate paperandpencil techniques as well as
technology. For example, they should be able to understand and solve
quadratic equations using factoring, the quadratic formula, and
graphing, as well as with a graphing calculator. They should
recognize that the methods they use can be generalized to be used when
functions look different but are actually composite functions using a
basic type (e.g., sin2 x + 3 sin x + 2 = 0
is like x2 + 3x + 2 = 0); this
method is sometimes called "chunking." This use of
patterns to note commonalities among seemingly different
problems is an important part of algebra in the high school.
Algebraic instruction at the secondary level should provide the
opportunity for students to revisit problems. Traditional school
problems leave students with the impression that there is one right
answer and that once an answer is found there is no need to continue
to think about the problem. Since algebra is the language of
generalization, instruction in this area should encourage students to
ask questions such as Why does the solution behave this way?
They should develop an appreciation of the way algebraic
representation canmake problems easier to understand. Algebraic
instruction should be rich in problems which are meaningful to
students.
Algebra is the gatekeeper for the future study of mathematics and
of science, social sciences, business, and a host of other areas. In
the past, algebra has served as a filter, screening people out of
these opportunities. For New Jersey to be part of a global society,
it is important that 912 instruction in algebra play a major role in
the culminating experiences of a twelveyear program that opens these
gates for all.
Standard 13 - Algebra - Grades 9-12
Indicators and Activities
The cumulative progress indicators for grade 12 appear below in
boldface type. Each indicator is followed by activities which
illustrate how it can be addressed in the classroom in grades 9, 10,
11, and 12.
Building upon knowledge and skills gained in the preceding grades,
experiences in grades 9-12 will be such that all students:
14. Model and solve problems that involve varying
quantities using variables, expressions, equations,
inequalities, absolute values, vectors, and matrices.
- Students take data involving two variables in an area of
interest to them from the World Almanac, construct a scatterplot, and
predict the type of equation or function which would best model the
data. They use a computerized statistics package or a calculator to
fit a function of this type to the data. They choose from linear,
quadratic, exponential or logarithmic methods and discuss how well the
model fits as well as the limitations.
- Students use matrices to represent tabular information such
as the print runs below for each of two presses owned by a book
company. They then calculate a third matrix that indicates the growth
in production of each press from 1987 to 1988 and discuss the meaning
of the data contained in it.
| 1988 |
Textbooks |
Novels |
Nonfiction |
| Press 1 |
250,000 |
125,000 |
312,000 |
| Press 2 |
60,000 |
48,000 |
90,000 |
| 1987 |
Textbooks |
Novels |
Nonfiction |
| Press 1 |
190,000 |
100,000 |
140,000 |
| Press 2 |
45,000 |
60,000 |
72,000 |
Some students perform the operations by hand while others explain
how they would do it and then use their graphing calculator or a
spreadsheet, or write a computer program, which accomplishes the
task.
- Students use vectors to determine the path of a plane that
was flying due north at 300 miles per hour while a wind was blowing
from the southwest at a speed of 15 miles per hour. Students draw a
diagram and use an algebraic approach.
- Students work in groups on the following HSPT-like
problem from the Mathematics Instructional Guide
published by the New Jersey State Department of Education:
As you ride home from a football game, the number of kilometers
you are away from home depends (largely) on the number of
minutes you have been riding. Suppose that you are 13 km from
home when you have been riding for 10 minutes, and 8 km from home when
you have been riding for 15 minutes. (Assume that the distance
varies linearly with time.) Make a graph with the vertical axis
representing distance home and the horizontal axis representing
time. Label your graph. Plot the data given as two points on your
graph. About how long did it take (on average) to travel 1
km? About how far was the football game from your home?
Explain your answer.
- Students work through the Breaking the Mold lesson
that is described in the Introduction to this Framework. They
use a science experiment involving growing a mold to learn about
exponential growth of populations and compound interest.
- Students work through the What's My
Line unit that is described in the Keys to Success chapter of this
Framework. In this unit, students find a linear relationship
between the length of a person's thigh bone and his height, and
use this to estimate the height of a person whose thigh bone has been
found.
- Students work through the Ice Cones lesson that is
described in the First Four Standards of this Framework. In
this lesson, an ice-cream vendor's problem of folding a circle
into a cone of maximum volume is solved by expressing the volume as a
function which is then displayed on an graphing calculator.
15. Use tables and graphs as tools to
interpret expressions, equations, and inequalities.
- On a test, students are asked to determine the truth
value of the statement "log x > 0 for all positive real
numbers x." One student remembers that log x is the exponent to
which 10 must be raised to get x, and to get a number less than 1
would require a negative exponent. Another student picks some trial
points, develops a chart of the points and their logarithms and
discovers that when x < 1, log x < 0. A third student graphs
the function on his graphing calculator and sees that when x < 1,
the graph of log x is below the xaxis.
- Faced with the problem of solving the inequality
x2 3x < 4, some students use the equation
x2 3x 4 = 0 to determine the boundary points of the
interval that satisfies the inequality. They factor the equation and
find that these endpoints are 1 and 4. They place dots on the number
line at those points, since they know the endpoints are included in
the solution set, and then substitute 0 for x in the original
inequality. When they find that the resulting statement is true, they
shade the interval connecting the two points to obtain their solution
-1 < x < 4. Some students determine the endpoints in the
same way but roughly sketch a graph of the parabola y =x2
- 3 x - 4 and determine that since the inequality was < , the
problem was asking when the parabola was below the xaxis. Their graph
indicates that this happens in the region between the two endpoints.
Other students used their graphing calculators to graph the function
x2 3x and used the trace function to determine when the
graph was on or below the line y=4. All students, however, are able
to use all these methods to solve the problem.
16. Develop, explain, use, and analyze procedures for
operating on algebraic expressions and matrices.
- Students use algebra tiles to develop procedures for
multiplying binomials and factoring trinomials. They summarize these
procedures in their math notebooks, applying them to the solution of
real-world problems. They work through the Making Rectangles
lesson described in the First Four Standards of this Framework,
where they discuss which combinations of tiles can be formed into
rectangles, and relate this question to factoring trinomials.
- Students work in groups on the following
HSPT-like problem from the Mathematics Instructional
Guide (p. 7-153) published by the New Jersey State Department of
Education:
Which of the following is NOT another name for 1?
- After many experiences with trying to determine appropriate
windows for graphing functions on computers or graphing calculators,
students develop an understanding of the need to know what the general
behavior of a function will be before they use the technology.
Students are then asked to explain how they could determine the
behavior of the graph of the function below.
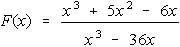
Students factor the numerator and denominator to determine the
values which make them zero and use those values to identify the
xintercepts and vertical asymptotes, respectively. They discuss the
fact that the factors x and x+6 appear in both
places and lead to a removable discontinuity represented by a hole in
the graph. They discuss the end behavior of the function as
approaching y = 1 and the behavior near the vertical
asymptote of x = 6.
- Following a unit on combinations and binomial expansion,
students make a journal entry discussing the power of Pascal's
triangle in expanding powers of binomial expressions as compared to
the traditional multiplication algorithm.
17. Solve equations and inequalities of varying
degrees using graphing calculators and computers as well as
appropriate paperandpencil techniques.
- Students are asked to find the solutions to 2x =
3x2. Some students use a spreadsheet to develop a table of
values. Once they find an interval of length 1 which contains a
solution, they refine their numbers to develop the answer to the
desired precision. Otherstudents graph both y = 2x and
y = 3x2 using graphing calculators or computers and use
the trace function to determine where they intersect. Other students
graph the function y = 3 x2 - 2x and use
the trace function to find the zeroes. Other students enter the
function in their graphing calculator and check the table of
values.
- As a portion of a final assessment, students are given one
opportunity to place a cup which is supported 6 inches off the ground
in such a position as to catch a marble rolled down a ramp. They
perform the roll without the cup to locate the point where the marble
strikes the ground. They measure the height of the end of the ramp
above the ground and the distance from the point on the ground
directly beneath the end of the ramp to the point where the marble
struck the ground. They generate the quadratic function which models
the path of the marble. Several students use different methods to
ensure they have the correct function. Then they decide where they
will have to place the cup by substituting 6 for the function value
and determining the corresponding xvalue. Students solve the equation
using the quadratic formula, and the trace function on a graphing
calculator, and proceed to place the cup and roll the ball only when
the solutions produced by all of the methods agree.
18. Understand the logic and purposes of algebraic
procedures.
- Students use matrices as arrays of information, so that
the matrix below, for example, is recognized as representing the four
vertices {(1,4), (5,6), (3, - 2), (- 2, - 2)} of a
polygon. Reducing the polygon by 1/2 can then be represented by
multiplying the matrix by the scalar 1/2 and moving the polygon to
the right one unit can be represented by adding to it a 2 x 4 matrix
whose top row consists of 1s and its bottom row of 0s.
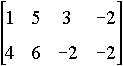
- Students read Mathematics in the Time of the
Pharaohs by Richard Gillings to understand the development of
Egyptian mathematics including computational procedures for dealing
with direct and inverse proportions, linear equations, and
trigonometric functions.
- Students explain in their journals how the identity matrix
is like the number one.
19. Interpret algebraic equations and inequalities
geometrically, and describe geometric objects
algebraically.
References
-
Gillings, Richard. Mathematics in the Time of the
Pharoahs.
New Jersey State Department of Education. Mathematics
Instructional Guide. D. Varygiannes, Coord. Trenton:
1996.
Software
-
Green Globs and Graphing Equations.
Sunburst Communications.
On-Line Resources
-
http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/
The Framework will be available at this site during Spring
1997. In time, we hope to post additional resources relating to this
standard, such as grade-specific activities submitted by New Jersey
teachers, and to provide a forum to discuss the Mathematics
Standards.
|