STANDARD 13 - ALGEBRA
|
All students will develop an understanding of algebraic concepts
and processes and will use them to represent and analyze relationships
among variable quantities and to solve problems.
|
Standard 13 - Algebra - Grades K-2
Overview
Students can develop a strong understanding of algebraic concepts
and processes from consistent experiences in classroom activities
where a variety of manipulatives and technology are used. The key
components of this understanding in algebra, as identified in the K-12
Overview, are: patterns, unknown quantities, properties,
functions, modeling real-world situations, evaluating
expressions and solving equations and
inequalities.
Students begin their study of algebra in grades K-2 by learning
about the use of pictures and symbols to represent variables. They
look at patterns and describe those patterns. They begin to
look for unknown numbers in connection with addition and
subtraction number sentences. They model the relationships
found in real-world situations by writing number sentences that
describe those situations. At these grade levels, the study of
algebra is very much integrated with the other content standards.
Children should be encouraged to play with concrete materials,
describing the patterns they find in a variety of ways.
People tend to learn by identifying patterns and generalizing or
extending them to some conclusion (which may or may not be true). A
major emphasis in the mathematics curriculum in the early grades
should be the opportunity to experience numerous patterns. The
development of algebra as a language should build on these
experiences. The ability to extend patterns falls under Standard 11
(Patterns and Functions), but having students communicate their
reasoning is also an algebra expectation. Initially, ordinary
language and concrete materials should be used for communication. As
students grow older and patterns become more complex, students should
develop the ability to use tables and pictures or symbols (such as
triangles or squares) to represent numbers that may change or are
unknown (variable quantities).
The primary grades provide an ideal opportunity to lay the
foundation for the development of the ability to represent situations
using equations or inequalities (open sentences) and solving
them. Students can be asked to communicate or represent relationships
involving concrete materials. For example, two students might count
out eight chips and place them on a mat. One of the students then
places a margarine tub over some of the counters and challenges the
other student to figure out how many chips are hidden under the tub.
A more complex situation might involve watching the teacher balance a
box and two marbles with six marbles. The students draw a picture of
the situation, and try to decide how many marbles would balance the
box by physically removing two marbles from each side of the balance.
In a problem involving an inequality, students might be asked to find
out how many books Jose has if he has more than three books but fewer
than ten. Situations from the classroom and the students' real
experiences should provide ample opportunities to construct and solve
such open sentences.
As operations are developed, students need to examine
properties and make generalizations. For example, giving
students a set of problems which follow the pattern 3 + 4, 4
+ 3, 1 + 2, 2+1, etc. should provide the opportunity
to develop the concept that order does not affect the answer when
adding (the commutative property). After students understand that
these properties are not necessarily true for all operations (e.g.,
5 - 2 is not equal to 2 - 5),
the teacher should mention that the properties are important enough to
be given names. However, the focus of this work should be on using
the properties of operations to make work easier rather than on
memorizing the properties and their names.
Students in grades K-2 spend a great deal of time developing
meaning for the arithmetic operations of addition, subtraction,
multiplication, and division. As they work toward understanding these
concepts, they focus on developing mathematical models for
concrete problem situations. The number sentences that they write to
describe these problem situations form a foundation for more
sophisticated mathematical models.
Standard 13 - Algebra - Grades K-2
Indicators and Activities
The cumulative progress indicators for grades K-2 appear below in
boldface type. Each indicator is followed by activities which
illustrate how it can be addressed in the classroom in kindergarten
and in grades 1 and 2.
Experiences will be such that all students in grades K2:
1. Understand and represent numerical situations
using variables, expressions, and number sentences.
- Students represent a problem situation with an open
sentence. For example: If there are 25 students in the
class and Marie brought 26 cookies for snack, how many will be left
over? (26 - 25 = ?) Another example might be:
We have 10 cups left in the package and there are 25
children in the class, so how many more cups do we need to
get?
(10 + ? = 25)
- Students read The Doorbell Rang by Pat Hutchins.
They act out the story and realize that many different combinations of
students can share 12 cookies equally.
- Students make a table relating the number of people and
the number of eyes. They use a symbol such as a stick figure to
represent the number of people and a cartoon drawing of an eye to
represent the number of eyes and then express the relationship between
them.
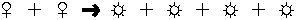
2. Represent situations and number patterns with concrete
materials, tables, graphs, verbal rules, and number sentences,
and translate from one to another.
- Students in groups are given a container to which they add
water until its height is 5 centimeters, measured with Cuisennaire
rods. They add marbles to the container until the height of the water
is 6 centimeters. They continue adding marbles, recording each time
the number of marbles it takes to raise the water level one
centimeter. They describe the relationship between the number of
marbles added and the height of the water.
- In regular assessment activities, students look at a
series of pictures which form a pattern. They draw the next shape,
describe the pattern in words, and explain why they chose to draw that
shape.
- Using a calculator, students play Guess My Rule.
The lead student enters an expression such as 5+4 and presses
the = key; she shows only the answer to her partner. The
second student tries to guess the rule by entering different numbers,
one at a time, pressing the = key after each number. The
calculator, after each = is pressed, should show the sum
of the entered number and the second addend (in this case, 4). (Some
calculators perform this function differently; see the user's
manual for instructions.) When the second student thinks she knows the
pattern (in this case, adding 4), she makes a guess. The
pattern is written in words and then as a rule using a picture or
symbol forthe variable (the number which the second student
enters).
- Placing four differentcolored cubes in a can, students
predict which color would be drawn out most often if each child draws
one cube without looking. The teacher helps the students keep track
of their results by making a chart with the colors on the horizontal
axis and the number of times a color is drawn on the vertical axis.
As students select cubes, an "x" is placed above the color
drawn, forming a frequency diagram. After several turns, the students
describe the patterns they see in the graph.
- Students read Ten Apples Up on Top! by
Theo Le Sieg and discuss the mathematical comparisons and equations
that appear in the story.
3. Understand and use properties of operations
and numbers.
- Students are given five
computational problems to solve. They are permitted to use the
calculator on only two of them. Two of the problems are related to
another two by operation properties (e.g., 3 + 2 and 4 +
6 are related to 2 + 3 and 6 + 4 by the commutative
property) and the last involves a property of number such as adding
0. Students share their thought processes in a follow up
discussion.
- The second grade teacher has a box containing slips of
paper with open sentences such as 25 - 8 =
 or 15
+
or 15
+
 = 23. Students draw out a slip and tell or write a story which
would involve a situation modeled by the sentence.
= 23. Students draw out a slip and tell or write a story which
would involve a situation modeled by the sentence.
- Students discover that, since the order of the numbers
when adding them is not important, they can solve a problem like 3
+ 8 by starting with 8 and counting up 3, as well as by starting
with 3 and counting up 8.
- In their math journals, students write their
reactions to the following situation:
Sally just used her calculator to find out that 324 + 486 was
equal to 810. In another problem, she must find the answer to
486 + 324. What should she do? Why?
4. Construct and solve open sentences (example:
3 +
 = 7) that describe reallife situations.
= 7) that describe reallife situations.
- Kindergarten students play the hide the pennies
game. The first player places a number of pennies (say 7) on the
table and lets the other player count them. The first player covers
up a portion of the pennies, and the second player must determine how
many are covered. They may represent the situation with markers or
pictures to help them. Some second-grade students are ready to write
a number sentence that describes the situation.
- Students are given a bag with Unifix cubes. They are told
that the bag and 2 cubes balance 7 cubes. They use a balance scale to
find how many cubes are in the bag.
References
-
Hutchins, Pat. The Doorbell Rang. Mulberry Books,
1986.
Le Sieg, Theo. Ten Apples Up on Top! New York, NY:
Random House, 1961.
On-Line Resources
-
http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/
The Framework will be available at this site during Spring
1997. In time, we hope to post additional resources relating to this
standard, such as grade-specific activities submitted by New Jersey
teachers, and to provide a forum to discuss the Mathematics
Standards.
|
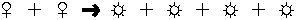
 or 15
+
or 15
+