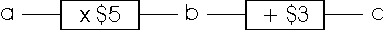STANDARD 13 - ALGEBRA
Standard 13 - Algebra - Grades 3-4OverviewStudents can develop a strong understanding of algebraic concepts and processes from consistent experiences in classroom activities where a variety of manipulatives and technology are used. The key components of this understanding in algebra, as identified in the K-12 Overview, are: patterns, unknown quantities, properties, functions, modeling real-world situations, evaluating expressions and solving equations and inequalities. In grades K-2, students use pictures and symbols to represent variables, generalize patterns verbally and visually, and work with properties of operations. Although the formality increases in grades 3 and 4, it is important not to lose the sense of play and the connection to the real world that were present in earlier grades. As much as possible, real experiences should generate situations and data which students attempt to generalize and communicate using ordinary language. Students should explain and justify their reasoning orally to the class and in writing on assessments using ordinary language. When introducing a more formal method of communicating, such as the language of algebra, it is helpful to revisit some of the situations used in previous grades. Since algebra is the language of patterns, the mathematics curriculum at this level needs to continue to focus on patterns. The use of letters to represent unknown quantities should gradually be introduced as a replacement for pictures and symbols. The use of function machines permits the introduction of letters without the need to move to formal symbolic algebra. Since they have had the opportunity to experience real function machines such as the calculator or a gum bank, where one penny yields two pieces of gum, the notation of function machines should make sense. 
Here the box is thought of as the function machine times 2 which takes in a number "a" and produces a number "b" which is twice "a." Students can use such symbols to communicate their generalization of patterns. They put two or more machines together making a composite function; for example, they can follow the times 2 machine with an add 3 machine. They determine not only what each input produces but also what input would produce a given output.
Students in grades 3 and 4 should continue to use equations and inequalities to represent real situations. While variables can be introduced through simple equations such as 35 ÷ n = 5, students should be viewing variables as place holders similar to the open boxes and pictures they have already used. At these grade levels, they need not use variables in more complicated situations. Given a situation such as determining the cost of each CD if 5 of them plus $3 tax is $23, they should be permitted to represent it in whatever way they feel comfortable. Students should be able to use, explain, and justify whatever method they wish to solve equations and inequalities. Some may continue to use concrete materials for some situations; they might count out 23 counters, set aside 3 for the tax, and divide the remainder into 5 equal piles of 4. Others might try different numbers until they find one that works. Some students may write 23 - 3 = 20 and 20 ÷ 5 = 4. Still others may want to relate this to function machines and figure out what had to go in for $23 to come out. It is important for students to see the diversity of approaches used and to discuss their interrelationships. Students should continue to examine the properties of operations and use them whenever they would make their work easier. There are some excellent opportunities for providing a foundation for algebraic concepts in these grades. For example, explaining twodigit multiplication by using the area of a rectangle (see figure below illustrating 13 x 27) provides the student with a foundation for multiplication of binomials, the distributive property, and factoring. While the teacher at this grade level should focus on the development of the multiplication algorithm, the teacher of algebra several years later will be able to build on this experience of the student. 
Standard 13 - Algebra - Grades 3-4Indicators and ActivitiesThe cumulative progress indicators for grade 4 appear below in boldface type. Each indicator is followed by activities which illustrate how it can be addressed in the classroom in grades 3 and 4. Building upon knowledge and skills gained in the preceding grades, experiences in grades 3-4 will be such that all students: 1. Understand and represent numerical situations using variables, expressions, and number sentences.
2. Represent situations and number patterns with concrete materials, tables, graphs, verbal rules, and number sentences, and translate from one to another.
3. Understand and use properties of operations and numbers.
4. Construct and solve open sentences (example: 3 + _ = 7) that describe reallife situations.
References
On-Line Resources
|
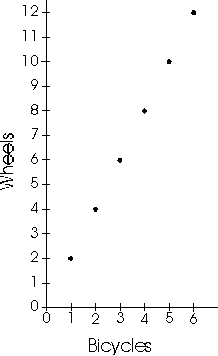 Students should continue to communicate their generalizations
of patterns through ordinary language, tables, and concrete materials.
Graphs should be introduced as a method for quickly and efficiently
representing a pattern or function. They should develop graphs which
represent real situations and be able to describe patterns of a
situation when shown a graph. For example, when given the graph at
the right which shows the relationship between the number of bicycles
and wheels in the school yard, they should be able to describe the
relationship in words.
Students should continue to communicate their generalizations
of patterns through ordinary language, tables, and concrete materials.
Graphs should be introduced as a method for quickly and efficiently
representing a pattern or function. They should develop graphs which
represent real situations and be able to describe patterns of a
situation when shown a graph. For example, when given the graph at
the right which shows the relationship between the number of bicycles
and wheels in the school yard, they should be able to describe the
relationship in words.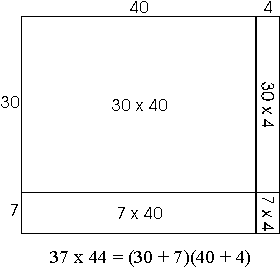 When the students are introduced to twodigit by twodigit
multiplication, they begin with a problem of finding the area of a
rectangular field which is 37 feet by 44 feet. They know they need to
multiply the numbers to find the area, but they don't know how to
multiply without calculators. The teacher draws a rectangle and uses
a line to divide the width into two regions which are 30 feet and 7
feet. She does the same with the length, cutting it into lengths 40
feet and 4 feet. This divides the rectangle into four smaller
rectangles (30×40, 30×4, 7×40,
7×4) all of which are multiplications the students can
do.
When the students are introduced to twodigit by twodigit
multiplication, they begin with a problem of finding the area of a
rectangular field which is 37 feet by 44 feet. They know they need to
multiply the numbers to find the area, but they don't know how to
multiply without calculators. The teacher draws a rectangle and uses
a line to divide the width into two regions which are 30 feet and 7
feet. She does the same with the length, cutting it into lengths 40
feet and 4 feet. This divides the rectangle into four smaller
rectangles (30×40, 30×4, 7×40,
7×4) all of which are multiplications the students can
do.