Students can develop a strong understanding of algebraic concepts and processes from consistent experiences in classroom activities where a variety of manipulatives and technology are used. The key components of this understanding in algebra, as identified in the K-12 Overview, are: patterns, unknown quantities, properties, functions, modeling real-world situations, evaluating expressions and solving equations and inequalities.

It is important that students continue to have informal algebraic experiences in grades 5 and 6. Students have previously had the opportunity to generalize patterns, work informally with open sentences, and represent numerical situations using pictures, symbols, and letters as variables, expressions, equations, and inequalities. At these grade levels, they will continue to build on this foundation.

Algebraic topics at this level should be integrated with the development of other mathematical content to enable students to recognize that algebra is not a separate branch of mathematics. Students must understand that algebra is an expansion of the arithmetic and geometry they have already experienced and a tool to help them describe situations and solve problems.

Students should use algebraic concepts to investigate situations and solve interesting mathematical and real world problems. There should be numerous opportunities for collaborative work. Since algebra is the language for describing patterns, students should have regular and consistent opportunities to discuss and explain their use of these concepts. They should write generalizations of situations in words as well as in symbols. To provide such opportunities, the activities should move from a concrete situation or representation to a more abstract setting. Students at this level can begin using standard algebraic notation to represent known and unknown quantities and operations. This should be developed gradually, moving them from the previous symbols in such a way that they can appreciate the power and elegance of the new notation.

Students need to learn how variables are different from numbers (a variable can represent many numbers simultaneously, it has no place value, it can be selected arbitrarily) and how they are different from words (variables can be defined in any way we want and can be changed without affecting the values they represent). Students need to see variables (letters) used as names for numbers or other objects, as unknown numbers in equations, as a range of unknown values in inequalities, as generalizations in pattern rules or formulas, and as characteristics to be graphed (independent and dependent variables).

An algebraic expression involves numbers, variables, and operations such as 2b, 3x - 2, or c - d. In fifth and sixth grade, students should begin to become familiar with the common notational shortcut of omitting the operation sign for multiplication, so that when b=3, 2b equals 6 and not 23. Thus they recognize that there are slightly different rules for reading expressions involving variables than those involving only numbers.

Students in grades 5 and 6 should focus on understanding the role of the equal sign. Because it is so often used to signal the answer in arithmetic, students may view it as a kind of operation sign - a "write the answer" sign. They need to come to see its role as a relation sign, balancing two equal quantities. Students should develop the ability to solve simple linear equations using manipulatives and informal methods. With the appropriate background, students at grades 5 and 6 have the ability to find the solution of an equation, such as 7 for x+5=12, whether they use manipulatives, a graph, or any other method. It is imperative that in the discussion of the solution of an equation, the many methods in obtaining that solution are described.

Students in grades 5 and 6 should use concrete materials, such as algebra tiles, to help them develop a visual, geometric understanding of algebraic concepts. For example, students can represent the expression 3x - 2 by using three strips and two units. They should make graphs on a rectangular coordinate system from data tables, analyze the shape of the graphs, and make predictions based on the graphs. Students should have opportunities to plot points, lines, geometric shapes, and pictures. They should use variables to generalize the formulas they develop in studying geometry (e.g., p = 4s for a square or A = l×w for a rectangle). Students should be able to describe movements of objects in the plane through horizontal and vertical slides (translations). They should experiment with probes which generate the graphs of experimental data on computers or graphing calculators. The majority of this work will be with graphs that are straight lines (linear functions), but students should have some experience seeing other shapes of graphs as well; in particular, when dealing with real data and probes, many times the graph will not be linear.

The cumulative progress indicators for grade 8 appear below in boldface type. Each indicator is followed by activities which illustrate how it can be addressed in the classroom in grades 5 and 6.

Building upon knowledge and skills gained in the preceding grades, experiences in grades 5-6 will be such that all students:

5. Understand and use variables, expressions, equations, and inequalities.

• Students find the perimeter of one square, two squares connected along an edge, three squares connected along their edges, and so forth, as shown below. The length of one side of a square is assumed to be one unit.
  

  They make a table of values and use it to determine a function rule which describes the pattern. They understand the rule P = 2×s + 2, and use it to predict the perimeter of ten squares.

• Students write a Logo program to draw a rectangle of any dimensions using the variables :LENGTH and :WIDTH.

• In a health unit, students are studying the dietary needs for maintaining healthy bodies. The teacher provides guidelines for the maximum amounts of fat and cholesterol at any meal. Each group of students chooses two foods for a meal. They determine the fat content per unit of each of the foods and the cholesterol amount per unit and make inequalities which relate these unit values, the number of units, and the given maximum amounts. The students determine possible combinations of the amounts of the two foods whose fat and cholesterol would still be acceptable. The teacher uses a function graphing computer program or graphing calculator to represent visually the acceptable amounts.

6. Represent situations and number patterns with concrete materials, tables, graphs, verbal rules, and standard algebraic notation.

• Each group of students is given a Mr. or Mrs. Grasshead (i.e., a sock filled with dirt and grass seed which sits in a dish of water). They create a name for their grasshead and begin a diary, recording the number of days that have passed and the height of the grass. At the end of specified time periods, they discuss the changes in the height, the average rate of change over the time period, and the overall behavior of the grass growth. Each group makes a graph of height versus the number of days. The students note whether the graph is close to a straight line.

• Students find the number of tiles around the border of a floor 10 tiles long and 10 tiles wide by looking at smaller square floors, making a table, and identifying a pattern. They describe their pattern in words and, with assistance from the teacher, develop theexpression (4 × n) + 4 for the number of border tiles needed for an n × n floor.

• Students play Guess My Rule by suggesting input and having the rule-maker (the teacher or a student) put the corresponding output into a table like this one:

  Input	Output
  3	9
  1	5
  16	35
  .	.
  .	.
  .	.
  n	2n+3

  Students should always be challenged to show they understand the rule by filling in the last row for an input of n. Partially filled-in Guess My Rule tables are also a good assessment technique to evaluate students' inductive reasoning power and their ability to use standard algebraic notation to express relationships.

• Students use play money to act out the following situation and solve the problem.

  A man wishes to purchase a pair of slippers marked $5. He gives the shoe salesman a $20 bill. The salesman does not have change for the bill so he goes to the pharmacist next door and gets a $10 and two $5 bills. He gives the customer his change and the man leaves. The pharmacist enters shortly after and complains the $20 was counterfeit. The shoe salesman gives her $20 and gives the counterfeit bill to the FBI. How much did the shoe salesman lose?

• Students place 8 two-color chips in a paper cup and toss them ten times, recording the number of red and yellow sides showing on each toss. For each red chip that shows, they lose $1. For each yellow, they win $1. For each toss, the students write a number sentence that shows their win or loss for that toss. For example, after tossing 3 yellows and 5 reds, their sentence would read 3 - 5 = -2. Afterwards, the students look for patterns in the number sentences that they have written. They discuss these patterns and then write about them in their notebooks.

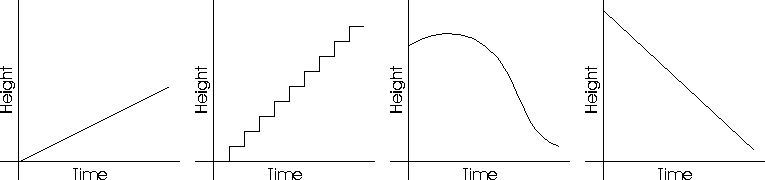
• In both classroom and assessment situations, students interpret simple non-numeric graphs and decide what kinds of relationships they demonstrate. For example: Which of the following graphs would show the relationship between the height of a flag and time as a boy scout raised the flag on a flagpole?

  

• Students work through the Powers of the Knight lesson that is described in the Introduction to this Framework. They learn that doubling the number of coins on consecutive squares of a chessboard results in a rapidly increasing sequence of numbers - the powers of 2.

• Students read Anno's Mysterious Multiplying Jar by Mitsumasa Anno and try to analyze and represent the numerical patterns shown using variables.

7. Use graphing techniques on a number line to model both absolute value and arithmetic operations.

• Students use number lines to demonstrate addition of integers. They point to the number representing the amount currently in the bank and then slide their finger in the appropriate direction (right for deposits and left for withdrawals) over the distance indicated by the second amount. As they slide their finger, they use arrows to track their movements over the number line, and the teacher keeps track of the operations using positive and negative integers. Through this dual representation, students begin to understand the relationship between the addition of integers and movement along the number line.

• Students are given a variety of objects whose dimensions they must determine. They are given a number line marked from 5 to 27 to simulate a broken yardstick. Students work in pairs to develop a process for determining the lengths of each of the objects to the nearest unit. After they have a workable method and have written an explanation of it in their journal, the teacher replaces the tape with another which is marked from 10 to 10. The students repeat their effort. This process helps them develop an understanding of subtraction of integers and the relationship between the operation of subtraction and distance on the number line.

• Addition and subtraction of signed numbers is explored using two-colored disks and a number line. Red is used to represent positive numbers and yellow is used to represent negative numbers. When given a problem such as -3 + 5 the students place 3 yellows and 5 reds on the table. They pair up as many red and yellow disks as they can and remove them from the table. In the case of the example, 3 red and yellow disks would be paired and removed, leaving 2 red disks which represents the sum, +2.

8. Analyze tables and graphs to identify properties and relationships.

• Students use tables or two-color chips to help them solve the following problem: A classroom has 25 lockers in a row. The first person to enter the room opened every locker. The second person closed every other locker beginning with the second locker. The third person started with the third locker and changed every third locker from open to closed or closed to open. This continued until 25 people had passed through the room. Which lockers would be open after the 25th person walked into the room?

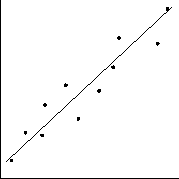• A plastic rectangular shape is exhibited on the overhead. The lengths of both sides of the image, and the distance from the screen to the overhead are measured. The overhead is moved and the process is repeated so that measurements are taken at six to ten different distances. One group of students is responsible for determining the relationship between the distance from the screen and the length of one side of the image. A second group is responsible for studying the relationship between the distance from the screen and the area of the image. Each group makes a scatterplot of its data and eyeballs a line of best fit using a piece of spaghetti. They then use the graph to answer questions about the relationship between distance and length or distance and area. They also develop a summary statement describing the relationship.

• Students make pendulums using strings of length 64, 32, 16, and 8 cm with a washer at one end and a screw eye or ruler at the other. The strings are swung from a constant height and the number of swings in 30 seconds is recorded. A graph is made plotting the number of swings against the string length. Students study the results and determine if there might be a pattern they could continue. They attempt to answer questions such as: Will the number of swings ever reach zero? (This activity is a good one to repeat at later grades since the relationship appears linear but when very short lengths and very long lengths are used, it becomes clear that it is actually a quadratic relationship.)

• Students are given the times of the Olympic 100meter freestyle swimming winners both in the men's event and the women's event. Using different colors for the two genders, they produce a scatterplot and use a piece of spaghetti to eyeball a line of best fit for each set of data. They use their lines to determine times in the years not given (when no Olympics were held) and to predict times in the years beyond those they were given. They also determine if the data supports the assertion that the women will some day swim as fast as the men and predict from their lines when that would happen.

9. Understand and use the rectangular coordinate system.

• Students are paired to play a game similar to battleship in which they attempt to determine where the two lines their opponent has drawn intersect. Both students draw axes which go from -10 to 10 in both the x and ydirections. They sit so that neither can see the other's paper. The first player draws two lines which intersect at a point with integer coordinates and colors the four regions different colors. The second player gives the coordinates of a point. The first player responds with the color of the region the point is in, or that the point is on a line, or that it is the point! The second player keeps a record of his guesses on his axes and continues guessing until the chosen point is determined.

• Students keep track of the high and low temperatures for a month in two different colors on a graph. The horizontal axis represents the day of the month and the vertical axis represents the temperature. At the end of the month, they connect the points making two broken-line graphs. They use their graphs to discuss the temperature variations of that month and to determine the overall "high" and "low" for the month.

• Students consider what happens if they start with two bacteria and the number of bacteria doubles every hour. They make a table showing the number of hours that have passed and the number of bacteria and then plot their results on a coordinate graph.

• Students draw broken-line pictures in a cartesian plane and identify the coordinates of critical points in the pictures. Their partners attempt to re-create the picture using the coordinates of the critical point and verbal descriptions of how the critical points should be connected.

10. Solve simple linear equations using concrete, informal, and graphical methods, as well as appropriate paper-and-pencil techniques.

• Students use algebra tiles to solve an equation. For example, they represent the equation 3x + 2 = 5x by placing three strips and two units on one side of a picture of a balance beam and five strips on the other side. They decide that the balance will stay even if they take the same number of objects off both sides, so they take three strips off both sides and have two units balanced with two strips. Then they correctly decide that 1 unit must balance one strip.

• Students want to use their class fund as a donation to a town in Missouri devastated by the summer floods. They agree that each of the 26 students in the class is going to contribute 25 cents a week. The fund already contains $7. The students develop the expression $6.50×W+$7 as the amount of money in the fund at the end of W weeks. The teacher asks them how much they would like to send to the town, and the students agree on $100. The teacher then asks them to write an equation which would say that the amount of money after W weeks was $100. The students write $6.50×W + $7 = $100. Finally, the students try a number of different strategies for finding out what W should be. Some of the students use calculators in a guessandcheck method. Some students go to the computer and use a spreadsheet to generate the amounts for different weeks until the total is more than $100. Others express the relationship as a composite function using function machines and then use the inverse operations to subtract $7 and then divide by $6.50. They use their calculators to carry out the division. The teacher discusses all these methods and introduces the traditional algebraic shorthand method for solving the problem.

11. Explore linear equations through the use of calculators, computers, and other technology.

• Using a motion sensor connected to a graphing calculator or computer, the class experiments with generating graphs which represent the distance from the sensor against time. They discover that if they walk at a fixed rate the graph is a straight line. They try walking away from the sensor at different fixed rates of speed to determine what effect the speed has on the line. They start at different distances from the sensor to see the effect that has. They try walking toward the sensor and standing still. Students discuss the relationships between the lines they are generating and the physical activity they do. As an assessment, the teacher has individual students walk so as to generate a straight line. The students are then asked to write in their journals what someone would have to do to produce a line which was less steep. After closing their journals, individual students are provided an opportunity to verify their conclusions using the graphing calculator.

• After measuring several students' heights and the length of the shadows they produce, the data is entered in a spreadsheet, computerized statistics package, or graphing calculator. A scatterplot is formed from the data and the students see that the plot is approximately linear. The technology is used to produce a line of best fit which the class uses to determine heights of unknown objects (such as a flagpole) and the length of the shadow of objects with known heights.

12. Investigate inequalities and nonlinear equations informally.

• Students explore patterns involving the sums of the odd integers (1, 1+3, 1+3+5, ...) byusing small squares to make Ls to represent each odd number and then nesting the Ls. They make a table that shows how many Ls are nested and the total number of squares used.
  

  They look for a pattern that will help them predict how many squares will be needed if 10 Ls are nested (i.e., if the first 10 odd numbers are added together). They make a prediction and describe the basis for their prediction (e.g., when you added the first 3 odd numbers, and placed the three Ls together, they formed a square that was three units on a side, so when you add the first 10 odd numbers, that should make a square that is ten units on a side and whose total area is 100 squares.) They share their solution strategies with each other and develop an expression that can be used to find the sum of the first n odd numbers (i.e., n × n).

• Students set up a table listing the length of the sides of various squares (x) and their areas (y). Some students use the centimeter blocks to help them find the values. The teacher completes a table of values in a function graphing computer package on the class computer which has an LCD panel for overhead projection or on an overhead version of a graphing calculator. When the students have finished completing the table, the teacher turns on the overhead and displays her table. The students check their answers and ask questions. The teacher graphs the data on the computer or calculator, and the students use the graph to answer questions such as If the side was 3.5 cm, what would the area be? and If the area was 60 square centimeters, what would the side be? The teacher uses the trace function to identify the points being discussed.

• Students explore inequality situations such as: I have $150. How many more weeks would I need to save my $15 allowance to buy a stereo that costs $200? They represent the relationship as an inequality, both in words and in symbols, and use play money, base ten blocks, graphs, or trial and error to solve the problem.

13. Draw freehand sketches of, and interpret, graphs which model real phenomena.

• Students keep track of how far they are from home during one specified day. They draw a graph which represents the distance from home against the time of day and write an explanation of their graph in relation to their actual activities on that day.

• Students are presented with a graph representing a student's monthly income from performing lawn care for people over the past year. The graph shows no income during the months of November, December, and March. They write a story which explains the behavior of the graph in terms of the need for services over the course of the year.

References

Anno, Mitsumasa. Anno's Mysterious Multiplying Jar. Philomel Books, 1983.

On-Line Resources

http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/

The Framework will be available at this site during Spring 1997. In time, we hope to post additional resources relating to this standard, such as grade-specific activities submitted by New Jersey teachers, and to provide a forum to discuss the Mathematics Standards.