Approximation by the conditional mean bandwidth. In this paper, the state information upon which we condition will be either the current level of each source or the current level and age (current time) in that level of each source. No state from the within level process is assumed. Conditional on that state information, we can compute the probability that each source will be in each possible level at any time in the future, from which we can calculate the conditional mean and variance of the aggregate required bandwidth by adding.
The Lindeberg-Feller central limit theorem (CLT) for non-identically-distributed summands can be applied to generate a normal approximation characterized by the conditional mean and conditional variance; see p. 262 of Feller [13]. For the normal approximation we must check that the aggregate is not dominated by only a few sources.
Let B(t) denote the (random) aggregate required bandwidth at time t, and let I(0) denote the (known deterministic) state information at time 0. Let (B(t) | I(0)) be a random variable with the conditional distribution of B(t) given the information I(0). By the CLT, the normalized random variable
| |
(2) |
Since the conditional mean alone tends to be very descriptive, we use the approximation
| |
(3) |
Given that our approximation is the conditional mean, and given that our state
information does not include the state of the within-level variation process,
the within-level variation process plays no role because it has zero mean.
Let i index the source.
Since the required bandwidths need not have integer
values, we index the level by the integer
j, ![]() , and
indicate the associated required bandwidths
in the level by bji.
Hence, instead of (1),
the required bandwidth for source i can be expressed as
, and
indicate the associated required bandwidths
in the level by bji.
Hence, instead of (1),
the required bandwidth for source i can be expressed as
| |
(4) |
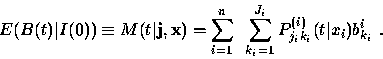 |
(5) |
From (5), we see that we need to compute the
conditional distribution of the level, i.e., the probabilities
Pjk(i) (t|x), for each source i.
In this section we show how to compute these conditional probabilities.
We consider a single source and assume that its required
bandwidth process is a semi-Markov process (SMP).
(We now have no within-level variation process.)
We now omit the superscript i. Let L(t) and B(t) be the level and required
bandwidth, respectively, at time t as in (4). The process ![]() is assumed to be an SMP, while the process
is assumed to be an SMP, while the process ![]() is a function of an SMP, i.e., B(t) = bL(t), where bj is the
required bandwidth in level j. If
is a function of an SMP, i.e., B(t) = bL(t), where bj is the
required bandwidth in level j. If ![]() for
for ![]() , then
, then
![]() itself is an SMP, but if bj = bk for some
itself is an SMP, but if bj = bk for some
![]() , then in general
, then in general ![]() is not an SMP.
is not an SMP.
Laplace transform analysis. Let A(t) be the age of the level holding time at time t. We are interested in calculating
| |
(6) |
| |
(7) |
| |
(8) |
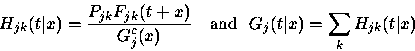 |
(9) |
| |
(10) |
| |
(11) |
| |
(12) |
Theorem 6812
The transient probabilities for a single SMP source have the matrix of Laplace transforms
| |
(13) |
| |
(14) |
Proof.
In the time domain, condition on the first transition.
For ![]() ,
,
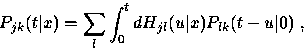
![]()
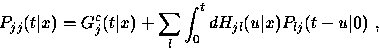
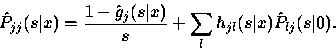
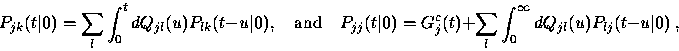
P(t|0) = D(t) + Q(t) * P(t|0)
where * denotes convolution, and (14) holds.
To compute the LT ![]() , we only need the LSTs
, we only need the LSTs
![]() and
and ![]() associated with the basic
holding-time cdf's Fjk and Gj. However, to compute
associated with the basic
holding-time cdf's Fjk and Gj. However, to compute
![]() , we also need to compute
, we also need to compute ![]() and
and
![]() , which require computing the LSTs of the
conditional cdf's Hjk(t|x) and Gj(t|x) in (9).
The LSTs of these conditional cdf's are often easy to obtain
because some cdf's inherit their structure upon conditioning.
For example, this is true for phase-type, hyperexponential and
Pareto distributions. Moreover, other cdf's can be approximated
by hyperexponential or phase-type cdf's; see Asmussen, Nerman and Olsson
[2] and Feldmann and Whitt [12].
If the number of levels is not too large, then it will not be
difficult to compute the required matrix inverse (I - q(s))-1
for all required s. Note that, because of the probability
structure, the inverse is well defined for all complex s with
, which require computing the LSTs of the
conditional cdf's Hjk(t|x) and Gj(t|x) in (9).
The LSTs of these conditional cdf's are often easy to obtain
because some cdf's inherit their structure upon conditioning.
For example, this is true for phase-type, hyperexponential and
Pareto distributions. Moreover, other cdf's can be approximated
by hyperexponential or phase-type cdf's; see Asmussen, Nerman and Olsson
[2] and Feldmann and Whitt [12].
If the number of levels is not too large, then it will not be
difficult to compute the required matrix inverse (I - q(s))-1
for all required s. Note that, because of the probability
structure, the inverse is well defined for all complex s with
![]() . To illustrate with an important simple example,
we next give the explicit formula for an on-off source.
. To illustrate with an important simple example,
we next give the explicit formula for an on-off source.
Example 2.1. Suppose that we have an on-off source, i.e., so that there are two states with transition probabilities P12 = P21 = 1 and holding time cdf's G1 and G2. From (9) or by direct calculation,
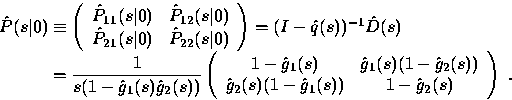 |
(15) |
| |
(16) |
| |
(17) |
We now determine the mean, second moment, and variance of
the bandwidth process of a general multi-level source as a function of
time. It is elementary that
| |
(18) |
Finally, we consider the aggregate bandwidth associated with n sources. Again let a superscript i index the sources. The conditional aggregate mean and variance are
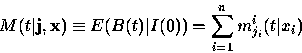 |
(19) |
![\begin{displaymath}
V(t\vert{\bf j}, {\bf x}) \equiv Var (B(t)\vert I(0)) = \dis...
...\sum^n_{i = 1}
[v^i_{j_i} (t\vert x_i)+w^i_{j_i}(t\vert x_i)],\end{displaymath}](img50.gif) |
(20) |
It is significant that we can calculate the conditional aggregate mean at any time t by performing a single inversion. We summarize this elementary but important consequence as a theorem.
Theorem 6869
The Laplace transform of the n-source conditional mean aggregate required bandwidth as a function of time is
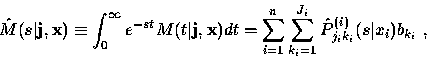 |
(21) |
Unlike for the aggregate mean, for the aggregate variance we evidently
need to perform n separate inversions to calculate viji
(t|xi) for each i and then add
to calculate ![]() in (23).
(We assume that the within-level variances wiji(t|xi), if included,
are specified directly).
Hence, we suggest calculating only the conditional mean on line for control,
and occasionally calculating the conditional variance off line to evaluate
the accuracy of the conditional mean.
in (23).
(We assume that the within-level variances wiji(t|xi), if included,
are specified directly).
Hence, we suggest calculating only the conditional mean on line for control,
and occasionally calculating the conditional variance off line to evaluate
the accuracy of the conditional mean.