The matrix inverse (I-q(s))-1 is a compact representation for the
series ![]() .For P(t|x), it captures the possibility of any number of
transitions up to time t.
However, if the levels are relatively long in the time
scale relevant for control, then the mean for times t of interest will only be
significantly affected by a very few transitions.
Indeed, often only a single transition need be considered.
.For P(t|x), it captures the possibility of any number of
transitions up to time t.
However, if the levels are relatively long in the time
scale relevant for control, then the mean for times t of interest will only be
significantly affected by a very few transitions.
Indeed, often only a single transition need be considered.
The single-transition approximation is obtained by making the Markov chain absorbing after one transition. Hence, the single-transition approximation is simply
| |
(22) |
Alternatively, we can develop a two-transition approximation. (Extensions to higher numbers are straightforward.) Modifying the proof of Theorem 2.1 in a straightforward manner, we obtain
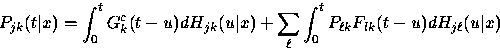 |
(23) |
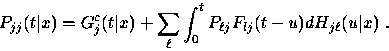 |
(24) |
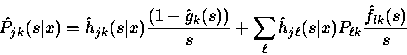 |
(25) |
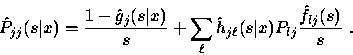 |
(26) |
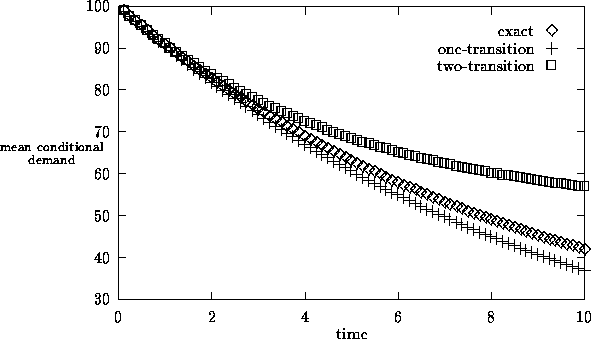
Example 3.1. To illustrate how the two approximations compare to the exact conditional mean, we give a numerical example. We consider a single source with four levels. The transitions move cyclically through the levels: P12 = P23 = P34 = P41 = 1. The level holding-time ccdf's are:
The level bandwidths are b1 = b3 = 100 and b2 = b4 = 0. Suppose that we start in level 1 with an age of 8. From the form of G1c (t), we see that the conditional level-1 holding-time ccdf G1c (t|x) is then approximately e-0.1t. Hence the first two mean level holding times are approximately 10. Hence we might consider the one-transition and two-transition approximations in the interval [0,10]. The two approximations are compared to the exact value of the conditional mean in Figure 1. (All are computed by numerical transform inversion.) The approximations are very good up to t = 1 or 2, but they start to degrade by t = 10. The two-transition approximation performs not so well for larger t because the actual holding time in level 3 is likely to be quite short. More generally, our experience is that the one-transition and two-transition approximations tend to perform quite satisfactorily if the mean level holding times in the first few levels are substantially larger than the times t of interest. In this example the approximations are quite good in the interval [0,1].
 |